簡単な仮想計算機を作ろう(準備編):Javaでコンパイラの基礎を理解する(2)(1/2 ページ)
教育界、技術者コミュニティでJava言語の教育と啓蒙に長年携わってきた筆者が、Javaを通してコンパイラの仕組みを分かりやすく紹介する。(編集部)
仮想計算機もどき
前回はコンパイラを自作する意義と基本構成について述べましたが、今回はいよいよコンパイラ作成の準備に取り掛かります。
コンパイラを作成するには、ターゲットとなる計算機が必要です。このため、コンパイラに関する専門書では、具体的なCPUと、そのCPUがサポートする命令セットとを決めて解説している場合が多いのです。この連載では基本的な話から進めますので、スタックを使った仮想計算機を作成して使うことにします。
「仮想計算機」と聞くと期待感が高くなると同時に、難しそうと思われるかもしれません。しかし実際は、「仮想計算機もどき」といった方がいいぐらいの簡単なものを対象とします。実際のコードを見ると、それほど難しくはありませんから、安心してください。
また、スタックを使って四則演算を含む計算式の結果を簡単に求めることができますが、そのためには、後置記法といわれる式の表現方法について理解する必要があります。これについても解説をします。
後置記法による式の表現
最初に、今回の仮想計算機ではどんな計算ができるようにするか、について簡単に述べておきます。計算自体は非常に単純ですが、実際にプログラムを作ってみようとすると意外と複雑になる「加算と乗算を含む式の計算」を行うことができるものを作成します。なお、ここでは「*」は乗算を意味するとします。一見すると簡単そうですが、「1 * 2 + (3 + 4) * 5 + 6」や「1 + 2 * (3 + 4) + 5 * 6」のような式も計算できるような仮想計算機を用意してください、といわれると案外と難しいと感じるのではないでしょうか。
それでは、早速これを実現するための「スタックを使った仮想計算機」について説明をしたいところですが、まずは、スタックを使う利点を理解しておくことが大切です。そのため、「後置記法」という式の表現について先に解説をします。
では、「後置記法による式の表現」がなぜ必要なのか、について説明をしましょう。そもそもコンピュータ(電子計算機)というのは、その名のとおり計算をするための機器のことです。これを使っていかに簡単に効率よく計算をすれば良いか、ということが研究されて今日に至るわけです。
数の表現について考えてみても、人間は数の計算には10進数をよく使いますが、コンピュータでは2進数を使った計算の方が実現しやすいので、2進数が使われます。これと同じように、人間にとって分かりやすい式の表現とコンピュータにとって都合の良い式の表現は違っているのです。
計算式の記法の種類
一般的に「1と2とを足す」を意味する算術式は、「1 + 2」のように演算の対象となる値(operand、オペランド、被演算子)の間に演算子(operator、演算子)を置きます。この表現方法を中置記法(infix notation)といいます。
これに対し、後置記法(postfix notation)では、演算子はオペランドの後ろに置きます。つまり、「1 + 2」は「1 2 +」と表記されるわけです。勘の良い人は、オペランドの前に演算子を置くことを考えるかもしれません。その記法にも名前が付いていて、前置記法(prefix notation)といいます。この場合は、例の算術式は「+ 1 2」と表記できます。
| 記法 | 表記例(1と2とを足す) |
|---|---|
| 前置記法 | + 1 2 |
| 中置記法 | 1 + 2 |
| 後置記法 | 1 2 + |
| 表1 算術式の表記 | |
コラム ポーランド記法
前置記法はポーランド人の論理学者が考え出したものなので、ポーランド記法(Polish Notation)と呼ばれることもあります。一方の後置記法は、これを逆にしたものになるので、逆ポーランド記法(Reverse Polish Notation)と呼ばれることがあります。前置記法は見慣れない人が多いかもしれませんが、プログラミング言語のLispなどで採用されています。開発者なら一度は、EmacsやMeadowといったLisp搭載のエディタを使ったことがあるかと思います。これらのエディタでは、「M-x lisp-interaction-mode」(M-xはメタキーとxを同時に押下)と入力して、Lispの実行モードにできます。そこで、「(+ 1 2)」などの式を入力して、「C-j」(Ctrlキーとjを同時に押下)とすると、「3」という結果が表示されます。
これだけだと、「こんな簡単な式の変形をすることが、なぜコンピュータにとってうれしいのか?」と、疑問に思うことでしょう。答えは、後置記法の次の2つの特徴に注目すると分かってきます。
- かっこによる演算子の優先度指示が必要ない
- オペランドが先に現れ、左から順に文字を読んで計算ができる
後者については、スタックを使って計算をするときに関係してきますので、そのときに説明します。ここでは、「かっこによる演算子の優先度指示が必要ない」という点について簡単な具体例を見ながら確認をしてみましょう。
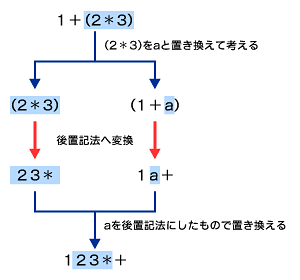
例1 「1 + 2 * 3」を後置記法にする
例えば、「1 + 2 * 3」という算術式があったとすると、後置記法ではどのように表記することになるでしょうか? ただし、「*」は乗算を表すとします。この算術式では、乗算は加算よりも優先度が高いので、「1 + (2 * 3)」という算術式のかっこを省略しているといえます。「(2 * 3)」を「a」と置き換えてみると、「1 + a」になりますから、この部分は「1 a +」と表記することになります。さらに、aの中を後置記法で記述すると「2 3 *」になります。これらを考え合わせると、後置記法では、「1 2 3 * +」と表記するのが答えになります。後置記法では、かっこを付ける必要はないのですが、あえてかっこを付けるとしたら、「(1 (2 3 *) +)」と表記することになります。
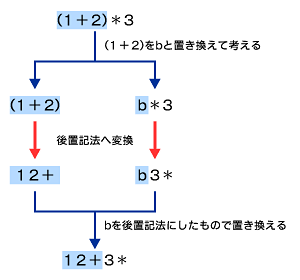
例2 「(1 + 2) * 3」を後置記法にする
それでは次に、「(1 + 2) * 3」はどうなるかを考えてみましょう。先ほどと同様にして、「1 + 2」を「b」と置き換えてみると、「b 3 *」となります。次に、bの中を後置記法で記述すると「1 2 + 3 *」となります。こちらもあえてかっこを付けるとしたら、「((1 2 +) 3 *)」となります。
ほかにも、「1 + 2 * (3 + 4)」や「(1 + 2) * (3 + 4)」についても同じように答えを出せます。それぞれ、「1 2 3 4 + * +」「1 2 + 3 4 + *」となります。
慣れないとすぐには分からないかもしれませんが、左から1文字ずつ見ていき、演算子が出てきたら直前の2つの値がオペランドであると見ればいいだけなので、かっこを付けなくても、どのような計算をするのかが決まります。確認してみましょう。
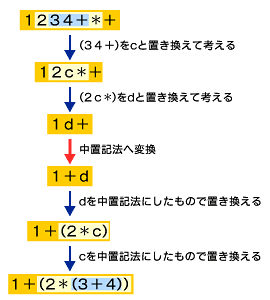
例3 「1 2 3 4 + * +」を中置記法にする
「1 2 3 4 + * +」は、左から1文字ずつ見ていくと、+演算子が最初の演算子となります。この演算子を見た時点で、「3 4 +」(「c」とします)が「3 + 4」を意味する1つの式であることが分かります。次に*演算子が出てくるので、「2 c *」(「d」とします)が「2 * (3 + 4)」を意味する1つの式であることが分かります。最後に、+演算子を見て、全体で「1 d +」という計算を表していると分かるので、中置記法では「1 + (2 * (3 + 4))」であることを復元できます。演算子の優先度を考慮すると、省略可能なかっこがあるので、「1 + 2 * (3 + 4)」だということになります。
例4 「1 2 + 3 4 + *」を中置記法にする
もう1つだけ確認をしておきます。「1 2 + 3 4 + *」についても、左から順に1文字ずつ見ていき、+演算子が出てきたところで「1 2 +」(これを「e」とします)が「1 + 2」を意味する1つの式であり、次に+演算子が出てきたところで「3 4 +」(これを「f」とします)が「3 + 4」を意味する1つの式であることが分かります。さらに、*演算子が出てきたところで、「e f *」という計算をしていることが分かるので、全体としては中置記法では、「(1 + 2) * (3 + 4)」という算術式を復元できます。
まとめ
このように、中置記法では必要だったかっこを、後置記法では使う必要がありません。この利点をよく理解しておきましょう。ここまでくれば、「1 * 2 + (3 + 4) * 5 + 6」や「1 + 2 * (3 + 4) + 5 * 6」のような式を計算できるような仮想計算機を作成するために後置記法がどれだけ重要なのか、分かってきたのではないでしょうか。
最初にこれらの式を見たときに、これらを計算するためには、かっこを何らかの方法で処理する必要があると思ったはずです。後置記法で式を表現することにすれば、その必要がなくなるのです。
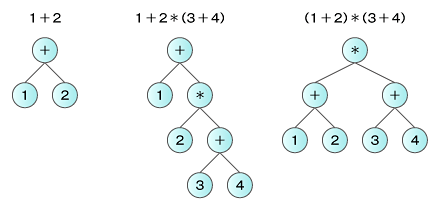
コラム 算術式と木構造
算術式を木構造を使って表現する方法もあります。オペランドを葉として、節に演算子を置きます。例として、「1 + 2」「1 + 2 * (3 + 4)」「(1 + 2) * (3 + 4)」を木構造で表現する図4を添付しておきます。式の構造が一目で分かるのではないでしょうか。
Copyright © ITmedia, Inc. All Rights Reserved.