前回までの解説でコンパイラが生成するオブジェクトコードとそれを実行する仮想マシンについては理解できたはずです。コンパイラが出力するものについては明確にできましたから、次はコンパイラへ入力するソースコードについて考えることにします。
ソースコードには、プログラムを記述することになりますから、それをどのように記述するかを自分で決める必要があります。つまり、プログラム言語の文法を自分で定義するのです。今回はこの方法について解説をします。
コンパイラの仕様(どのように動くか? を決める)
本連載でターゲットとしている仮想マシンは非常に単純なものですから、バイナリファイルを毎回手作業で作成することも可能です。
とはいえ、簡単な計算をするために毎回この作業をするのは大変ですから、普段使い慣れている数式を使って計算できるようにしたいところです。そのためには、数式を入力したテキストファイルをソースコードと見なし、それから仮想マシン用オブジェクトコード(バイナリファイル)を生成するコンパイラを作成すればよいということになります。
コンパイラのプログラムを作成するということになると、仕様を考える必要があります。コマンドラインで実行するツールとして開発することにして、起動クラス「Svm1c」を用意します。入力は、Svm1用プログラミング言語で記述されたソースコードとします。出力結果としては、仮想マシン「Svm1」用のオブジェクトコードとしたいので、起動時の引数でSvm1用プログラミング言語で記述されたソースコードのファイル名を指定することにします。結果のオブジェクトコードは「a.svm」というファイルに保存することにします。
| 実行方法 | java Svm1c <ファイル名> |
|---|---|
| 実行結果 | コンソールにコンパイル成功/失敗を表示。成功時は「a.svm」ファイルを生成 |
| 入力 | Svm1用プログラミング言語ソースコードファイル |
| 出力 | 入力に応じた仮想マシン「Svm1」用のオブジェクトコード「a.svm」 |
| 表1 コンパイラ「Svm1c」の仕様 | |
コンパイラの仕様を上記のように簡単に書きました。出力結果については、これまでの連載の内容を理解していれば十分分かるはずですが、入力についてはよく分からないはずです。それは、この仕様に「Svm1用プログラミング言語」というものが突然出てきているからです。
読者の皆さんは「初めて聞くプログラミング言語だ」と思ったはずですが、それは当然のことです。なぜなら、Svm1用プログラミング言語は、これから定義するプログラミング言語だからです。コンパイラの基礎を理解するに当たり、既存のプログラミング言語を使用することもできるのですが、複雑過ぎるために基本中の基本を理解するのに十分な言語を定義することにしました。
「正しい式」と「正しくない式」の判定
ということで、Svm1用プログラミング言語(以降、「S1s」とします)の定義が必要になります。言語の定義をするということは、その言語の文法を決めるということになります。文法が決まっていると、ある文に対して、それが「正しい文」か「正しくない文」か、ということを判定できるようになります。コンパイラを作成するには、この判定をコンピュータができるように、言語を設計したりプログラムを作成したりする必要があります。
抽象的な話をしても分かりにくいと思うので、簡単な例を見ながら考えてみましょう。ここでは、数式を言語と見なしてみることにします。「数式が何で言語なのか」と疑問に思うかもしれませんが、正しい順番で文字が並んでいないと正しい数式にならないことを考えてもらうと、何らかの規則に基づいて数式も書く必要があると分かるはずです。そういう視点から、ちょっと強引な気もするかもしれませんが、言語と見なすことができるのです。
数式では文ではなく式が単位となりますから、「正しい式」と「正しくない式」の判定について見てみます。「1+2」「1+2-3」「1*(2+3)」といった式は「正しい式」ですが、「1+2-」「1r2-3」「1*2+3)」といった式は「正しくない式」です。「1+2-」は「-」の右項がありませんし、「1r2-3」の1と2の間のrは何を意味するのか分かりませんし、「1*2+3)」では括弧の対応が取れていません。
この判定ができるのは、暗黙のうちに数式で使われている数字や演算子記号などがどのような順番で記述されるのかを知っているからですが、コンピュータには機械的な手順で判定する方法が必要です。どうすればよいのでしょうか。
| 正しい式 | 「1+2」「1+2-3」「1*(2+3)」 |
|---|---|
| 正しくない式 | 「1+2-」「1r2-3」「1*2+3)」 |
| 表2 正しい式と正しくない式 | |
BNF(バッカス記法)って何だ?
コンピュータと相性の良い表現方法の1つとして、BNF(Backus-Naur Form、Backus Normal Form)という記法があります。これを使って、数式を表現し判定する方法を紹介します。BNFは日本語ではバッカス記法と呼ばれています。コンピュータとの相性の良さについて厳密に解説するのは難しいので、ここでは分かりやすさを優先して判定方法の手順を説明します。あらかじめご了承ください。それでは、早速BNFについて見てみましょう。
「1けたの2進整数」をBNFで表すと
このBNFを使うと、例えば、1けたの2進整数は次のように表現できます。ここでは、1けたの2進整数を<one-figure binary digit>と表現しています。
<one-figure binary digit> ::= 0|1
この例では、「0か1のどちらか」という意味になります。「生成」という意味がよく分からないかもしれませんが、取りあえず、この1行で「1けたの2進整数は0か1のどちらかである」ということが定義されていますので、その点を理解できれば十分です。
コラム 「BNFの記号の名称」
なお、「左辺::=右辺」は生成規則(production rule)と呼ばれます。また、
ここで話を戻すと、「式が正しいか正しくないかを判定する方法」としてBNFを紹介しましたが、ピンと来ない人が多いと思います。そこで、この例で「ある文字列が、1けたの2進整数か否か」を判定してみましょう。といっても、この例では規則が非常に単純なので、判定はとても簡単にできてしまいます。
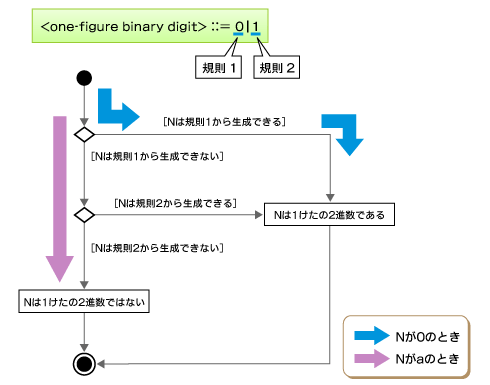
例1:「0」という文字列が「1けたの2進整数」であるかの判定
例えば、「0」は「1けたの2進整数」です。なぜなら、「
例2:「a」という文字列が「1けたの2進整数」であるかの判定
ほかの例として、「a」について判定してみましょう。これは「1けたの2進整数」ではありません。なぜなら、「a」は「<one-figure binary digit> ::= 0|1」の右辺の選択肢に含まれていないからです。当たり前のように感じると思いますが、この点を理解しておくことが重要です。例1、例2の判定フローを描くと、次のようになります。
「1けたの10進整数」をBNFで表すと
BNFについて理解を深めるために、もう少し例を見てみましょう。例えば、「1けたの10進整数」は次のように表現できます。
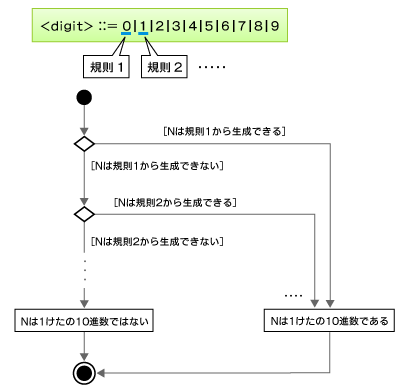
<digit> ::= 0|1|2|3|4|5|6|7|8|9
ここでは「1けたの10進整数」を<digit>という非終端記号で表現しています。この例でも、ある文字列が「1けたの10進整数」かどうかを判定するのは簡単です。
Copyright © ITmedia, Inc. All Rights Reserved.