Rで実践する統計的検定の初歩:実践! Rで学ぶ統計解析の基礎(2)(1/3 ページ)
オープンソースの統計処理言語・環境の「R」を使って実践的な統計解析を身に付けよう。連載2回目の今回は、統計的検定とは何かというざっくりした説明を軸に、やはりRで実際に計算をしてみます。
前回のおさらい
今回も統計処理言語の「R」を使って、いくつか具体的なデータから計算をしてみたいと思います。そもそも統計的検定とは何か、どういうことをやっているのかという概説と、統計的検定に対する批判についてもご紹介したいと思います。
まずは前回のおさらいです。
前回の終わりのほうで帰無仮説(きむかせつ)である「Jリーガーの月別出生数分布は日本人の月別出生数分布と同じである」かどうかを統計学的に検査するために、カイ二乗検定を導入しました。
まずは前回の結果を再現することから始めましょう。必要なデータを読み込んで、変数を設定します。もしもすでに以下のコードを走らせている場合は、同じことを2度する必要はありません。
> conn <- url("http://euler.bakfoo.com/public/jleagers.rda")
> load(conn)
> conn <- url("http://euler.bakfoo.com/public/japanpop.rda")
> load(conn)
> slice <- 7:10
> japrecent <- apply(data.japan[slice,], 2, sum)[-c(1,2)]/length(slice)
> ls()
[1] "conn" "data.japan" "data.jleagers" "japrecent"
[5] "slice"
data.jleagersにはJリーガーの月別出生数分布が入っていて、data.japanには日本人の月別出生数分布が入っています。japrecentには1975年から1990年までの日本人の月別の出生数が入っています。そして、Rにおいて、カイ二乗検定を実行する手順は次のとおりでした。
> prob <- japrecent/sum(japrecent) > chisq.test(data.jleagers,p=prob) Chi-squared test for given probabilities data: data.jleagers X-squared = 89.5635, df = 11, p-value = 2.03e-14
この結果、p-valueが十分に小さいということで、帰無仮説である「Jリーガーの月別出生数分布は日本人の月別出生数分布と同じである」という言明は採用できない(正確には採用しづらい)、棄却できるということでした。この一連の検定は、カイ二乗適合度検定と呼ばれます。標本データの分布(この場合Jリーガーの月別出生数分布)が、それが所属する集団の分布(この場合、日本人の月別出生数分布)と同じであるかどうかを検査する方法です。
ここで当然次のような疑問が沸いてくると思います。なぜ帰無仮説を調べるのか? カイ二乗というのは何か? p-valueはどういう計算により導きだされたのか?そして、このカイ二乗検定を含んだ統計的検定は完全無欠のツールなのか?
この一連の計算についての原理をここで説明します。
カイ二乗検定の原理
次の数学定理が成り立っていることが、カイ二乗適合度検定が成立する根拠になっています。
定理
カテゴリ数がk、あるカテゴリiに該当する観測度数をniそのカテゴリの期待度数をeiとするときに、以下の確率変数x2
の分布が、サンプル数を十分に大きくしたときに自由度k-1のカイ二乗分布に近づく。
いきなり数式を出してしまいましたが心配しないでください。この後すぐに意味を解説します。
ここで「カテゴリ」とは、サンプルをとるときの区分けのことです。例えばいままで話題にしてきたJリーガーの月別出生数の場合、data.jleagersにある、jan,、feb、mar……、という誕生月に区分けをして出生数を数えますので、誕生月がカテゴリになります。
> data.jleagers
jan feb mar apr may jun jul aug sep oct nov dec
[1,] 58 52 60 125 137 110 101 98 108 88 67 69
この小文では、上記の定理の証明にまで立ち入りません。興味がある読者は、手頃な数理統計学の教科書をあたってください。筆者がよく利用するのは、学生時代からお世話になっている以下の本です。
- P.G. ホエール「入門数理統計学」培風館 p225
証明はしない代わりに、定理の意味を簡潔に説明したいと思います。
まず、定理にあるx2とは、カテゴリiごとの観測度数と期待度数の差の相対値、
を、すべてのカテゴリについて足し合わせたものです。つまり、このx2値は観測した分布が、期待している分布に比べてどれだけ類似しているかを表す値です。
このために、x2が、自由度k-1のカイ二乗分布を仮定したときに、カイ二乗分布の確率として十分に小さな値をとるか、つまり観測した分布と期待している分布がどの程度の確率で同じであるかどうか、ということが検査の基準になります。
そもそも確率変数、確率密度関数とは
ここでカイ二乗分布とは、ある確率密度関数を持つ連続確率分布のことです。これまで確率変数の説明も正規分布の説明も確率密度関数の説明もしていないので、いきなり何のこっちゃというカンジになるのではないかと思います。そこで簡単に説明しますと、確率や統計の世界では、あらゆる変数が確定的な値を持つわけでなく、ある確率の「幅」を持つのです。これを確率変数といいます。
例えば高速道路を100km/hで運転するとします。そのときにドライバーはできるだけ100km/hを保とうとしても、実際には路面状況や他の自動車との関係、そして風やトンネルなどの外部要因によって、100km/hを中心に、ある幅をもった値になるはずです。
この高速道路を走る車の速度のように、「幅」をもった変数が確率変数で、その確率変数が持つ幅の形を確率密度関数といいます。確率密度関数は「密度」という言葉のとおり、積分すると全確率、つまり「確率=1」になるような関数です。
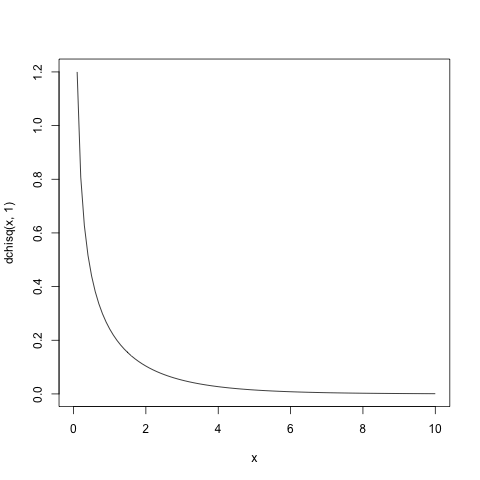
定理にあるx2という確率変数が持つ、カイ二乗分布の確率密度関数とは、自由度をパラメータとして、以下のような形をしたものです。
この図を書くには、Rにある組込みのカイ二乗確率密度関数dchisqを初等関数描画関数curveと組みわせて、次にのようにします。
> curve(dchisq(x,1), from=0, to=10)
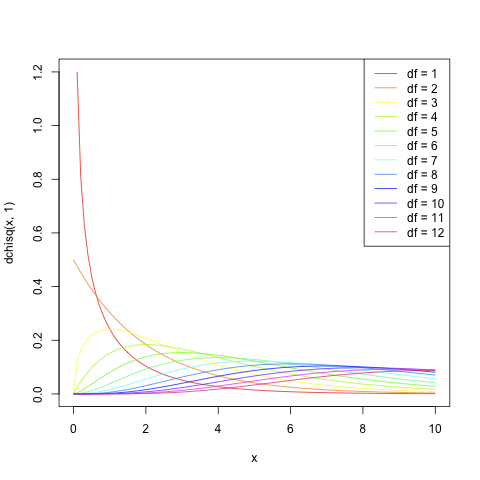
ちなみに、カイ二乗確率密度関数の自由度を1から12まで動かすと次のようになります。
Copyright © ITmedia, Inc. All Rights Reserved.