第1回 TensorFlowとは？ 入門連載始動！ データフローグラフ、事例、学び方：TensorFlow入門（2/3 ページ）

TensorFlowの概要と適用範囲を説明。最重要な基本概念であるデータフローグラフについて解説する。また、深層学習との関係や、事例、学び方についても紹介する。

[安部晃生，DATUM STUDIO]

TensorFlowと深層学習

TensorFlowとニューラルネットワーク

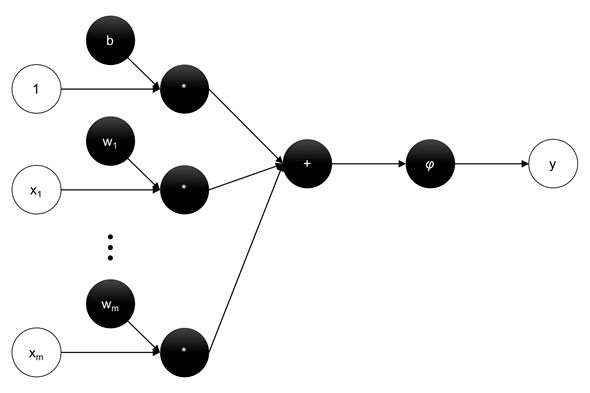
　ニューラルネットワークを簡単に概観しておこう。ニューラルネットワークはもともと神経細胞（ニューロン）における情報伝達の仕組みを数理化したモデルで、以下のように表される人工ニューロンを組み合わせることでネットワークを構築したものである。

　ここでyは出力、 ϕは活性化関数（activation function）、 w_iは重み（weights）、 x_iは入力、bはバイアス項（bias term）であり、 W=(b, w₁, ⋯ , w_m)^⊤、 x=(1, x₁, ⋯ , x_m)^⊤とした。また、演算 ⋅はドット積（要素同士の積の和）を表す。この人工ニューロンをデータフローグラフで表現すると、以下のようになる。

図3　人工ニューロン
入出力を白丸、パラメーターおよび演算を黒丸で表している。

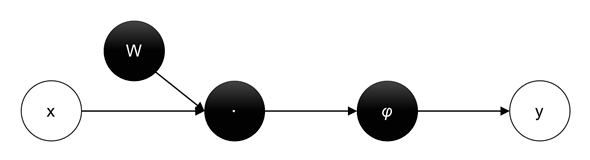
　図3を単純化して表現すると、図4のようになる。

図4　単純化した人工ニューロン
図3と同様に入出力を白丸、パラメーターおよび演算を黒丸で表している。

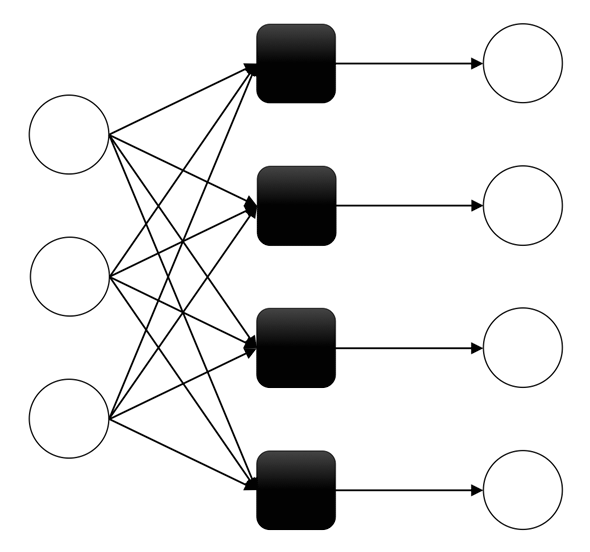
　図4をさらに単純化して、演算部分の黒丸を黒四角として、複数の入出力をつなげてネットワーク状にしたものがニューラルネットワーク（Neural Network）である（図5）。

図5　ニューラルネットワーク
黒四角は人工ニューロンにおける演算を表す。

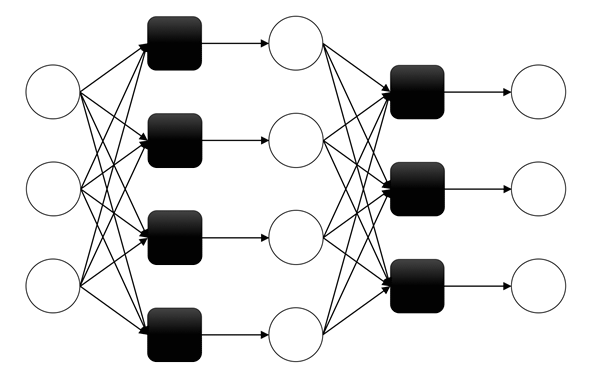
　そのニューラルネットワークの層を重ねて層を深くすることで構築したニューラルネットワークがディープニューラルネットワーク（Deep Neural Network）である（図6）。

図6　ディープニューラルネットワーク
黒四角は人工ニューロンにおける演算を表す。人工ニューロンの出力を次の層の入力として用いることで、ニューラルネットワークを多層化している。

　入力層（input layer）と出力層（output layer）の間にある中間層（Intermediate layer）は、ユーザーからはその入出力状態が見えないため、隠れ層と呼ぶ。通常、ニューラルネットワークがディープであるとは、隠れ層が2層以上ある状態を指す。なお、図6のように、前の層のすべての出力が、次の層のすべての人工ニューロンの入力に利用されている状態を全結合（fully connected）という。

　人工ニューロンは単純なデータフローグラフであり、（ディープ）ニューラルネットワークは人工ニューロンを組み合わせたものであるから、ニューラルネットワークは結局、データフローグラフで表現される単純な演算処理であり、TensorFlowの得意とする演算処理であることが分かる。

機械学習とニューラルネットワーク

　深層学習とは、主にディープニューラルネットワークを用いた機械学習の枠組みである。

　機械学習は、人間が行っている学習の仕組みをコンピュータープログラムに落とし込んだものだ。その手法はさまざまあり、ディープラーニングはその一分野にすぎない。過去のデータを基に学習を行い、新しいデータに対して予測を行ったり、新しい何かを生成したり、あるいは与えられたデータそのものから何らかの示唆を得られたりするような、モデル（model）を作成する。

　モデルとは、データを入力して何らかの出力を行う数学的な関数のようなものだと思ってもらえばよい。深層学習においては、ニューラルネットワークにおける各人工ニューロンのパラメーター（W）を設定することで、入力に対してディープニューラルネットワークの演算処理を行い、出力を得ることができるようになる。このときのパラメーターが定められたニューラルネットワークのことを「モデル」と呼び、パラメーターを求めることを「学習」と呼ぶ。

　入力に対する出力の精度を高めるためには、適切にパラメーターを設定する必要がある。「精度が高い」という定義はさまざま考えられるが、通常は損失関数（loss function）と呼ばれる関数で評価する。詳細は本稿では割愛するが、適切なネットワークと損失関数の定義を行うことで、ディープニューラルネットワークのパラメーターの最適化を実行できる。最適化を行う手法もさまざまあるが、よく知られた最適化手法（optimizer）や損失関数については、あらかじめTensorFlowに定義されているため、特別な理由がなければライブラリ中から選択すればよい。具体例は本連載の第5回と第7回を参考にしてほしい。

なぜTensorFlowで深層学習を行うのか？

　TensorFlowは、データフローグラフによりディープニューラルネットワークを構築できる。データフローグラフによって構築されたディープニューラルネットワークのパラメーターは、TensorFlowによって定義された手法により、最適化できる。つまり、TensorFlowは汎用化された数値計算ライブラリではあるものの、TensorFlowは深層学習を行うために十分使いやすい手法を実装しており、深層学習の利用に適したライブラリであるといえる（最初に引用したように、もともとニューラルネットワークの研究のために作られたものなので当然なのだが）。