[Python入門]集合:Python入門(2/4 ページ)
Pythonでは「集合」も標準でサポートされている。その基本と、集合の比較や和/差/積/対称差の求め方、変更不可能な集合などについて見ていこう。
要素の追加:addメソッド
集合に要素を追加するには、addメソッドを使用する。
addメソッド
add(item)
集合にitemを要素として追加する。
| パラメーター | 説明 |
|---|---|
| item | 集合に追加する値。itemに指定したものが、その集合の要素となる。つまり、itemに集合を渡した場合は、その集合そのものが要素として追加される |
| addメソッドのパラメーター | |
以下にaddメソッドの使用例を示す。
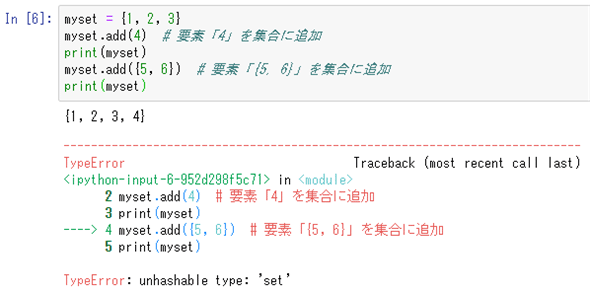
myset = {1, 2, 3}
myset.add(4) # 要素「4」を集合に追加
print(myset)
myset.add({5, 6}) # 要素「{5, 6}」を集合に追加
print(myset)
実行結果は次のようになる。
2つ目の呼び出しでは「{5, 6}」という集合をaddメソッドに渡しているが、これにより「5」と「6」という要素が追加されるのではなく、エラー(TypeError例外)が発生している点に注意しよう。集合を集合の要素とすることはできない。リストも同様だ。これは集合やリストは変更可能なオブジェクトだからだ。後から要素を変更できるものを集合の要素にしてしまうと、集合内で要素の一意性が保たれる保証ができない、つまり後から要素が重複する可能性がある(エラーメッセージにある「ハッシュ化できない型」というのは、そうした意味合いである)。
要素の削除:removeメソッド/discardメソッド/popメソッド
集合から要素を削除するには、removeメソッドあるいはdiscardメソッドを使用する。
removeメソッド/discardメソッド
remove(item)
discard(item)
removeメソッドとdiscardメソッドは、共に指定されたitemを集合から削除する。集合に指定されたitemが存在しない場合に、removeメソッドはエラー(KeyError例外)を発生するが、discardメソッドは集合に指定されたitemが存在しなくてもエラーを発生しない。
| パラメーター | 説明 |
|---|---|
| item | 集合から削除したい値 |
| removeメソッド/discardメソッドのパラメーター | |
2つのメソッドの違いは、引数に指定した値が集合に存在しなかったときに、エラー(KeyError例外)を発生するかしないかだ。以下に使用例を示す。
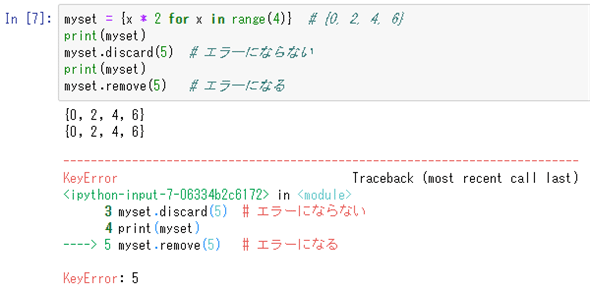
myset = {x * 2 for x in range(4)} # {0, 2, 4, 6}
print(myset)
myset.discard(5) # エラーにならない
print(myset)
myset.remove(5) # エラーになる
実行結果を以下に示す。
集合内での要素の有無を気にすることなく、要素の削除を行いたければdiscardメソッドを、要素がないときには何か別の処理を行う必要があればremoveメソッドを呼び出す。あるいはin演算子を使って要素の存在確認を行った上でremoveメソッドを呼び出すことも考えられる。
myset = {x * 2 for x in range(4)} # {0, 2, 4, 6}
if 5 in myset:
myset.remove(5)
この他にもpopメソッドによる要素の取得と削除を行える。これは集合に含まれているいずれかの要素を削除して、それを戻り値とする。以下に例を示す。
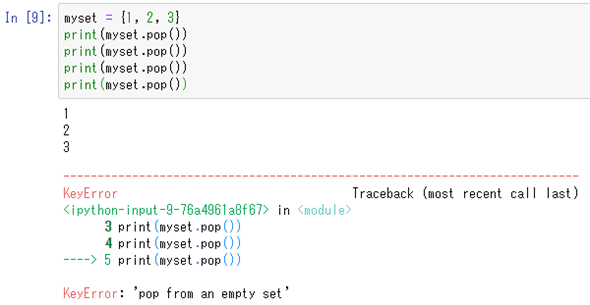
myset = {1, 2, 3}
print(myset.pop())
print(myset.pop())
print(myset.pop())
print(myset.pop())
以下に実行例を示す。ただし、どの要素が削除されるかは任意だ。また、空の集合に対してpopメソッドを呼び出すとエラー(KeyError例外)が発生する。
集合の操作
集合でも、リストやタプル、辞書と同様に、要素数の取得、要素の存在確認などの操作が可能だ。これらについてまず簡単にまとめておこう。なお、以下の表では変数mysetに集合「{1, 2, 3}」が代入されているものとする。
| 操作 | 方法 | 例 |
|---|---|---|
| 要素数を求める | len(集合) | len(myset)→3 |
| 最大の要素を求める | max(集合) | max(myset)→3 全ての要素が比較可能な場合。集合に文字列と数値が含まれている場合などはエラー(TypeError例外)となる |
| 最小の要素を求める | min(集合) | min(myset)→1 全ての要素が比較可能な場合。集合に文字列と数値が含まれている場合などはエラー(TypeError例外)となる |
| 集合に特定の要素が含まれているかどうかの確認 | 要素 in 集合 | 100 in myset→False |
| 集合に特定の要素が含まれていないかどうかの確認 | 要素 not in 集合 | 100 not in myset→True |
| 集合をコピーする | 集合.copy() | myset.copy()→{1, 2, 3} 集合の浅いコピーが戻り値となる |
| 集合の全要素を削除する | 集合.clear() | myset.clear() |
| 集合の要素を並べ替える | sorted(集合) | sorted({3, 2, 1})→[1, 2, 3] 集合にはsortメソッドがないが、組み込みのsorted関数を使って要素を並べ替えられる。戻り値はリストになる点に注意 |
| 集合の操作 | ||
集合の比較
集合が複数あるときには、それらを比較できる。集合Aが集合Bに含まれているかどうか(部分集合)、集合Aと集合Bが等しいかどうか、集合Aと集合Bには共通する要素がないかどうかなどだ。
集合が等しいか等しくないかを調べる
2つの集合が等しい(2つの集合が全く同じ要素を持っている)かどうかは==演算子で調べられる。同様に、2つの集合が等しくない(2つの集合の要素が完全には一致しない)かどうかは!=演算子で調べられる。以下に例を示す。
myset1 = {1, 2, 3}
myset2 = {3, 2, 1}
myset3 = {1, 2, 3, 4}
print(myset1 == myset2)
print(myset2 == myset3)
print(myset1 != myset3)
実行結果を以下に示す。
集合myset2は「{3, 2, 1}」という要素を持ち、集合myset3は「{1, 2, 3, 4}」という要素を持っている。そのため、両者は異なる集合と判定されている。だが、これらの集合の間には包含関係がある。これを調べる方法を次に見てみよう。
部分集合/上位集合であるか(包含関係)を調べる:issubsetメソッド/issupersetメソッド
集合Aと集合Bがあったときに、集合Aの全要素を集合Bも持っているとすると、集合Aは集合Bの「部分集合」、集合Bは集合Aの「上位集合」と呼ぶ。集合Aにはない要素を集合Bが持っていれば、さらに集合Aは集合Bの「真部分集合」、集合Bは集合Aの「真上位集合」と呼ぶ(集合Aが持つ全要素を集合Bが持っており、集合Bが持つ全要素を集合Aが持っている、つまり2つの集合が等しい場合には、一方がもう一方の部分集合かつ上位集合ともなる)。
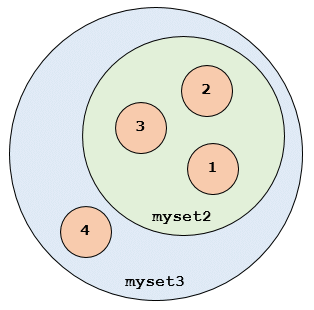
例えば、先ほどの集合myset2(myset1でも同様だ)とmyset3の関係を図にすると、次のようになる。
この場合、集合myset2は集合myset3の部分集合であり(この場合は真部分集合)、集合myset3は集合myset2の上位集合である(同じく、この場合は真上位集合)。
ある集合が別の集合の部分集合であるかどうかは、以下に示す3つのメソッドと演算子で調べられる。
- issubsetメソッド
- <=演算子
- <演算子
issubsetメソッドと<=演算子は「ある集合が別の集合の部分集合であるかどうか」を調べるもので、<演算子は「ある集合が別の集合の真部分集合であるかどうか」を調べるものだ。
同様に、ある集合が別の集合の上位集合であるかどうかは、以下に示す3つのメソッドと演算子で調べられる。
- issupersetメソッド
- >=演算子
- >演算子
issupersetメソッドと>=演算子は「ある集合が別の集合の上位集合であるかどうか」を調べるもので、>演算子は「ある集合が別の集合の真上位集合であるかどうか」を調べるものだ。
issubsetメソッドとissupersetメソッドの構文を以下に示す。
issubsetメソッド/issupersetメソッド
issubset(other)
issuperset(other)
集合がもう一つの集合otherの部分集合かどうか(issubsetメソッド)、あるいは上位集合かどうか(issupersetメソッド)を調べる。otherには集合だけではなく、任意の反復可能オブジェクトを指定可能。
| パラメーター | 説明 |
|---|---|
| other | 比較対象の集合もしくは反復可能オブジェクト |
| issubsetメソッド/issupersetメソッドのパラメーター | |
残る4つの演算子は2つの集合を被演算子として、包含関係を調べる。
| 演算子 | 演算結果 | 例 |
|---|---|---|
| 集合1 <= 集合2 | 集合1が集合2の部分集合ならTrue、そうでなければFalse | {0, 1, 2} <= {0, 1, 2, 3}→True |
| 集合1 < 集合2 | 集合1が集合2の真部分集合ならTrue、そうでなければFalse | {0, 1, 2} < {0, 1, 2}→False 集合1は集合2と等しいので真部分集合ではない |
| 集合1 >= 集合2 | 集合1が集合2の上位集合ならTrue、そうでなければFalse | {0, 1, 2} >= {0, 1, 2, 3}→False |
| 集合1 > 集合2 | 集合1が集合2の真上位集合ならTrue、そうでなければFalse | {0, 1, 2, 3} > {0, 1, 2}→True |
| 集合の包含関係を調べる演算子 | ||
注意しておきたいことが幾つかある。
- 上記のメソッドは集合だけではなく反復可能オブジェクトを比較対象として指定できる
- 上記のメソッドは「部分集合」もしくは「上位集合」であるかどうかを調べるもので、「真部分集合」や「真上位集合」であるかどうかは調べられない(真部分集合および真上位集合であるかどうかを調べるには演算子を使う必要がある)
- 上記の演算子の演算子は2つとも集合である必要がある
これらのメソッド/演算子の使用例を以下に示す。
myset1 = set(range(5)) # {0, 1, 2, 3, 4}
myset2 = set(range(4)) # {0, 1, 2, 3}
myset3 = set(range(4)) # {0, 1, 2, 3}
print('myset1', myset1)
print('myset2', myset2)
print('myset3', myset3)
print('myset1.issubset(myset2)', myset1.issubset(myset2)) # False
print('myset2.issubset(myset1)', myset2.issubset(myset1)) # True
print('myset1.issuperset([0, 1, 2])', myset1.issuperset([0, 1, 2])) # True
print('myset1 <= myset2', myset1 <= myset2) # False
print('myset2 >= myset1', myset2 >= myset1) # False
print('myset1 > myset2', myset1 > myset2) # True
print('myset2 < myset1', myset2 < myset1) # True
print('myset2 > myset3', myset2 > myset3) # False
print('myset2 < myset3', myset2 < myset3) # False
実行結果を以下に示す。
次に、複数の集合からその和/差/積/対称差を求める操作について見てみよう。
Copyright© Digital Advantage Corp. All Rights Reserved.