プログラムを関数にまとめて、実行結果をグラフにプロットしよう:作って試そう! ディープラーニング工作室(2/2 ページ)
ニューラルネットワークを使って学習や評価を行うコードを関数にまとめてみます。また、データセットを学習に使うものと精度評価に使うものに分割する方法、学習結果のグラフ化、過学習の抑制などについても簡単に見てみましょう。
学習と精度評価の実行
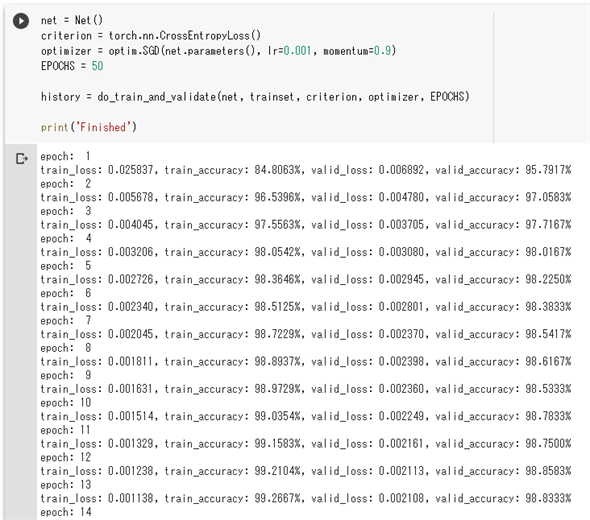
既に述べたように、学習と精度評価を実行するにはdo_train_and_validate関数を呼び出すだけです。ただし、その前にNetクラスのインスタンスや損失関数、最適化アルゴリズムの選択などを行う必要があります。また、ここでは繰り返し回数(エポック数)は50とします。
net = Net()
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
EPOCHS = 50
history = do_train_and_validate(net, trainset, criterion, optimizer, EPOCHS)
print('Finished')
このコードを実行すると、次のようにエポックごとに学習で得られた平均損失/平均正解率、精度評価で得られた平均損失/平均正解率が画面に表示されていきます。
実行完了までにはそれなりの時間がかかる点には注意してください。
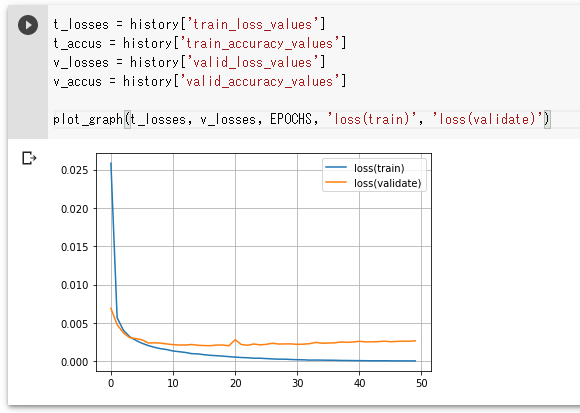
実行が終わったら、得られた損失や成果率をグラフにプロットしてみましょう。まずは、平均損失からです。以下のコードでは辞書に格納されていた各値を個別の変数に展開した後に、それらを使ってグラフをプロットしています。
t_losses = history['train_loss_values']
t_accus = history['train_accuracy_values']
v_losses = history['valid_loss_values']
v_accus = history['valid_accuracy_values']
plot_graph(t_losses, v_losses, EPOCHS, 'loss(train)', 'loss(validate)')
実行結果を以下に示します。
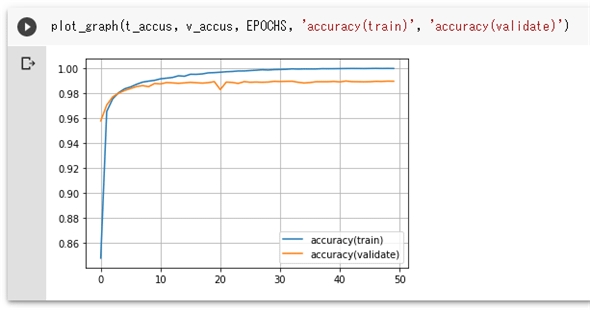
平均正解率についても同様のコードでグラフをプロットしてみます。
plot_graph(t_accus, v_accus, EPOCHS, 'accuracy(train)', 'accuracy(validate)')
実行結果を以下に示します。
これら2つのグラフを見て、学習により得られた平均損失と平均正解率と、精度評価により得られたそれらとの間に乖離(かいり)があるに気が付いたでしょうか。平均損失に注目すると、学習で得られたものは0.0000に向かって進み、最後にはほぼそうなっているのに対して、精度評価で得られた方は途中から0.0000には近づかずに一定の値(0.0025)付近でウロウロして、その後、少し増えていくようにも見えます。
この傾向はdo_train_and_validate関数呼び出しによる画面出力からも確認できます。興味のある方は実行結果を見て、学習と精度評価によって得られた平均損失と平均正解率がどんな数値になっているのか、その変化を確認してみてください。例えば、平均損失について見てみると、学習によって得られた方は0.0000へ近づこうとして、精度評価で得られた方は0.0025の辺りをうろうろしながら、しだいに大きくなっていくのが分かるはずです。
一方、平均正解率でも同様な傾向が見えます。つまり、学習で得られた方は100%へと着実に向かっているようです。対して、精度評価で得られた方では途中から99%近辺で頭打ちになっているようです。
これが意味するのは、ニューラルネットワークモデルが「過学習」の状態にあるということです(といっても、99%の精度が出ているので、それほど悪くはありません。また、未知のデータであるtestset、そのローダーであるtestloaderを使って、テストを行ってみたい方はvalidate関数にtestloaderを渡して、その結果を確認してください。その実行結果もノートブックには含めてあります)。
過学習とは
ここでいう「過学習」とは、「ニューラルネットワークが、学習に使用した訓練データに過剰に適合してしまっている状態」のことです。訓練データとは人を例にすれば、試験前に参考書で何度も解いてみる「過去問」のようなものです。そればかりを解いていると、テストで同じ問題が出たときには、「これは前にやったヤツだ」となります。それと同じように、エポックを何度も繰り返していく中で、ニューラルネットワークモデルに特定のパターンのデータが何度も入力されることで、「このときにはコレ」という解答を出しやすいように、重みやバイアスが調整されてしまっていると考えられます。
このように訓練データに過剰に適合してしまうことで、未知のデータ(過去問にはなかった問題)にはうまく対応できないかもしれません(もちろん、既に述べたようにここでは精度評価でも99%近い値が出ているので、この場合はあまり気にする必要はないかもしれません)。
過学習について詳しく見るのは別の機会として、ここでは「ドロップアウト」と呼ばれる手法を使って、これを抑制してみましょう。ドロップアウトとは、「学習の際に、ニューラルネットワークを構成するノードをランダムに無効化する」というテクニックで、これにより過学習を抑制しようというものです。
PyTorchでは、これを行うためのクラスとして、Dropoutクラスなどが提供されているので、今回はこれを全結合層に組み込んでみましょう。
実際のクラス定義を以下に示します。
class Net2(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.pool = nn.MaxPool2d(2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 16, 64)
self.dropout = nn.Dropout()
self.fc2 = nn.Linear(64, 10)
def forward(self, x):
x = self.conv1(x)
x = nn.functional.relu(x)
x = self.pool(x)
x = self.conv2(x)
x = self.pool(x)
x = x.reshape(-1, 16 * 16)
x = self.fc1(x)
x = nn.functional.relu(x)
x = self.dropout(x)
x = self.fc2(x)
return x
強調書体で表したところが変更点です。Dropoutクラスのインスタンスの生成時には、無効化するノードの割合を指定できますが、ここでは指定していません。これによりデフォルトの0.5が指定されたものと見なされ、半分のノードが毎回ランダムに無効化されるようになります。forwardメソッドでは、入力層から隠れ層へと信号が伝播するときにドロップアウトを実行するようにしてあります。
このクラスNet2を使って、上記と同様にdo_train_and_validate関数を呼び出してみましょう。
net = Net2()
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
EPOCHS = 50
history = do_train_and_validate(net, trainset, criterion, optimizer, EPOCHS)
print('Finished')
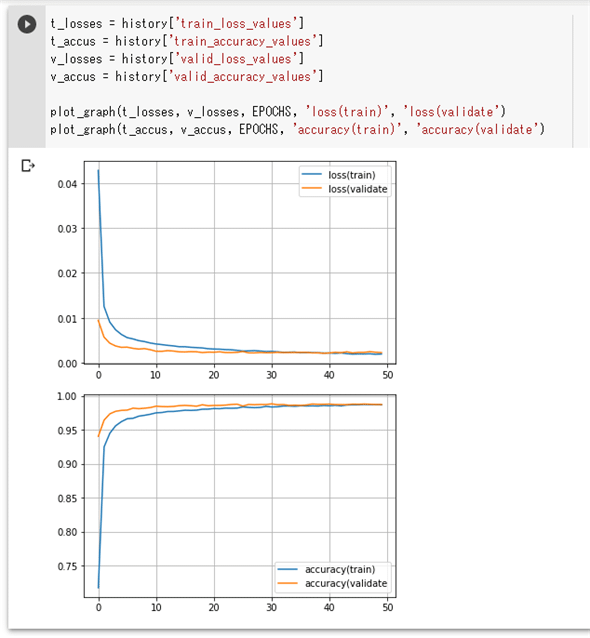
実行結果は省略して、得られた平均損失と平均正解率からグラフをプロットしてみます。
t_losses = history['train_loss_values']
t_accus = history['train_accuracy_values']
v_losses = history['valid_loss_values']
v_accus = history['valid_accuracy_values']
plot_graph(t_losses, v_losses, EPOCHS, 'loss(train)', 'loss(validate)')
plot_graph(t_accus, v_accus, EPOCHS, 'accuracy(train)', 'accuracy(validate)')
実行結果を以下に示します。
先ほどよりも、学習と精度評価における乖離が見られなくなっている点に注目してください。学習時に得られたデータと精度評価で得られたデータとで乖離が見られないというのは、両者に対して同じ程度の損失、正解率になっているということです。つまり、訓練データに対して過剰に適合していない=過学習の状態にはなっていないと見なせます。これがドロップアウトの効用です。過学習を抑制する方法としては、この他にも早期終了と呼ばれる手法などがありますが、ここでは説明は省略します。
今回はCNNによる手書き数字の認識を行うニューラルネットワークを例に、ニューラルネットワーククラスの定義だけではなく、学習や精度評価を行うコードなどを関数として構造化し、その実行結果をグラフにプロットする方法や、訓練データの分割、過学習と呼ばれる状態を抑制する方法などについて見ました。次回は、時系列データなどを扱うために使われるRNNと呼ばれるニューラルネットワークの基礎を見ていくことにします。
Copyright© Digital Advantage Corp. All Rights Reserved.