［AI・機械学習の数学］合成関数の微分（連鎖律）とニューラルネットワーク初歩の初歩：AI・機械学習の数学入門（1/2 ページ）

微分法は回帰分析だけでなく、機械学習のさまざまなタスクで使われる。特に、合成関数の微分（連鎖律）はニューラルネットワークの学習において必須となる。今回はそのための第一歩として、合成関数がどのようなものであるかを見た後、合成関数の微分法の公式とその計算方法を紹介する。

[羽山博，著]

連載目次

　微分法の基本については、その考え方や計算方法、多変数関数の偏微分など、これまでの連載で一通り見てきました。今回は、ニューラルネットワークの学習に使われる合成関数の微分（連鎖律）について、考え方と計算方法を説明します。ただし、ニューラルネットワークそのものについては、線形代数の知識も必要になってくるので、今回は詳しくは触れません。しかし、合成関数の微分ができるようになれば、ニューラルネットワークの学習を理解するにあたっての、はじめの一歩が踏み出せます。

　まずは、合成関数がどのようなものであるかというところから見ていきましょう。

目標【その1】： 合成関数を理解する

　ある関数f(x)に対して、さらに別の関数gを適用する場合、関数gは以下のように表されます。

　このg(f(x))のように、ある関数を適用した結果に別の関数を適用したものを合成関数と呼びます。なお、以下のように、関数fと関数gの合成関数をある種の演算として考え、小さな○を使って表すこともあります（この連載では○を使った書き方は使いませんが、合成関数の交換法則が成り立たないことや結合法則が成り立つことなども簡潔に表せます）。

　小さな○は、英語では「circle」や「of」などいろんな読み方がありますが、日本語では普通に「まる」と読む人が多いようです。

解説【その1】： 合成関数を理解する

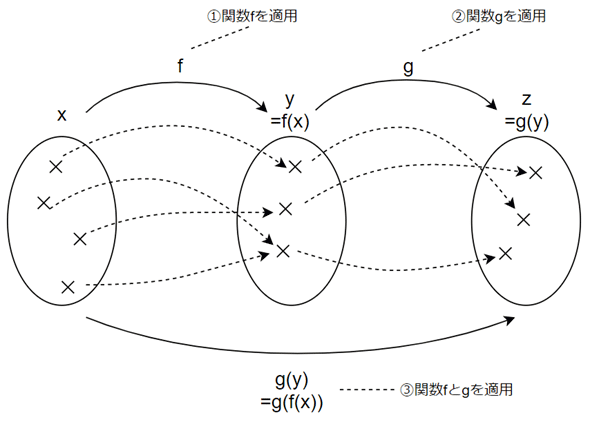
　合成関数のイメージは、以下の図を見れば一目瞭然だと思いますが、最初が肝心なので丁寧に見ていきましょう。図1は、xに対して関数fを適用し、その結果に対して関数gを適用した様子です。それを数式で書くと、

となります。

図1　合成関数のイメージ

　xの値に対して関数fを適用することはf(x)と書けますね。これをyと置きましょう。つまり、y＝f(x)です。これはすでに何度も登場している関数にすぎません。次に、そうして得られたyの値に対して関数gを適用することはg(y)と書けます。これをzと置きます。つまり、z＝g(y)です。

　ここで、g(y)にy＝f(x)を代入すると、g(f(x))になりますね（図2）。

図2　合成関数を作る

　上のようにわざわざyとかzという文字を使わなくても簡単に理解できると思いますが（むしろ回りくどいかもしれませんね）、文字で表した方が数式が簡単になることもあるので、念のため、ということで。

　では、具体的な例で合成関数の計算を幾つかやってみましょう。穴埋め問題にしておくので、考えてみてください。答えはオレンジ色の部分をクリックまたはタップすると表示されます。最初は、f(x)とかg(y)を使わずに書いてみます。

合成関数の例1

のとき、zをxで表すには、yに　2x+4　を代入して以下のようにすればいいですね。

　　z＝3y−1
　　 ＝3(　2x＋4　)−1 　　 ⋯ ［A］
　　 ＝6x＋12−1
　　 ＝6x＋11

［A］ ⋯ （2）式に（1）式を代入した

合成関数の例2

　次は、f(x)やg(y)を使って書いた別の例を見てみます。書き方が違うだけで、やるべきことは同じです。

のとき、合成関数g(f(x))を求めてみます。この場合もg(y)のyにf(x)つまり　x-1　を代入すればいいですね。

　　z＝g(y)
　　 ＝ 2(　x−1　)²＋3 　　 ⋯ ［B］
　　 ＝2(x　²　−　2　x＋1)＋3 　　 ⋯ ［C］
　　 ＝2x²−4x＋2＋3
　　 ＝2x²−4x＋5

［B］ ⋯ （4）式に（3）式を代入した
［C］ ⋯ 2乗を展開した

*1　ここでは仕組みが分かるように、x、y、zという文字を使いましたが、以下のようにxという文字だけを使って表すこともあるので、注意が必要です。

のとき、

　この場合、f(x)のxとg(x)のxは同じものではなく、単に「何らかの値を表すもの」といった意味合いで使われています。g(f(x))はg(x)のxのところにf(x)を代入したもの、と考えるといいでしょう。

　なお、g(f(x))とf(g(x))とは等しいとは限りません。上の例であればg(f(x))＝6x＋11ですが、次の計算式で示すようにf(g(x))＝6x＋2になります。

合成関数の例3

　合成関数の考え方も計算方法も簡単でしたね。複数の変数を使ったやや複雑な関数についても見ておきましょう。といっても、ここまでの計算と同様、代入と四則演算、べき乗だけしか使いません。以下のような関数があるものとします。

　ただし、a(y)はyの値によって0か1かを返す以下のような関数とします。aは定数を表すためによく使われる文字ですが、ここでは関数名として使われていることに注意してください。

　このとき、zをx₁とx₂で表すと、以下のようになります。

　　z ＝ 0.5a(y₁) ＋ 0.5a(y₂) − 0.8
　　  ＝ 0.5a( −0.5x₁ − 　0.5　x₂ ＋ 0.8 )
　　 　　　　 ＋0.5a( 0.5x₁ ＋ 0.5x₂ − 　0.2　 ) − 　0.8　 　　 ⋯ ［A］

［A］ ⋯ y₁に（5）式の−0.5x₁ − 0.5x₂ ＋ 0.8を、y₂に（6）式の0.5x₁ ＋ 0.5x₂ − 0.2を代入した

　さらに、a(z) をx₁とx₂で表すと、以下のようになります。

［B］ ⋯ zに［A］式を代入した

　念のため、合成関数がどのように適用されているかを図にしておくと、以下のようになります。

図3　合成関数が適用された様子

　ところで、（7）式などの形を見ると、aでくくって、式を簡単にできそうに見えますが、aは定数や変数ではなく関数であることに注意してください。実は、aが線形性のある関数であれば、aで「くくる」こともできるのですが、線形ではない（非線形な）関数なので以下のようにはできません*2。

［C］ ⋯ 間違った例

*2　関数の線形性というのは、aとbを定数としたとき、以下のような性質が成り立つことでしたね。

　つまり「2つの値を足してから関数を適用した値と、それぞれの値に関数を適用した結果を足した値が等しい」「定数を掛けてから関数を適用した値と関数を適用してから定数を掛けた値が等しい」という性質です（線形性については、この連載の第5回の記事を参照してください）。

簡単なニューラルネットワークの例

　実は、ニューラルネットワークの順伝播（＝入力から出力に向かう信号の流れ）は合成関数を使ってそのまま表すことができます。例えば、合成関数の例3で見た式は、XOR（エクスクルーシブ・オア）を求めるためのニューラルネットワークを表しています。XORとは、入力が等しければ0を返し、等しくなければ1を返すような論理演算のことです。つまり、表1のような計算になります。

	入力1（x1）	入力2（x2）	出力（a(z)）
	0	0	0
	0	1	1
	1	0	1
	1	1	0
表1　XORの演算

　簡単なPythonプログラムを作って、合成関数の例3の計算を実行させてみると、以下（図4）のようになります。ここでは、プログラムの内容については特に解説しませんが、ちゃんとXORの計算ができていることが分かります。

図4　XORを求めるニューラルネットワークのプログラム例（Python）

　合成関数の例3を図で表してみると図5のようになります。簡単なものですが、これを見るとニューラルネットワークそのものでであることが分かります。以下の図と式の関係は動画でも説明しているので、ぜひとも参照してみてください。

動画1　合成関数

図5　XORを求めるニューラルネットワークの図

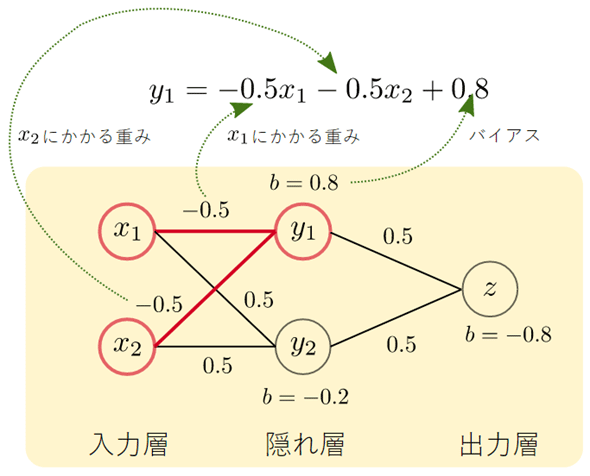
　赤い太線で示した部分が以下の式に対応しています。

［A］ ⋯ 合成関数の例3の（5）式を再掲したもの

　-0.5という値は、x₁やx₂に掛ける「重み」です。0.8という値はバイアスと呼ばれる値で、関数aを使って出力を決めるときに、0以下かそうでないかという判定ができるようにするための調整用の値です。つまり、

とする代わりに

となるように、判定の基準となる値（閾値：しきいち）を左辺に移項したものです。

　ちなみにニューラルネットワークの順伝播において、関数aのように、入力に対して出力する値を決める関数のことを活性化関数（Activation function）と呼びます。aという関数名はActivationの頭文字です。

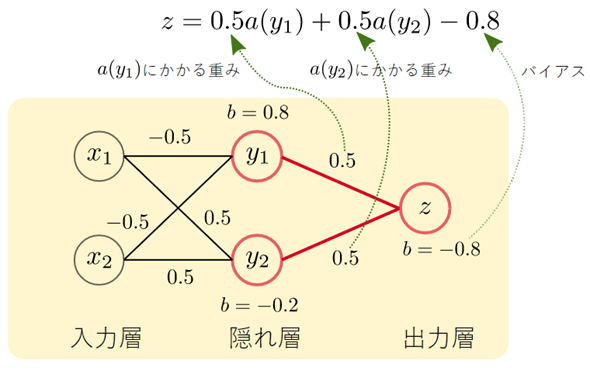
　［A］式は、y₁に入力される値を表す式ですが、y₁から出力される値は活性化関数aを適用した結果です。つまり、a(y₁)が出力され、図6の右端にあるzに入力されます。その部分と式との対応も見ておきましょう。

図6　XORを求めるニューラルネットワークの例

　やはり、図6の赤い太線で示した部分が以下の式に対応しています。

［B］ ⋯ 合成関数の例3の（7）式を再掲したもの

　［B］式は、zに入力される値を表す式です。zからの出力は、活性化関数aを適用した結果です。つまり、a(z)が結果として出力されます。x₁やx₂に0や1を入力すると、a(z)がそれらのXORを出力してくれるというわけです*3。

*3　ここでは、重みやバイアスを0.5や-0.5、-0.8などのようにあらかじめ決めていましたが、ニューラルネットワークの学習とは、それらの重みを正解の値（教師データ）を基に調整していくことに他なりません。その際、合成関数を微分（偏微分）する必要が生じてきます。しかし、ここで見た関数aは0以下の場合と0より大きい場合に分けて微分しても、微分係数は常に0にしかなりません。そこで、一般にはシグモイド関数やReLU関数と呼ばれる関数が活性化関数として使われます。

　では、次に合成関数の微分法について見ていきましょう。最初に記したように、合成関数の微分はニューラルネットワークの学習に必須です。ただし、実際にニューラルネットワークの学習に使われる式を簡潔に表すためには線形代数の知識が必要になるので、ここでは、出発点のみということで、合成関数の微分の公式とその使い方に絞って説明します。