バイアスとバリアンス(偏りと分散)のトレードオフ(Bias-Variance Tradeoff)とは?:AI・機械学習の用語辞典
用語「偏りと分散のトレードオフ」について説明。機械学習モデルによる予測において汎化誤差を最小化させるために、偏り誤差を小さくするとバラツキ(分散)誤差が大きくなり、逆にバラツキ誤差を小さくすると偏り誤差が大きくなるという、両者のトレードオフの関係性を示す。
用語解説
機械学習(や統計学)のモデルによる予測においてバイアス(偏り:Bias)とは、予測値と真の値(=正解値)とのズレ(つまり「偏り誤差:Bias error」)を指す。この予測誤差は、モデルの仮定に誤りがあることから生じる(※なお、ニューラルネットワークのニューロンおける重みとバイアスの「バイアス」とは別物なので注意)。
またバリアンス(分散:Variance)とは、予測値の広がり(つまり「ばらつき誤差:Variance error」)を指す。この予測誤差は、訓練データの揺らぎから生じる。
モデルによる予測においてバイアス(偏り誤差)が大きすぎる場合、そのモデルは入力と出力の関係性を正確に表現できていない(=訓練データでさえも正確に予測できない)といえる。いわゆる「学習不足(=過少適合:under-fitting)」の状態である。
またモデルの予測においてバリアンス(ばらつき誤差)が大きすぎる場合、そのモデルは訓練データのノイズまで学習してしまっている(=テストデータなど未知のデータでは正確に予測できない)。いわゆる「過学習(=過剰適合:over-fitting)」の状態である(図1)。
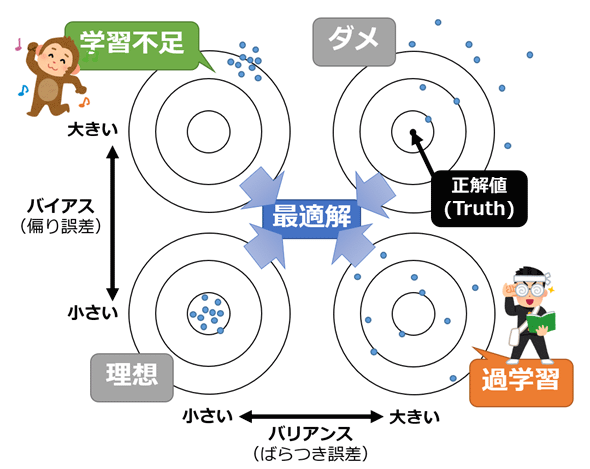
図1 バイアスとバリアンスをダーツ投げでイメージしてみよう
ダーツの中心(Bull's Eye)に向かってダーツの矢を投げるのをイメージした図。当然、全部の矢を中心(Truth:真)に当てたい(左下が理想)。しかしバイアス(偏り誤差)が大きいと左上の結果になるし、バリアンス(ばらつき誤差)が大きいと右下の結果になる。バイアスとバリアンス、両方の予測誤差に気を配りつつ、できるだけ理想に近くなるように投げる必要がある。
バイアスとバリアンスの関係は、「あちらを立てれば、こちらが立たず」というトレードオフの関係にあるため、「バイアスとバリアンスのトレードオフ(Bias-Variance Tradeoff)」と呼ばれる。この関係性は教師あり学習における根本的な問題であるため、機械学習の初心者が必ず学ぶ概念の一つとなっている。
モデルによる予測の精度(performance)を高めるには、その汎化誤差(Generalization error)を最小化する必要がある。汎化誤差は、最小化可能な誤差であるバイアスとバリアンス、さらに削除不可能な誤差(irreducible error)であるノイズの3つに分けられる(このように分けることは「バイアスとバリアンスの分解:Bias-Variance Decomposition」と呼ばれる)。
このうち、バイアスを最小化するには、訓練データからより多くを学習する必要があるが、「だから」といってバイアスを小さくし過ぎると、今度はバリアンスが大きくなってしまう。「それでは」と、逆にバリアンスを小さくしようとして小さくし過ぎると、今度はバイアスが大きくなってしまう。両者のバランスでちょうどよい最適解を探す必要があるのだ(図2)。
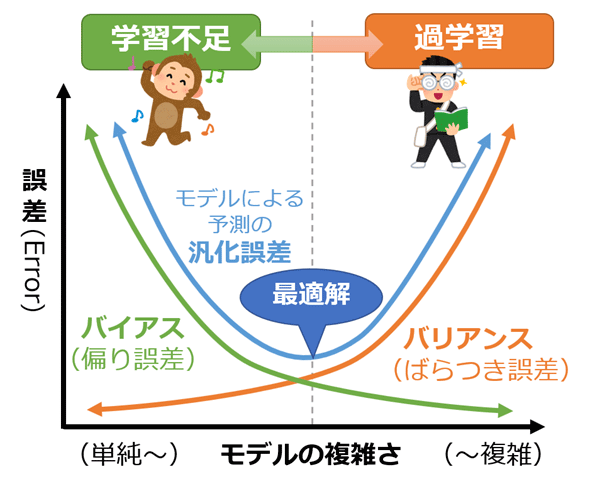
図2 バイアスとバリアンスのトレードオフ
横軸の左端は、モデルのパラメータをできるだけなくして訓練データにはほとんど適合していない(=バイアスが大きくバリアンスが小さい)ような単純すぎるモデル(例えば非常にシンプルな水平線など)であることを意味する。また、その右端は、パラメータをできるだけ多く持ち訓練データに完全に適合する(=バリアンスが大きくバイアスが小さい)ような複雑すぎるモデル(例えば非常に高次の多項回帰式など)であることを意味する。
※前述の通り、汎化誤差はバイアス+バリアンスだけでなくノイズも付加される点に注意。最適解を得るには、その汎化誤差を最小化する必要がある。
ちなみに、バイアスとバリアンスという2つの予測誤差を同時に最小化したいわけだが、これらは前述の通りトレードオフの関係にあり、相反する2つのことの板挟み状態であるため、その状態は「バイアスとバリアンスのジレンマ(Bias-Variance Dilemma)」とも呼ばれる。
- 参考文献1:『Pattern Recognition and Machine Learning』の147-152ページ
- 参考文献2:「Understanding the Bias-Variance Tradeoff」
Copyright© Digital Advantage Corp. All Rights Reserved.