シンプソンのパラドックス（Simpson's paradox）とは？：AI・機械学習の用語辞典

用語「シンプソンのパラドックス」について説明。主に層別の分割表において、グループ間に見られる相関関係が「全体でも成り立つだろう」と直感的に推測されるのに対し、場合によっては、全体では異なる結果になる現象を指す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　シンプソンのパラドックス（Simpson's paradox）とは、主にデータをいくつかのグループ（層）に分割した表において、グループ間に見られる相関関係（前提）が「全体でも成り立つだろう」と直感的に推測されるのに対し、場合によっては、実際にデータ全体に見られる相関関係（結果）が前提とは真逆になってしまう（もしくは一致しない）というパラドックス（逆説）現象を指す。統計学の用語である。その原因としてよくあるのは、各グループの個体数（サンプルサイズ）が大きく異なることだ。……という説明文だけだと分かりづらいと思われるので、次節で具体例を出してあらためて説明する。

図1　シンプソンのパラドックスのイメージ

　このシンプソンのパラドックスは、1951年に発表された統計学者のEdward H. Simpson（エドワード・シンプソン）氏による論文で最初に提示され、1972年に統計学者のColin R. Blyth（コリン・ブライス）氏による論文「On Simpson's Paradox and the Sure-Thing Principle」で命名された。同様の現象については、1900年前後に統計学者のKarl Pearson（カール・ピアソン）氏やUdny Yule（ウドニー・ユール）氏なども観察しているため、ユール゠シンプソン効果（Yule–Simpson effect）と呼ばれることもある。

　特に表データでグループ間に見られる相関関係から結論を導く際には、シンプソンのパラドックスになっていないかを注意する必要があるだろう。例えば「投薬が有益か無益か」を判断する際に、投薬したグループ間に見られる相関関係だけを見ていると結論を誤る可能性がある。

具体例

　例えば高校Aグループと高校Bグループのテスト結果を見比べて、どちらがより優秀な成績を出せるかを考えてみよう。各高校における男子と女子の平均点を表1にまとめた。

	男子	女子
高校A	90点	70点
高校B	85点	60点
表1　各高校における男子と女子の平均点

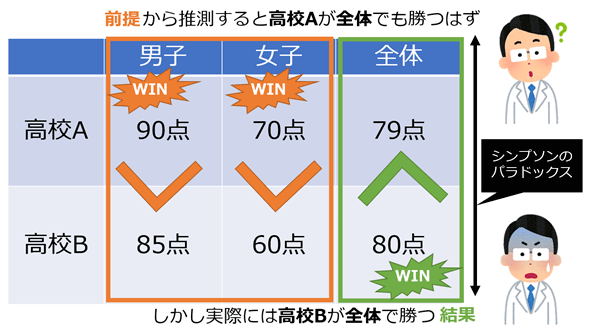
　表1を見ると、男子のテスト結果（平均点）は高校Aが90点で高校Bが85点で、高校Aの方が成績がよい。また女子のテスト結果（平均点）は高校Aが70点で高校Bが60点で、こちらも高校Aの方が成績がよい。両方とも高校Aの方が成績がよいので（前提）、「全体でも高校Aの方が成績がよいだろう」と直感的に推測される。しかしながら全体の平均点は表2の通りだ。

	男子	女子	全体
高校A	90点	70点	79点
高校B	85点	60点	80点
表2　各高校における全体の平均点

　男子と女子を合わせた全体のテスト結果（平均点）は高校Aが79点で高校Bが80点なので、先ほどの推測とは異なり高校Bの方が成績がよいという結果が出た。前提に基づく直感的な予測と、実際の結果が異なっている、この現象を「シンプソンのパラドックス」と呼ぶのである。

　なぜこうなるのか納得がいかないという人もいるだろう。この例においてパラドックスが生まれる原因は、各グループの個体数が異なることにある。具体的には表3のような人数構成となっている。

	男子	女子	全体
高校A	45人	55人	100人
高校B	80人	20人	100人
表3　各高校における男子と女子の人数構成

　高校Aはやや女子が多く、高校Bは圧倒的に男子が多い。各高校の全員分の合計点を算出すると、表4のようになる。

	男子の合計点	女子の合計点	全体の平均点（＝合計／人数）
高校A	4050点（＝90点×45人）	3850点（＝70点×55人）	79点（＝7900点／100人）
高校B	6800点（＝85点×80人）	1200点（＝60点×20人）	80点（＝8000点／100人）
表4　各高校における男子と女子の人数構成

　確かに最終的な平均点は高校Aが79点で高校Bが80点となることが確認できた。

「AI・機械学習の用語辞典」