[文章生成]PyTorchのRNNクラスを使って文章生成を行う準備をしよう:作って試そう! ディープラーニング工作室(2/2 ページ)
青空文庫から取得した小説データのインデックスへの変換、インデックスのベクトル化、RNNへの入力など、文章生成の準備と全体の流れを確認します。
形態素のベクトル化
既に述べましたが、上で作成したインデックス列はさらにベクトル化する必要があります。ベクトル化とは、特定の単語(あるいは形態素)のインデックスをn次元の実数ベクトルで表現することです。「n次元の実数空間に単語を埋め込む」ということからこれを「埋め込み」「embedding」などと表現することもあります。
形態素をベクトル化することには、単語間の結び付きをベクトルで表現できることや、語彙数(辞書の要素数)が膨大な量になった場合でも指定した次元数のベクトルとして表現できることから計算量を削減できるといったメリットがあります。こうした情報やベクトル化の方法などについては「挑戦! word2vecで自然言語処理(Keras+TensorFlow使用)」などを参照してください。
ここでは深く考えずに、上で作成したインデックス列をベクトル化して、それをRNNに入力してみると出力がどうなるかということを見ていくことにしましょう。
ここではPyTorchが提供しているEmbeddingクラスを利用してみます。その前に、データローダーから上で生成したデータセットのデータを読み込めるようにしておきましょう。
BS = 2
dl = DataLoader(dataset, batch_size=BS, shuffle=True, drop_last=True)
iterator = iter(dl)
X_train, y_train = next(iterator)
print(X_train.shape)
print(X_train)
print(y_train.shape)
print(y_train)
ここではバッチサイズを「2」として、DataLoaderクラスのインスタンスを生成しています。つまり、上で作成したデータセットから一度に2つずつ訓練データと正解ラベルを取得します。このコードを実行すると、次のような結果になります。
訓練データと正解ラベルの形状がどちらも「2×19」(バッチサイズ×要素数)となっている点に注目してください(先ほども述べたように、訓練データと正解ラベルをKajiiDatasetクラスの__init__メソッド内で作成するタイミングで、max_lengthで指定した値よりも要素数が1つ減っています)。
ここで、PyTorchのEmbeddingクラスのインスタンスを作ってみましょう。
VS = len(w2i) + 1 # vocabulary size
ED = 5 # embedding dimension
embedding = nn.Embedding(VS, ED, padding_idx=0)
Embeddingクラスのインスタンス生成時には、第1引数に辞書の要素数を、第2引数に埋め込みベクトルの次元数を指定します。また第3引数には上記のインデックス列でパディングに使っているインデックスを指定します。
辞書の要素数とはここでは最初に作成したいずれかの辞書の要素数でよさそうですが、実際にはパディング用の0が辞書にはキーとしても値としても含まれていません。そのため、上では定数VSに「len(w2i) + 1」のように「0」の分を加算しています。埋め込みベクトルの次元数(ED)については、ここでは少なめに「5」を指定しました。これは1つのインデックスが5次元の実数値で表されることを意味します。
このようにして作成したEmbeddingクラスのインスタンスに、先ほどデータローダーから取得した訓練データを渡して、その結果のデータや形状を確認してみましょう。
x = embedding(X_train)
print('X_train.shape:', X_train.shape)
print(X_train)
print('x.shape:', x.shape)
print(x)
print(i2w[14])
実行結果を以下に示します。
最初に出力されているのは元のテンソルの形状(2×19)を表します。次のテンソルは元のデータです。その次が、Embeddingクラスのインスタンスに元データを渡した結果、どんな形状のデータが返されたかを表しています。「2×19×5」と、元のテンソルよりも1つ次元が増えています。その下にあるテンソルがベクトル化されたデータです。
最初の要素を見ると、「9158」というインデックスが「[ 1.5599e-01, -8.2990e-01, -8.5238e-01, -3.7032e-01, 5.2685e-01]」という5次元のデータとして表現されているということです。単一の整数値だったものがベクトル化されているので、全体の次元数も1つ増えたというわけです。
ここで注目してほしいのは、「[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00]」というパディングされた埋め込みベクトルの上にある要素です。どちらも「[-2.3180e-01, -6.9880e-01, 7.8501e-01, -3.4193e-01, 2.5288e-02]」となっています。既に想像している方もいらっしゃるでしょうが、これは元データでいえばパディングに使った「0」の直前の要素、つまり「14」に対応するベクトルです。で、この「14」が何を表しているかを最後に表示しています。その結果は「。」です。多くの文が句点「。」で終わるので、これは納得です。
このように、同じ単語(形態素)は埋め込みによって同じ値を持つベクトルへと変換されるということです。そして、RNNにはこれらのベクトルが入力されることになります。
RNNへの入力
次に、上記の出力をRNNに入力してみましょう。まず、RNNクラスのインスタンスを生成します。
HS = 100 # hidden size
NM = 1 # num of layers for RNN
rnn = nn.RNN(input_size=ED, hidden_size=HS, batch_first=True, num_layers=1)
RNNへはベクトル化されて5次元のデータとなったインデックスを入力します。そのため、input_sizeは上で定義したED=5です。隠し状態(hidden_size)は適当にここではHS=100としました。レイヤ数(num_layers)はNM=1でよいでしょう。
このようにして作成したインスタンスには、入力(5次元のベクトル)と、そのバッチで使用する隠し状態の初期値を渡します。それがどんな形状のデータを出力するかを確認しましょう。
h = torch.zeros(NM, BS, HS)
r, h = rnn(x, h)
print('output from RNN:', r.shape)
実行結果は次のようになります。
RNNから出力されたデータは2×19×100となっています(100は隠し状態のサイズ)。
全結合層からの出力
後はこれを全結合層に入力して、その出力が辞書の語彙数(+1)となるようにするだけです。
fc = nn.Linear(HS, VS)
o = fc(r)
ここでは隠し状態のサイズが入力となり、出力数は辞書の語彙数(+1)です。この出力の結果をこれまでと同様に調べてみましょう。
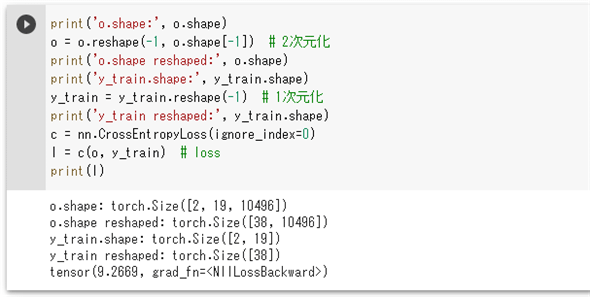
print('o.shape:', o.shape)
o = o.reshape(-1, o.shape[-1]) # 2次元化
print('o.shape reshaped:', o.shape)
print('y_train.shape:', y_train.shape)
y_train = y_train.reshape(-1) # 1次元化
print('y_train reshaped:', y_train.shape)
c = nn.CrossEntropyLoss(ignore_index=0)
l = c(o, y_train) # loss
print(l)
実行結果は以下の通りです。
全結合層からの出力は2×19×10496という形状になっています。「10496」というのは辞書の要素数+1です。これをreshapeメソッドで38×10496に変換しているのは、損失を計算するためです。一方、正解ラベルであるy_trainの形状も2×19となっているので、これもreshapeメソッドで1次元のデータへと変換しています。こうすることで、38個ある辞書のサイズの出力と、その出力に対するインデックスとを使って損失を計算できるようになるはずです。
RNNを使ってある形態素の次にくる形態素を推測して、その出力から損失を計算する全体的な流れは以上になります。次回は今見たような処理を行うクラスを定義して、実際に学習を行い、最後にうまい具合に文章が生成されるかを見ていくことにします。
消化不良という方もいらっしゃるかもしれないので、実際のクラスの定義だけ、ここで紹介しておきましょう。今回のノートブックには、次回にお話しする予定のコードも含まれているので、興味のある方はご覧ください(ただし、内容を変更する可能性はあります)。
class LangModel(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_size, batch_size=25, num_layers=1):
super().__init__()
self.hidden_size = hidden_size
self.batch_size = batch_size
self.num_layers = num_layers
self.device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=0)
self.rnn1 = nn.RNN(embedding_dim, hidden_size,
batch_first=True, num_layers=self.num_layers)
self.fc = nn.Linear(hidden_size, vocab_size)
self = self.to(self.device)
def init_hidden(self, batch_size=None):
if not batch_size:
batch_size = self.batch_size
self.hidden_state = torch.zeros(self.num_layers, batch_size,
self.hidden_size).to(self.device)
def forward(self, x):
x = self.embedding(x)
x, self.hidden_state = self.rnn1(x, self.hidden_state)
x = self.fc(x)
return x
Copyright© Digital Advantage Corp. All Rights Reserved.