積分法の数値計算をプログラミングしてみよう：数学×Pythonプログラミング入門（2/5 ページ）

積分法に関する数値計算のプログラミングの方法を見ていく。最初に台形公式やシンプソンの公式を使った方法を紹介し、次に乱数を使ったモンテカルロ法による近似方法を見る。

[羽山博，著]

目標2： シンプソンの公式を使って積分を行う

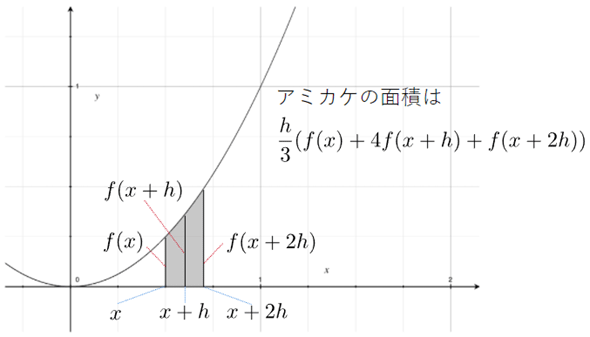
　台形公式では、曲線の部分を直線と見て近似値を求めるので若干の誤差が生じます。そこで、曲線の部分を二次式で近似するシンプソンの公式を使ってみましょう。シンプソンの公式を導き出すのは少し難しいので、ここでは割愛しますが、公式そのものは簡単です。図と合わせて見ておきましょう（図3）。

図3　シンプソンの公式を使って面積を求める
xを0から2hずつ動かしていきながら、中央の重みを大きくして平均を求めたものをアミカケ部分の面積とする。その面積を足していけば、全体の面積が求められる。

　図にも示してありますが、アミカケの部分の面積は、

で近似されます*1。xの値を2hずつ増やしていきながら、アミカケの部分の面積を足していけば全体の面積が求められます。

*1　この式は以前どこかで見たような気がしませんか。前回のルンゲクッタ法の式とよく似ていますね。実は、ルンゲクッタ法も、曲線を二次式で近似するという基本的な考え方はシンプソン法と同じです。

2. シンプソンの公式による積分をプログラミングする

　では、プログラミングに取りかかりましょう。数式さえ分かればもうお手のものですね。コードは以下の通りです。関数parabolicはリスト1と同じものですが、念のため再掲しておきます。

def parabolic(x):
  return x**2

リスト9　関数parabolicの定義（再掲）
y＝x²のグラフは放物線（parabolic）を描く。x²の値を返すだけなので関数の定義は簡単。

　シンプソンの公式により定積分を求める関数simpsonはリスト10のように定義されます。理解を確実にするため、穴埋め（ア／イ／ウ）にしておくので、ちょっと考えてみてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

import numpy as np

def simpson(func, xmin, xmax, h):
  result = 0
  w = h * 2
  for x in np.arange(xmin, xmax, w):
    result += (func(x) + 4*func(ア) + func(イ)) * (h / ウ)
  return result

リスト10　シンプソンの公式で定積分を求める関数simpsonの定義
（1）式の定義を素直にPythonの関数として表現し、全体の合計を求めるとよい。穴埋めでコードを完成させよう。

　答えは以下の通りです。オレンジ色の部分をクリックすると答えが表示されます。

• ア. 　x+h　
• イ. 　x+w　 （　x+2*h　でもよい）
• ウ. 　3　

　実行例は以下の通りです。

simpson(parabolic, 0, 1, 0.001)
# 出力例：0.3333333333333334

リスト11　シンプソンの公式で定積分の値を求めた結果
1/3＝0.333...とほぼ等しい結果となった。台形公式を使った場合より、はるかに誤差が小さいことが分かる。

　シンプソンの公式を使うと、非常に精度のよい積分の近似値が求められることが分かりました。では、次に、乱数を利用して確率や積分の近似計算を行うモンテカルロ法を見てみましょう。ここからは考え方が少し変わるので、一息ついてから次に進んでください。