[評価指標]混同行列(Confusion Matrix)とは?:AI・機械学習の用語辞典
用語「混同行列」について説明。陽性/陰性のどちらかに分類する二値分類のタスク(問題)に対する評価指標の計算式などで活用される4セル(=2行×2列)の分割表を指す。
用語解説
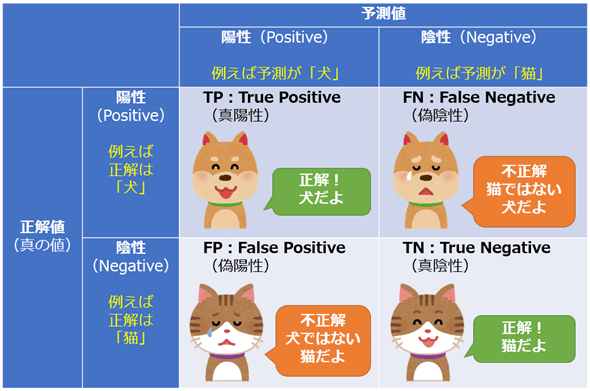
統計学/機械学習における混同行列(Confusion Matrix)とは、陽性(Positive)/陰性(Negative)のどちらかに分類する二値分類のタスク(問題)に対する評価指標の計算式などで活用される4セル(=2行×2列)の分割表で、1行目と2行目の行項目に「正解値×(陽性|陰性)」を、1列目と2列目の列項目に「予測値×(陽性|陰性)」を取る(図1)。※場合によっては、行と列の項目が逆の場合もあり、どちらでもよい。
先ほどは「陽性(Positive)」と表現したが、これは「状態あり」を意味し、機械学習では「正例」と表記される場合がある。また、「陰性(Negative)」は「状態なし」を意味し、「負例」と表記される場合がある。また、先ほどは「正解値」と表現したが「真の値」などと表記される場合がある。
図1を見ると分かるように、4セルの各項目の意味は以下の通りである。
- 1行1列目はTP(True Positive:真陽性)=正解値が陽性(Positive)で、予測値が陽性(Positive)なので、正解(True)
- 1行2列目はFN(False Negative:偽陰性)=正解値が陽性(Positive)で、予測値が陰性(Negative)なので、不正解(False)
- 2行1列目はFP(False Positive:偽陽性)=正解値が陰性(Negative)で、予測値が陽性(Positive)なので、不正解(False)
- 2行2列目はTN(True Negative:真陰性)=正解値が陰性(Negative)で、予測値が陰性(Negative)なので、正解(True)
二値分類の結果を評価する際には、これらの4項目の件数を確認、比較することが好ましい。
その上で、正解率(Binary Accuracy)、適合率(Precision)、再現率(Recall)/感度(Sensitivity)、特異度(Specificity)、F値(F-measure、F-score)/F1スコア(F1-score)などの二値分類の評価関数を選択して計算することになる。これらの評価関数の計算式は、上記のTP/FN/FP/TNという4つの変数を使って表現されるのが一般的だ。各評価関数の内容については後日解説する(現時点では「機械学習の評価関数(二値分類用)の基礎を押さえよう」という記事を参考にしてほしい)。
なお混同行列は、二値分類だけでなく多クラス分類のタスクでも使われることがある。その内容について「多クラス分類の混同行列とは?」で説明している。
Copyright© Digital Advantage Corp. All Rights Reserved.