ドラッグストアの開店予想で足りなかったモノ:AI・データサイエンスで遊ぼう(2/2 ページ)
ドラッグストアの開店候補地を予測するニューラルネットワークモデルが出した答えは果たして使い物になるのか、いろいろと考えてみましょう。
汎化性能が足りないチェーンG
ところで、先ほど「緑色のピンはあまりあてにはならないかもしれません」と書いたのを覚えているでしょうか。その理由は汎化性能に難がありそうだからです。
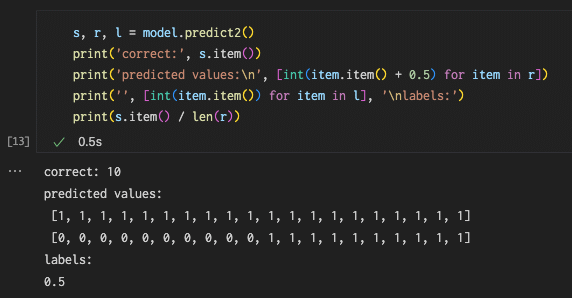
開店候補地を推測する3つのJupyterノートブックそれぞれでは、最初に教師ラベルが1のデータを10個と教師ラベルが0のデータを10個、合わせて20個のデータを汎化性能の評価用に確保しています(テストデータ)。下の画像は、このテストデータをチェーンGの開店候補地を推測するニューラルネットワークモデルに入力した結果です。
画像の「predicted values:」の下に推測された値を0か1に四捨五入したものを、その下に教師ラベルの値を表示しています。一目で分かりますが、なんと! 計20個のデータに対して、ニューラルネットワークモデルは全て1を出力しています。つまり、20個のテストデータが全て開店候補地になるとこの子は言い張っているのです。おかげで正解率は0.5になってしまいました。
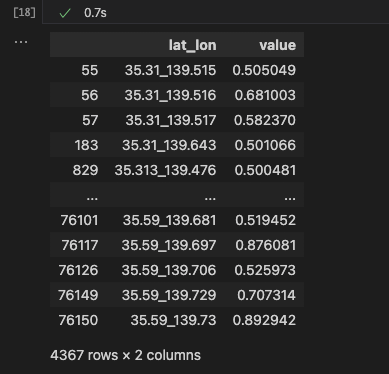
これってありがちな「何にでも1を返すヤツ」じゃない? と思うかもしれません。が、交差検証では各フォールドで80〜90パーセントを超える正解率で答えを出しているのです。ついでに横浜市を囲む範囲の周辺店舗情報を入力して、ニューラルネットワークモデルが計算した値で0.5以上のものがどのくらいかあるかを以下に示します。
約7万6000の位置に対して、0.5以上の値(四捨五入すると1になるもの)を算出したのは4400弱の箇所ということです。これは「何でもかんでも1を返せばいい」というモデルにはなっていないということです(0.9以上のものは、そのうちの約500カ所)。
この状況に対して、筆者自身が納得できる理由が見つからないというのが本当のところです。何となくこうなのかな? 仮説を一つひねり出すなら次のようなことが考えられるかもしれません。
チェーンGは大規模な駅の駅中や近所にも出店をしているし、私鉄沿線のそれほど大きくはないだろうという駅の周辺にも出店をしています。きめ細やかな店舗構成でいろいろなところに網を張って、人々のちょっとした買い物ニーズ(薬に限らず、細かな日用品や化粧品なども含む)に応えるというのがチェーンGの商売の仕方のように感じます。
こうしたことから、駅近隣の再開発に伴う一時閉店と同じ場所での再開店や近隣への移転もそれなりに行われているようです。筆者が見たところ、横浜近辺でそうした事象は4、5件あるようです(横浜近辺で閉店した店舗数は10程度なので、これはそれなりの割合といえるかもしれません)。こうした場合、閉店したときの周辺店舗情報がある程度維持されたまま、同じ場所あるいは近隣に再出店することで、よく似た周辺店舗情報に教師ラベル0と教師ラベル1の両方が付加される可能性はあります。
こうした傾向が全国的に見られるものであれば、閉店時の周辺店舗情報と同様なものがそれなりの数、開店時の周辺店舗情報としても存在することになり、これを学習したモデルに閉店時のデータを入力しても、これを開店候補地であると推測するかもしれません。
でもそれなら閉店した店舗の周辺店舗情報を入力したときに、開店と閉店の両方の予測が出そうな気もするので、やはりこれは理由として強くは推せません。何より、全国的にそうした傾向にあるとは思えません(日本全国で再開発が行われていて、そこにチェーンGが出店しているなんてことがあるでしょうか)。
そうなのではありますが、ニューラルネットワークモデルの隠れ層の数や重みの数など、パラメーターをいろいろといじっても、汎化性能が上がるポイントが見つからなかったので、今回については追求をあきらめておきましょう。
いいのか、それで(笑)。
正解率/適合率/再現率/F1スコアを計算してみよう
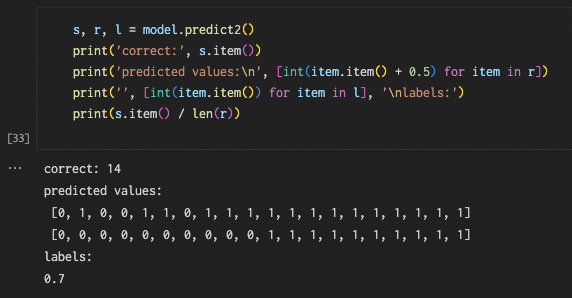
ちなみにチェーンRの汎化性能のテスト結果は次のようになっています。
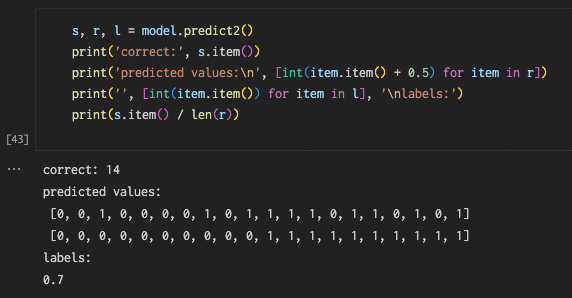
チェーンBでは次のようになっています。
どちらも正解率は0.7で「非常によい」というレベルには達していませんが、チェーンGに比べればよい結果です。チェーンRでは教師ラベル1のデータについては全て的中させて、教師ラベル0のデータについてはそれなりに間違っている(正解が4/10)のに対して、チェーンBではどちらもそれなりに間違っている(共に正解が7/10)のが2つのモデルの違いですね。
最後にチェーンR、G、Bのそれぞれについて、正解率(accuracy)、適合率(precision)、再現率(recall)、F1スコアを計算してみましょう。なお、これらの詳細については「機械学習の評価関数(二値分類用)の基礎を押さえよう」などを参照してください。
各チェーンの推測結果と教師ラベルを以下に示します(教師ラベルは全て同じです)。
| チェーン | 推測結果 |
|---|---|
| 教師ラベル | 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 |
| チェーンR | 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 |
| チェーンG | 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 |
| チェーンB | 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1 |
| 各チェーンの推測結果と教師ラベル | |
まずは、各チェーンについて以下を計算しておきます。
- TP(True Positive):教師ラベル1のデータを正しく「1」と推測した数
- TN(True Negative):教師ラベル0のデータを正しく「0」と推測した数
- FP(False Positive):教師ラベル0のデータを間違えて「1」と推測した数
- FN(False Negative):教師ラベル1のデータを間違えて「0」と推測した数
これを表にまとめると次のようになります。
| TP | TN | FP | FN | |
|---|---|---|---|---|
| チェーンR | 10 | 4 | 6 | 0 |
| チェーンG | 10 | 0 | 10 | 0 |
| チェーンB | 7 | 7 | 3 | 3 |
| チェーンごとのTP/TN/FP/FNの数 | ||||
上で既に見ましたが、正解率は「正解数/全データ数」=「(TP+TN)/(TP+TN+FP+FN)」で得られます。
- チェーンR:(10+4)/(10+4+6+0)=14/20=0.7
- チェーンG:(10+0)/(10+0+10+0)=10/20=0.5
- チェーンB:(7+7)/(7+7+3+3)=14/20=0.7
適合率は、教師ラベル1のデータを正しく推測できたかを示す値で「TP/(TP+FP)」で計算されます。つまり、教師ラベル1と推測したもののうち、実際に教師ラベルが1だったデータがどれだけあるかを知るためのものです。
- チェーンR:10/(10+6)=10/16=0.625
- チェーンG:10/(10+10)=10/20=0.5
- チェーンB:7/(7+3)=7/10=0.7
再現率は教師ラベル1のデータのうち、実際に教師ラベルが1であると推測できたものを示す値で、「TP/(TP+FN)」で算出されます(FNは教師ラベル1であるものを間違って0として予測したものの数)。
- チェーンR:10/(10+0)=10/10=1.0
- チェーンG:10/(10+0)=10/10=1.0
- チェーンB:7/(7+3)=7/10=0.7
適合率と再現率にはトレードオフの関係があり、その調和平均を算出したものがF1スコアと呼ばれる値です。これは「2×TP/(2×TP+FP+FN)」で計算されます。
- チェーンR:2 × 10/(2 × 10 + 6 + 0)=20/26=0.769
- チェーンG:2 × 10/(2 × 10 + 10 + 0)=20/30=0.667
- チェーンB:2 × 7/(2 × 7 + 3 + 3)=14/20=0.7
以上をまとめると次のようになります。
| 正解率 | 適合率 | 再現率 | F1スコア | |
|---|---|---|---|---|
| チェーンR | 0.7 | 0.625 | 1.0 | 0.769 |
| チェーンG | 0.5 | 0.5 | 1.0 | 0.667 |
| チェーンB | 0.7 | 0.7 | 0.7 | 0.7 |
| 各チェーンの正解率/適合率/再現率/F1スコア | ||||
これらの値は全て0〜1の範囲の値を取り、1に近いほどよいことを意味します。1になるにはFPとFNが0になる必要があります(つまり、全てのデータについて正しく推測できればよい)。また、TPとTNが0になれば(全ての推測が外れれば)これらの値は0になります。
チェーンRとBでは正解率が共に0.7ですが、正解の仕方が異なっていたことから他の値については異なる結果になっています。総合的にどちらがよいモデルなのかをハッキリということはできませんが、まあ、それなりといったところなのかもしれません。
少なくとも実運用するにはどちらも性能が足りていないでしょう。
チェーンGについては再現率が1.0なこと(教師ラベルが1であるデータについては、全て正解できたこと)についてはよかったのかもしれませんが、上でも見たようにこのモデルは何らかの理由で閉店時の周辺店舗情報についても開店時のもの(教師ラベルが1)だと推測をしてしまっています。このことから他の値については軒並みよくない数値となっているので、今後(があるのなら)改善したり最初からやり直したりする必要があるでしょう。
本企画では3回にわたってドラッグストアチェーンの開店候補地の予測にまつわる話をしてきました。予測を行うモデルを作成する中で筆者は、不均衡データの扱い、データの前処理はとても大事、JupyterノートブックとPythonスクリプトのすみ分け、交差検証や汎化性能の検証も重要といったことを体感しました。やはり、自分で何かを作ってみる、作りながら問題にぶつかって解決してみるのは面白いし、いろいろな学びを得られますね。
今回は自分たちの手元にあるデータで何かできないかという出発点から開店候補地の予測をしてみましたが、Kaggleならさまざまな分野のさまざまな課題が既に用意されているので、近いうちにまたKaggleに復帰して、何か試してみたいなぁと感じました。
確かに不均衡データを初め、私にとっても勉強になることが多かったです。「データがある→目的を考える」というのはデータサイエンスやAIの領域では本末転倒で嫌われるスタート地点で、「何をしたいか→データを集める」という流れであるべき、とよく言われていると思いますが、「身近なデータがある→何らかのAIを作る」という流れだったとしても今回のような「学び」などのメリットはありますね。
Copyright© Digital Advantage Corp. All Rights Reserved.