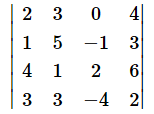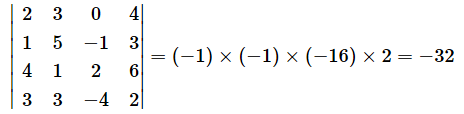[AI・機械学習の数学]線形代数の行列式をマスター:AI・機械学習の数学入門(1/3 ページ)
連載の通常の流れとは別の番外編。ベクトルや行列の四則演算から内積あたりまでは比較的スムーズに理解できるのだが、突如、行列式や固有値、固有ベクトルといった謎キャラが登場して挫折してしまう、というのはありがちな話。統計学や機械学習のさまざまな手法の背景にあるこれらの考え方を見ていきたい。
行列式や固有値、固有ベクトルの壁を越えられないのは、行と列を掛けたり足したりという成分の計算で力を使い果たしてしまい、図形的な意味や線形代数の体系の中での意味を考える余裕がないからではないでしょうか。今回は行列式について、計算で力尽きないようにするための裏技を見た後、図形的な意味などについて考えてきたいと思います。固有値、固有ベクトルについては番外編5で取り扱います。
ポイント1 行列式はスカラーである
まず、大前提です。行列式が求められるのは行数と列数が同じ正方行列のみです。ここからのお話に登場する行列は全て正方行列です。
さて、2×2行列の行列式は平行四辺形の面積を表すとか、3×3の行列式は平行六面体の体積を表すといった話を聞いたことがある人も多いかと思います。面積とか体積であるということは、行列式はスカラーであるということです。
行列Aの行列式はdet Aまたは|A|と表します。detはdeterminantの略です。
例えば、
の行列式は、4×1−3×(−2)=10です。この計算を一般的に書くと、以下のようになります。
のとき、
2×2行列の場合はこれで計算できますが、3×3行列の行列はサラスの公式(後述)を使って計算します。掛けたり足したり(引いたり)する順序が複雑なので、このあたりで嫌気が差してしまう人も多いかもしれませんが、それは多くの教科書に掲載されている図解が不親切だからです。次のポイント2に示す方法を使ってやってみるとすぐにできるようになります。さらに、何次の行列であっても簡単に行列式の値が求められる方法もその後で見ます。
ポイント2 3次以上の行列式を簡単に求めるには上三角行列を作る
まず、サラスの公式による3×3行列の行列式の求め方を示しておきます。一般的な教科書では、1つの図にまとめてあるので、あっちに行ったりこっちに来たりと、ややこしくなっていますが、図1のように、作業用に同じ行列式を下に書いておき、ステップを分ければスッキリします。
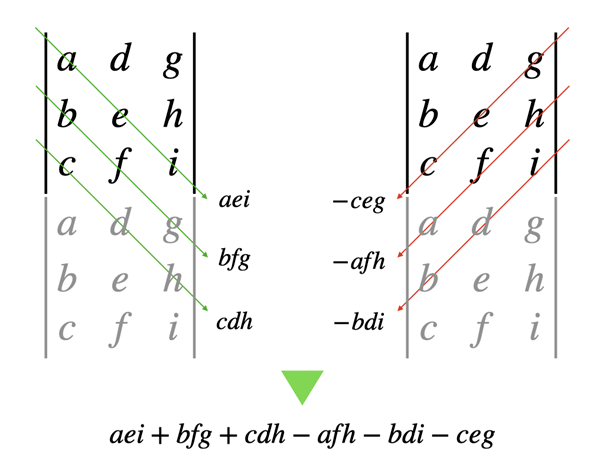
図1 サラスの公式による3×3行列の行列式の求め方
作業用に同じ行列式を下に書き、ステップを分けて考えるとよい。左上から始めて、右下に向けて積を求めたものが足していく項、次に右上から始めて、左下に向けて積を求めたものが引いていく項になる(最後に示した式ではアルファベット順になるように項の順序を整理してある)。
3次の行列式だとこれでできますね。しかし、4次以上になると、この方法は使えません。どうなるかのも想像できませんね。そこで、とっておきの裏技を紹介しましょう――ExcelのMDETERM関数を使うか、PythonのプログラムであればNumPyのlinalg.det関数を使う、です!……というのは半分冗談ですが(といっても、最も実用的な方法です)、やはり、数学的な手法や意味を理解しておきたいところです。
行列式の以下の性質についてはすでに分かっているものとしましょう。なぜそうなるのかは後で図解しますが、これらの性質を使います。
- 行を入れ替えると行列式の符号が反転する
- ある行に定数cを掛けると、行列式の値がc倍される
- ある行に定数cを掛けたものを、ほかの行に足しても行列式の値は変わらない
これらの性質は行だけでなく列の入れ替えや列の定数倍などについても同じです。
まず、上三角行列の行列式が対角成分の積になっていることを確認しましょう。上三角行列とは、対角成分の下が全て0である行列のことです。
図1のサラスの公式による行列式の求め方と使っている文字が異なりますが、公式に当てはめるまでもなく、対角成分のabc(図1ではaeiとなっている)以外の矢印は全て0を通ることが分かります。従って、対角成分の積のabcだけが残るというわけです。
ということは、上に示した性質を使って、行列式を上三角行列の形に変形すれば行列式が簡単に求められるはずです。
そこで、4次の行列式の値を計算してみます。最初は、行列式の値を変えずに1行1列目の下を全て0にすることを目標に進めます。以下の例でやってみましょう。
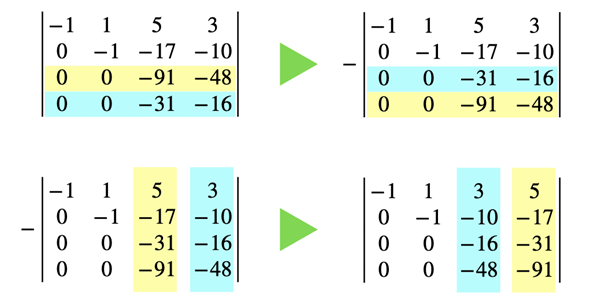
まず、1行目と2行目を入れ替えます。行を入れ替えると符号が反転するので、以下のようになります。ここからは細かなステップで少しずつ進めるので、ちょっと長くなります。ゆっくり確実に読み進めていってください。
ここで、1列目と3列目を入れ替えましょう。列を入れ替えたので、また符号が反転します。以下のように、2行1列目を0にできました。
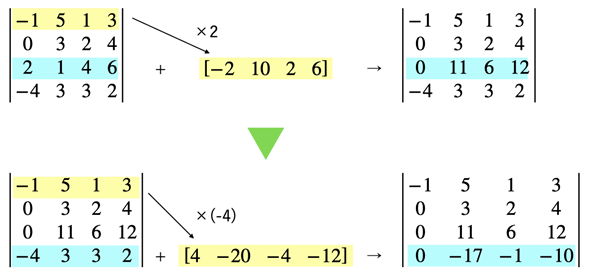
次に、1行目を2倍した[-2 10 2 6]を3行目に足し、1行目を-4倍した[4 -20 -4 -12]を4行目に足します。「ある行に定数cを掛けたものを、ほかの行に足しても行列式の値は変わらない」という性質を利用したので、行列式の値は変わりません。これで、1行1列目の下が全て0になります。
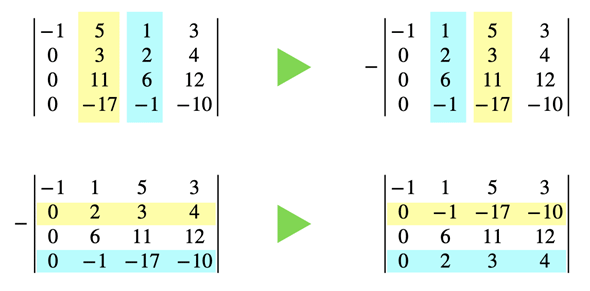
続いて、2行2列目の下を全て0にすることを目標にします。この後の計算をしやすくするために、2列目と3列目を入れ替え、さらに2行目と4行目を入れ替えておきます。符号が2回反転するので、元に戻ります。
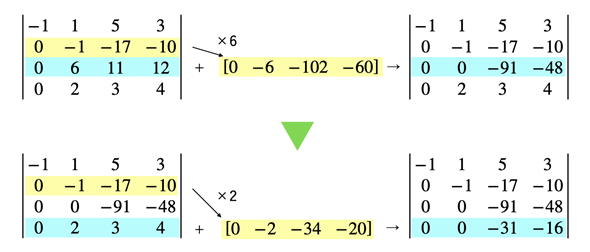
2行目を6倍した[0 -6 -102 -60]を3行目に足し、2行目を2倍した[0 -2 -34 -10]を4行目に足しましょう。やはり行列式の値は変わりません。
最後は4行3列目の-31を0にすればいいですね。3行目を-91/31倍したものを4行目に足してもいいのですが、-48が-16で割り切れることに気づけば、行と列の入れ替えをしておいた方が計算が簡単になります。3行目と4行目を入れ替えた後、3列目と4列目を入れ替えます。符号は2回反転するので元のままです。
3行目を-3倍した[0 0 48 93]を4行目に足します。これで上三角行列の形になりました。
対角要素を掛ければ行列式の値が求められます。
というわけで、計算しやすい単純な形に行列式を変形していけば、効率よく行列式が求められることが分かりました。行や列の入れ替えを行わず、(分数の出現をものともせず)強引に計算していってもいいのですが、多少の洞察力を働かせば、計算も楽にできますね。
ところで、結果を見ると負の値になっています。最初に、2×2の行列式は平行四辺形の面積で、3×3の行列式は平行六面体の体積であるというお話をしましたが、面積や体積が負の値になるというのはどういうことでしょうか(上の例は4×4行列なので、図形として表すのは難しいですが、やはり4次元空間での体積に当たるものです)。
そこで、行列式の図形的な意味を確認しておきましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.