[解決!Python]集合の要素を操作するには:解決!Python
集合の要素数を調べたり、集合と集合の包含関係を調べたり、集合と集合から和/差/交差/対称差からなる新たな集合を得たりする方法を紹介する。
# sの要素数を調べる
s = {0, 1, 2, 3}
l = len(s)
print(l) # 4
# sに要素xが含まれているかどうかを調べる
print(1 in s) # True
print(5 in s) # False
# sに要素xが含まれていないかかどうかを調べる x not in s
print(1 not in s) # False
print(5 not in s) # True
# s1とs2が同じ(要素のみを含んでいる)かどうかを調べる
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 == s2) # True
# s1とs2が異なるかどうかを調べる
s1, s2 = {0, 1, 2}, {0, 1, 3}
print(s1 != s2) # True
# s1とs2が互いに素かどうかを調べる
s1, s2 = {0, 1, 2}, {3, 4, 5}
print(s1.isdisjoint(s2)) # True
s1, s2 = {0, 1, 2}, {2, 3, 4}
print(s1.isdisjoint(s2)) # False
# どちらかの集合がもう一方の集合に包含されるかどうかを調べる
s1, s2 = {0, 1, 2, 3}, {0, 2}
print(s1.issubset(s2)) # False
print(s2.issubset(s1)) # True
print(s2 <= s1) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 <= s2) # True
# s1がs2の真部分集合かどうかを調べる
s1, s2 = {0, 1, 2}, {0, 1, 2, 3}
print(s1 < s2) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 < s2) # False
# どちらかの集合がもう一方の集合を包含するかどうかを調べる
s1, s2 = {0, 1, 2, 3}, {0, 1, 2}
print(s1.issuperset(s2)) # True
print(s2.issuperset(s1)) # False
print(s1 >= s2) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 >= s2) # True
# s1がs2の真上位集合かどうかを調べる
s1, s2 = {0, 1, 2, 3}, {0, 1, 2}
print(s1 > s2) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 > s2) # False
# s1とs2の和からなる集合を作成する
s1, s2 = {0, 1, 2}, {1, 2, 3}
result = s1.union(s2)
print(result) # {0, 1, 2, 3}
print(s1) # {0, 1, 2}
result = s1 | s2
print(result) # {0, 1, 2, 3}
print(s1) # {0, 1, 2}
s3 = {3, 4, 5}
result = s1 | s2 | s3
print(result) # {0, 1, 2, 3, 4, 5}
# s1とs2の差からなる集合を作成する
s1, s2 = {0, 1, 2, 3, 4, 5}, {1, 3, 5}
diff = s1.difference(s2)
print(diff) # {0, 2, 4}
s1, s2 = {0, 1, 2, 3, 4, 5}, {0, 2, 4}
diff = s1 - s2
print(diff) # {1, 3, 5}
# s1とs2の交差からなる集合を作成する
s1, s2 = {0, 1, 2, 3}, {2, 3, 4, 5}
intersection = s1.intersection(s2)
print(intersection) # {2, 3}
intersection = s1 & s2
print(intersection) # {2, 3}
# s1とs2の対称差からなる集合を作成する
s1, s2 = {0, 1, 2, 3, 4, 5}, {3, 4, 5, 6, 7, 8}
symdiff = s1.symmetric_difference(s2)
print(symdiff) # {0, 1, 2, 6, 7, 8}
s1, s2 = {0, 1, 2, 3, 4, 5}, {4, 5, 6, 7, 8, 9}
symdiff = s1 ^ s2
print(symdiff) # {0, 1, 2, 3, 6, 7, 8, 9}
集合に対する操作
以下に集合で行える各種操作を一覧する。表中に出てくるs/s1/s2は全て何らかの要素を含んだ集合オブジェクトとする。
| 操作 | メソッド/演算子 |
|---|---|
| sの要素数を調べる | len(s) |
| sに要素xが含まれているかどうかを調べる | x in s |
| sに要素xが含まれていないかかどうかを調べる | x not in s |
| s1とs2が同じ(要素のみを含んでいる)かどうかを調べる | s1 == s2 |
| s1とs2が異なるかどうかを調べる | s1 != s2 |
| s1とs2が互いに素かどうかを調べる | s1.isdisjoint(s2) |
| s1がs2に包含されるかどうかを調べる | s1.issubset(s2) s1 <= s2 |
| s1がs2の真部分集合かどうかを調べる | s1 < s2 |
| s1がs2を包含するかどうかを調べる | s1.issuperset(s2) s1 >= s2 |
| s1がs2の真上位集合かどうかを調べる | s1 > s2 |
| s1とs2の和集合を作成する | s1.union(s2) s1 | s2 |
| s1とs2の交差を作成する | s1.intersection(s2) s1 & s2 |
| s1からs2の要素を削除した差集合を作成する | s1.difference(s2) s1 - s2 |
| s1とs2の対称差集合を作成する | s1.symmetric_difference(s2) s1 ^ s2 |
| 集合に対する操作 | |
以下では、これらの操作を幾つかの分野に分けて見ていく。
基本
リストなどの反復可能オブジェクトと同様に、集合の要素数はlen関数で調べられる。また、特定の要素が集合に含まれているか/含まれていないかはin演算子/not in演算子で調べられる。2つの集合が同じか(同じ要素だけを含んでいるか)どうかは==演算子や!=演算子で調べられる。
以下に例を示す。
# sの要素数を調べる
s = {0, 1, 2, 3}
l = len(s)
print(l) # 4
# sに要素xが含まれているかどうかを調べる
print(1 in s) # True
print(5 in s) # False
# sに要素xが含まれていないかかどうかを調べる x not in s
print(1 not in s) # False
print(5 not in s) # True
# s1とs2が同じ(要素のみを含んでいる)かどうかを調べる
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 == s2) # True
# s1とs2が異なるかどうかを調べる
s1, s2 = {0, 1, 2}, {0, 1, 3}
print(s1 != s2) # True
包含関係のチェック
ある集合s1とs2があったとすると、それらには包含関係が成り立つことがある。集合s1の要素が集合s2の要素と全く同じであれば、それらの集合は等しい。
また、集合s1が集合s2の全ての要素を含んでいれば、集合s1は集合s2を「包含」している。このとき、集合s1は集合s2の「上位集合」(superset)であり、集合s2は集合s1の「部分集合」(subset)である。さらに集合s1には集合s2に含まれていない要素があるのであれば、集合s1は集合s2の「真上位集合」であり、集合s2は集合s1の「真部分集合」となる。
一方、集合s1と集合s2の間で共通する要素が1つもないような場合、それらの集合は「互いに素」という。このような集合同士の関係を調べるためにPythonでは以下のようなメソッドおよび演算子が用意されている(表中のs1とs2は共に何らかの集合を表す)。
| 操作 | メソッド/演算子 |
|---|---|
| s1とs2が互いに素かどうかを調べる | s1.isdisjoint(s2) |
| s1がs2に包含されるかどうか(s1がs2の部分集合かどうか)を調べる | s1.issubset(s2) s1 <= s2 |
| s1がs2の真部分集合かどうかを調べる | s1 < s2 |
| s1がs2を包含するかどうか(s1がs2の上位集合かどうか)を調べる | s1.issuperset(s2) s1 >= s2 |
| s1がs2の真上位集合かどうかを調べる | s1 > s2 |
| 集合と集合の関係を調べるメソッド/演算子 | |
以下はisdisjointメソッドを使って、2つの集合が互いに素であるかどうかを調べる例だ。
s1, s2 = {0, 1, 2}, {3, 4, 5}
print(s1.isdisjoint(s2)) # True
s1, s2 = {0, 1, 2}, {2, 3, 4}
print(s1.isdisjoint(s2)) # False
最初の例では{0, 1, 2}と{3, 4, 5}という共通する要素がない(つまり、互いに素な)2つの集合を比べているので結果はTrueとなる。2つ目の例では共通する要素があるので結果はFalseとなる。
次は{0, 1, 2, 3}という集合と{0, 2}という集合があったときに、どちらかがどちらかの部分集合であるかどうかをissubsetメソッドと<=演算子で調べる例だ。
s1, s2 = {0, 1, 2, 3}, {0, 2}
print(s1.issubset(s2)) # False
print(s2.issubset(s1)) # True
print(s2 <= s1) # True
issubsetメソッドの呼び出しに使用した集合が、引数に指定した集合の部分集合なら結果はTrueとなる。<=演算子の場合は、演算子の左側の集合が右側の集合の部分集合であるときに結果がTrueとなる。なお、issubsetメソッドも<=演算子も2つの集合が同一である場合にもTrueとなる(以下は<=演算子での例)。
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 <= s2) # True
そうではなく、どちらかがどちらかの真部分集合であるかどうかを調べるのなら、<演算子を使用する。
s1, s2 = {0, 1, 2}, {0, 1, 2, 3}
print(s1 < s2) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 < s2) # False
最初の例では、{0, 1, 2}という集合が{0, 1, 2, 3}の真部分集合であるかどうかを調べているので、結果はTrueとなる。次の例では、{0, 1, 2}という同じ要素からなる2つの集合を比べているので<=演算子のときとは異なり、結果はFalseとなる。
同様に、一方の集合がもう一方の集合を包含しているかどうかはissupersetメソッド、>=演算子、>演算子を使って調べられる。以下に例を示す。説明は不要だろう。
# どちらかの集合がもう一方の集合を包含するかどうかを調べる
s1, s2 = {0, 1, 2, 3}, {0, 1, 2}
print(s1.issuperset(s2)) # True
print(s2.issuperset(s1)) # False
print(s1 >= s2) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 >= s2) # True
# s1がs2の真上位集合かどうかを調べる
s1, s2 = {0, 1, 2, 3}, {0, 1, 2}
print(s1 > s2) # True
s1, s2 = {0, 1, 2}, {0, 1, 2}
print(s1 > s2) # False
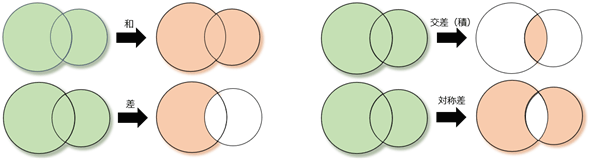
2つ以上の集合から集合を新たに作成する
2つ以上の集合を基に和、差、交差(積)、対称差という新たな集合を作成できる。
これらを作成するメソッドと演算子を以下に示す。
| 操作 | メソッド/演算子 |
|---|---|
| s1とs2の和集合を作成する | s1.union(s2) s1 | s2 |
| s1とs2の交差を作成する | s1.intersection(s2) s1 & s2 |
| s1からs2の要素を削除した差集合を作成する | s1.difference(s2) s1 - s2 |
| s1とs2の対称差集合を作成する | s1.symmetric_difference(s2) s1 ^ s2 |
| 和/差/交差/対称差を作成するメソッド/演算子 | |
以下は{0, 1, 2}という集合と{0, 1, 2, 3}という集合の和からなる集合を新たに作成する例だ。
s1, s2 = {0, 1, 2}, {1, 2, 3}
result = s1.union(s2)
print(result) # {0, 1, 2, 3}
print(s1) # {0, 1, 2}
result = s1 | s2
print(result) # {0, 1, 2, 3}
print(s1) # {0, 1, 2}
最初の例ではunionメソッドを使用している。次の例では|演算子を使用している。これらのメソッド/演算子は新たに集合を作成する点は覚えておこう。もともとの集合は変化しない。また、|演算子を連続することで、3つ以上の集合の和を計算することもできる(こうした特性は他の演算子でも同様)。
s3 = {3, 4, 5}
result = s1 | s2 | s3
print(result) # {0, 1, 2, 3, 4, 5}
以下はdifferenceメソッドと-演算子を使って、2つの集合の差からなる集合を作成する例だ。
s1, s2 = {0, 1, 2, 3, 4, 5}, {1, 3, 5}
diff = s1.difference(s2)
print(diff) # {0, 2, 4}
s1, s2 = {0, 1, 2, 3, 4, 5}, {0, 2, 4}
diff = s1 - s2
print(diff) # {1, 3, 5}
最初の例では集合s1({0, 1, 2, 3, 4, 5})から集合s2({1, 3, 5})に含まれている要素を除いたものが差となる。2つ目の例では集合s2が{0, 2, 4}となっているので、その要素を集合s1から取り除いたものが差となる。
以下はintersectionメソッドと&演算子を使って、交差からなる集合を新たに作成する例だ。交差は2つの集合に共通する要素からなるので、この場合は{2, 3}という集合が新たに作成される。
s1, s2 = {0, 1, 2, 3}, {2, 3, 4, 5}
intersection = s1.intersection(s2)
print(intersection) # {2, 3}
intersection = s1 & s2
print(intersection) # {2, 3}
最後に、symmetric_differenceメソッドと^演算子を使って、対称差を求める例だ。対称差とは2つの集合でいずれかの集合にしか存在しない要素のこと(2つの集合で共通する要素を取り除いたもの)。
s1, s2 = {0, 1, 2, 3, 4, 5}, {3, 4, 5, 6, 7, 8}
symdiff = s1.symmetric_difference(s2)
print(symdiff) # {0, 1, 2, 6, 7, 8}
この例ではsymmetric_differenceメソッドを使用している。2つの集合は{0, 1, 2, 3, 4, 5}と{3, 4, 5, 6, 7, 8}なので、対称差は共通する要素を取り除いた{0, 1, 2, 6, 7, 8}となる。
以下は^演算子を使用する例だ。
s1, s2 = {0, 1, 2, 3, 4, 5}, {4, 5, 6, 7, 8, 9}
symdiff = s1 ^ s2
print(symdiff) # {0, 1, 2, 3, 6, 7, 8, 9}
この例では2つの集合は{0, 1, 2, 3, 4, 5}と{4, 5, 6, 7, 8, 9}なので対称差は{0, 1, 2, 3, 6, 7, 8, 9}となる。
Copyright© Digital Advantage Corp. All Rights Reserved.