幾何平均とは? 算術平均との違い、使い分け:AI・機械学習の用語辞典
用語「幾何平均」について説明。幾何平均はデータの各数値を掛け合わせた積のn乗根(nはデータ数)を取った値を表す。時間に応じて変化する変化率/比率/倍率のデータ(=乗算後に累積される乗法的なデータ)を平均する場合に適した平均の計算方法だ。
用語解説
最も一般的に使われる「平均」とは、全ての数値を足して合計し、それを数値の総数で割ることである。これは、数学/統計学/機械学習において「算術平均」と呼ばれる。平均には他にも、「加重平均」や「幾何平均」「調和平均」「トリム平均」「移動平均」などがある。本稿ではこれらのうち幾何平均について解説する。なお算術平均については、「平均値(Mean)/中央値(Median)/最頻値(Mode)とは?」で説明しているので併せて参照してほしい。
数学/統計学/機械学習における幾何平均(Geometric Mean)とは、n個あるデータの各数値を全て掛け合わせた積(総乗値)のn乗根*1を取ることである。幾何平均は相乗平均とも呼ばれる。
*1 nはデータの数であり、n=2(つまり√)のときは「平方根」、n=3(つまり3√)のときは「立方根」、n=4(つまり4√)のときは「4乗根」、それ以降も「5乗根」「6乗根」……といったように呼び、これらをまとめて「累乗根」と呼ぶ。n乗根とは、n乗したら指定した数値(この数値が√の中にある)になる数を求める操作である。このとき、一般にn√という記号を用いる。ルート(root:√)を訳すと「根」になり、√記号は「根号」とも呼ぶ。
以下では「算術平均と何が違うのか」が分かるように、算術平均と幾何平均の計算方法と数学公式を紹介し、最後に使い分け指針をまとめる。計算方法の説明は冒頭の説明の繰り返しになるが、公式の意味を分かりやすくするために記述したので、ご了承いただきたい。
算術平均
算術平均(Arithmetic Mean)値とは、データの各数値(xiは、数値1, 数値2, ..., 数値nのいずれかの数値)を全て足した合計値をデータ数(n)で割った値のことである。算術平均は相加平均とも呼ばれる。数学の公式は以下のようになる。
算術平均は、最も一般的な「平均」の計算方法で、通常はこれを使えばよい。例えば月ごとの平均気温を求めたり、英語の試験の平均点を求めたりするのに使える。
幾何平均
幾何平均(Geometric Mean)値とは、データの各数値(xiは、数値1, 数値2, ..., 数値nのいずれかの数値)を全て掛け合わせた積の値を、n乗根した値のことである。なお、データに負の値を含めることはできないので注意してほしい。数学の公式は以下のようになる(nはデータ数)。
幾何平均は、時間に応じて変化する変化率/比率/倍率のデータの平均値を求める場合に、算術平均の代わりに用いるとよい。例えば月ごとの人口増加率(変化率のデータ)の平均値を求めたり、年ごとの貯金利息率(比率のデータ)の平均値を求めたりするのに使える。
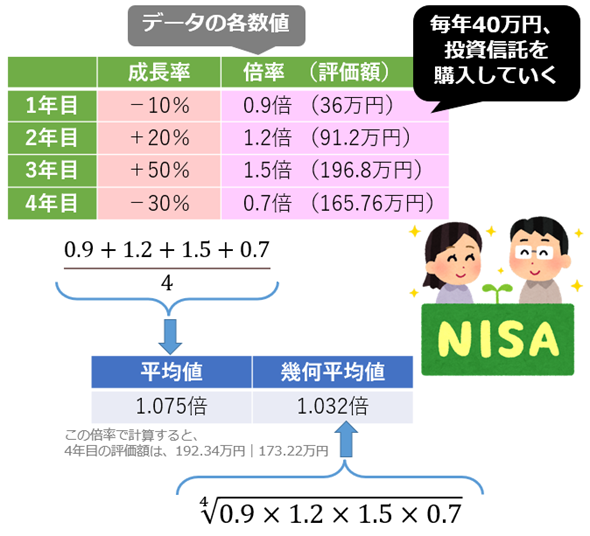
例えば、NISA(少額投資非課税制度)で毎年40万円の投資信託を4年間購入してきたとする。このケースで4年分の成長率の平均を取りたい場合、算術平均よりも幾何平均がより適切だ。実際に以下の数値例で幾何平均値を計算してみよう。
- 1年目の成長率: −10% 0.9倍 (評価額:36万円)
- 2年目の成長率: +20% 1.2倍 (評価額:91.2万円)
- 3年目の成長率: +50% 1.5倍 (評価額:196.8万円)
- 4年目の成長率: −30% 0.7倍 (評価額:165.76万円)
算術平均では、合計4.3倍(=0.9+1.2+1.5+0.7)を4年間で割ると、平均は1.075倍になる。これにより、年間平均で7.5%のリターンが得られたと解釈される。
幾何平均では、積(乗算)1.134倍(=0.9×1.2×1.5×0.7)の(4年間で)4乗根(=4√(1.134))を取ると、平均は約1.032倍になる。これにより、年間平均で3.2%のリターンが得られたと解釈される。
毎年40万円ずつ投資したので、投資額の合計は160万円である。4年目の投資信託の評価額(実態)は165.76万円になるので、4年間で5万7600円の含み益ではあるものの、成長率の数値が大きいにもかかわらず意外に増えていない結果となった。
まず、算術平均の年間平均で7.5%で4年目の投資信託の金額を以下のように算出すると、4年目の投資信託の評価額は192.34万円になるので、実態との乖離(かいり)は約26.58万円と大きい。
- 1年目の成長率: +7.5% 1.075倍 (評価額:43万円)
- 2年目の成長率: +7.5% 1.075倍 (評価額:約89.23万円)
- 3年目の成長率: +7.5% 1.075倍 (評価額:約138.92万円)
- 4年目の成長率: +7.5% 1.075倍 (評価額:約192.34万円)
次に、幾何平均の年間平均で3.2%で4年目の投資信託の金額を以下のように算出すると、4年目の投資信託の評価額は173.22万円になるので、実態との乖離(かいり)は約7.46万円とより小さい。
- 1年目の成長率: +3.2% 1.032倍 (評価額:41.28万円)
- 2年目の成長率: +3.2% 1.032倍 (評価額:約83.88万円)
- 3年目の成長率: +3.2% 1.032倍 (評価額:約127.85万円)
- 4年目の成長率: +3.2% 1.032倍 (評価額:約173.22万円)
このように変化率の平均を取る場合は、幾何平均の方がより実態を反映した平均値が求まる。
算術平均と幾何平均と調和平均の使い分け指針
「どういう場合にどちらの平均を採用すればよいか」は既に説明したが、以下に使い分け指針をまとめておく。
- 各数値が同じ重要度を持つデータを平均したい場合 → 算術平均
- 時間に応じて変化する変化率/比率/倍率のデータ(=乗算後に累積される乗法的なデータ)を平均したい場合 → 幾何平均
- 速度/レート(率)のデータ(=逆数の形で加算される加法的なデータ)を平均したい場合 → 調和平均
先ほどの成長率の計算は、1年目、2年目……と、現在の評価額に次々と掛け算していくことになるため、つまり「乗算後に累積される乗法的なデータ」であるため「幾何平均」が最適である。
一方、調和平均は後日解説予定だが、“率”を平均するのに向いている点が幾何平均と類似するので、ここでも比較対象として取り上げた。上ではレート(率)と書いたが、例えば2人の労働者がいて、1人目は1時間で10個の製品を作成し、2人目は1時間で5個の製品を作成する場合、全体の作業効率の平均値を計算するのに「調和平均」が適している。1人の作業効率として「1個を作るのに必要な時間」は時間/製品数で求まるので、1人目が1/10時間、2人目が1/5時間で、これらの調和平均は8分となる。この例では、作業効率(時間/製品数=製品数の逆数)が「逆数の形で加算される加法的なデータ」だから「調和平均」が適しているのである。
Copyright© Digital Advantage Corp. All Rights Reserved.