[データ分析]相関係数 〜 気温と電気代に関係はあるのか?:やさしいデータ分析
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第13回。変数同士の関係の強さを表す相関係数の計算内容を仕組みから理解します。Excelを使って手を動かしながら、相関係数の意味や求め方、落とし穴などについて学んでいきましょう。
連載:
この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト(ExcelやGoogleスプレッドシート)を利用した作成例を紹介します。
必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入(またもや金欠)。
前回は散布図やバブルチャートを作成して、「変数同士の関係」を可視化しました。
今回は、「変数同士の関係」を数値で表すことを考えてきます。相関係数は変数同士の関係の強さを表す値としてよく知られていますが、相関という言葉だけが一人歩きして、不適切な解釈や使われ方をすることもよくあります。
そこで、相関係数の求め方と意味を確認した後、ケーススタディを通して分析していきます。。その中で、相関係数に関する落とし穴についても解説します。相関係数(ピアソンの積率相関)は間隔尺度の変数同士で使われますが、順序尺度や名義尺度の場合に使われる、関係の強さを表す値(順位相関やクラメールの連関係数)についても最後に紹介します。
まず、問題提起です。図1をご覧ください。このデータは気温と家庭でのCO2排出量の値です(2021年度)。気温の出典は気象庁のページから札幌、東京、那覇の値を取り出したものです。CO2排出量の出典は、環境省による、北海道、関東甲信、沖縄のデータです。
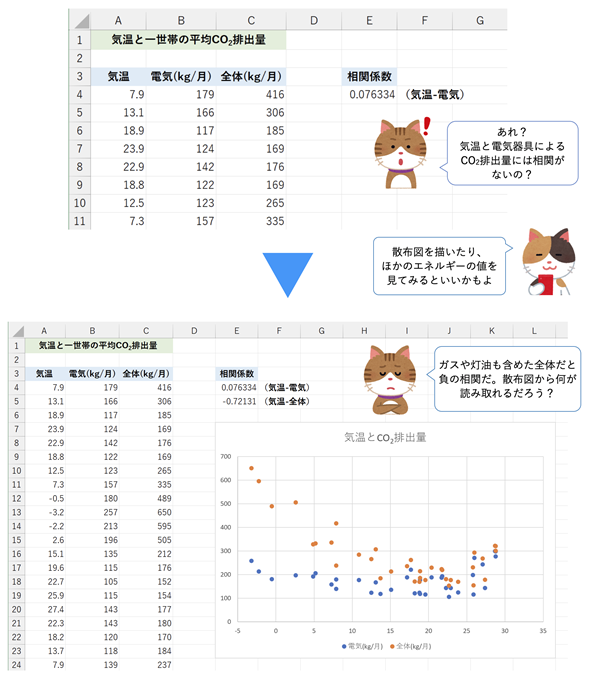
図1 気温とCO2排出量の関係を調べる
相関係数が1に近ければ正の相関(一方が増えれば他方も増える)、-1に近ければ負の相関(一方が増えれば他方は減る)となるが、気温と電気器具によるCO2排出量の相関係数は0に近い(無相関)。ということは、気温が上がっても下がっても、電気器具によるCO2排出量は変わらないということなのだろうか。個人的には夏の電気代が高いので直感に反するのだが……。
北海道、関東甲信といってもかなり広いので、気温を札幌と東京で代表させるのはやや無理がありますが、図1を見ると気温と電気によるCO2の排出量の相関係数は0に近いので、相関はないようです。暑い時期にはエアコンがフル稼働し、夏の電力不足が毎年のように話題になるので、気温が上がればCO2の排出量も増えるような気がしますが、どうもそうではないように見えます。
一方、ガスや灯油なども含めると、相関係数が-1に近い値になるので、負の相関が見られます。つまり、気温が下がるほどCO2の排出量が増えるというわけです。
なぜ、このような結果になるのかを考えていきたいと思います。……が、その前に、そもそも相関係数とはどのような計算で求められる値なのか、どういう意味を持つのかをきちんと確認しておきましょう。今回はそこからスタートです。
この記事は、データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第13回です。第3回〜第6回は代表値や散布度について、データ可視化入門【特別予告編】の後、第7回〜第12回は可視化をテーマに解説してきました。今回から第15回までは「関係」に注目し、相関係数や回帰分析などについて見ていきます。トップページから全体の目次が参照できます。また、次回を見逃さないために記事冒頭のボタンからぜひメール通知にご登録ください。
この記事で学べること
今回は以下のようなポイントについて、分析の方法や目の付け所を見ていきます。
- 相関係数の求め方と意味 …… 相関係数の計算方法を図形的に見ながら意味を理解する
- 相関係数の落とし穴(1) …… 相関係数が小さくても関係が強いこともある
- 相関係数の落とし穴(2) …… 疑似相関(見た目の相関)にご注意
- 相関係数の落とし穴(3) …… 相関関係は因果関係ではない
では、基本の基本である相関係数の計算方法から見ていきます。サンプルファイルの利用についての説明の後、本編に進みましょう。
サンプルファイルの利用について
本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントで使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントで使える無料のGoogleスプレッドシート(Google Sheets)をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、ファイルを共有して参照できるようにします。リンクを開き、メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
相関係数の基本をざっとおさらい
相関係数についてはこの連載の中で既に少し触れていますし、初歩の初歩なのでご存じの方も多いかと思いますが、理解を確実にするために、おさらいから始めましょう。相関係数は2つの変数にどの程度直線的な関係があるかを表す値です(図2)。
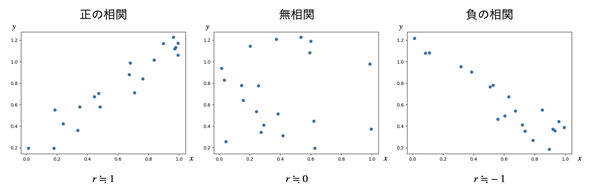
図2 相関係数と変数同士の関係の強さ
相関係数はrという文字で表されることも多い。rが1に近い場合は、図の左側のように、変数xの値が増えればそれに対する変数yの値も増える(正の相関)、逆に、rが-1に近い場合は、図の右側のように、変数xの値が増えればそれに対する変数yの値は減る。rが0に近い場合は、図の中央のように、変数xの値の大小と変数yには直線的な関係はない(無相関)。
明確な基準はありませんが、一般に、相関係数rの値は以下のように評価されます。
- 0 ≤ |r| ≤ 0.2 …… ほぼ相関はない
- 0.2 < |r| ≤ 0.4 …… 弱い相関がある
- 0.4 < |r| ≤ 0.7 …… 相関がある
- 0.7 < |r| ≤ 1 …… 強い相関がある
相関係数はあくまでも変数同士の直線的な関係の強さを表すので、相関係数が0に近くても(直線的ではないが)何らかの関係があることもあります。また、複数のグループが混在している場合、それぞれのグループに分けると相関関係が見られることもあります。図2の中央の図も、yの値が1.0以上のグループと1.0未満のグループのデータが混在しているのかもしれません。yの値が小さいグループには負の相関がありそうに見えますね。このことについては、また後述することにします。
相関係数の値が1あるいは-1に近い場合は、「直線的な関係がある」と言えますが、直線の傾きを表すものではありません。相関係数はあくまで関係の強弱を表すもので、変数同士がどれだけ「同じ方向に動く」かということを表します(次の項で説明する相関係数の図形的な意味を見ればよく分かります)。
では、相関係数を求めてみましょう。相関係数を求めるには、ExcelのCORREL関数*1が使えます。
*1 この連載では、通常、記事の末尾にある「関数リファレンス」セクションでExcel関数の書式を詳しく紹介しています。しかし、今回の記事で扱うExcel関数は、全て過去の記事で解説しているため、「関数リファレンス」セクションは掲載しません。今回取り上げる各Excel関数の書式については、初出時の関数に設定しているリンク先(ジャンプ先は過去記事の「関数リファレンス」)を参照してください。
CORREL関数についても、既にご存じの方も多いと思います。簡単な例(架空の事例)を使って関数の使い方を確認しておきましょう(図3)。サンプルファイル(13a.xlsx)をこちらからダウンロードし、[相関係数を求める]ワークシートを開いて取り組んでみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
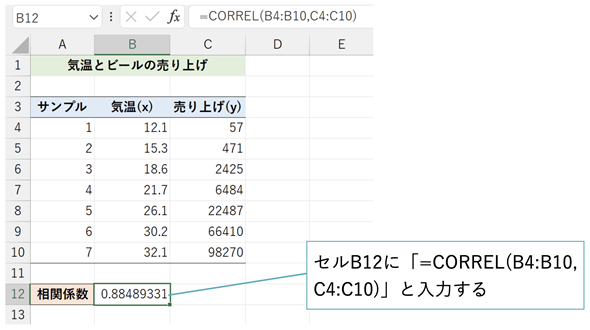
図3 CORREL関数を使って相関係数を求める
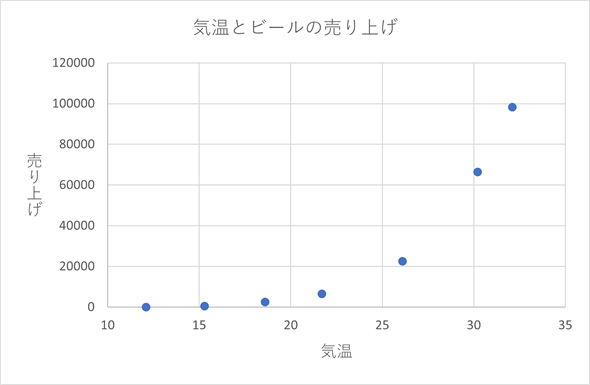
CORREL関数には変数xの範囲と、それに対する変数yの範囲を指定すればよい。具体的には=CORREL(B4:B10,C4:C10)と入力すればよい。この例では、0.88...という値が求められ、強い正の相関があることが分かる。つまり、気温が上がればビールの売り上げも上がるということになる。
実は、図3の例はさらに分析の余地があるのですが、それについては後述することにします。
実際には、ビールの売り上げはこのデータのように極端ではありません。夏場がピークであることは確かですが、春先から徐々に増えていきます。また、気温の上がる時期だけでなく、12月にも売り上げが多いようです(アサヒグループホールディングスのファクトブックなどによる)。
相関係数の計算方法を図形的に見てみよう 〜 相関係数の意味がよく分かる!
CORREL関数が入力できれば、相関係数は簡単に求められます。しかし、完全に「ブラックボックス」ですね。いったいどういう根拠で、どういう計算が行われているのかが全く分かりません。実用上、苦労することはないかもしれませんが、やはり理屈を理解した上で使いたいものです。
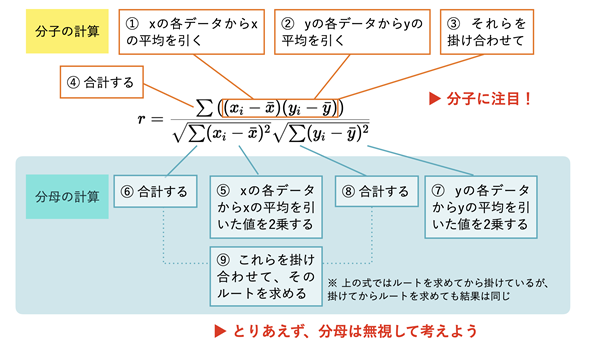
そこで、相関係数の意味を図形的に理解できるようにしてみましょう。まず、相関係数の定義を掲載します。数式が登場するので、数式の苦手な方はちょっと腰が引けてしまうかもしれませんが、ご心配なく。単純な四則演算レベルの計算しか出てきませんし、重要なのは分子だけです。なお、以下の解説と定義通りに計算する方法については動画も用意してあります。相関係数の図形的な意味と計算方法を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。
動画1 相関係数の定義と計算方法
(1)式の意味と計算の手順は図4のようにまとめられます。分子と分母に分けて説明していますが、図形的に理解する上では、分母は完全に無視してもらって構いません(分母は相関係数の値が-1〜1の範囲になるように調整しているだけです)。
分子の計算では各データの値から平均値を引いています。これは、原点(0, 0)を平均値の位置に移動しているのと同じことです。つまり、平均値が原点(0, 0)になります。そして、それらの積(xi−x̄)(yi−ȳ)を求めています。その計算を図として表し、意味を考えてみましょう(図5)。
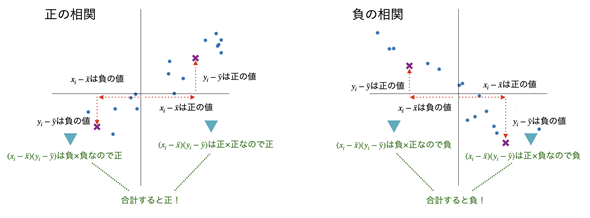
図5 相関係数の図形的な意味
正の相関の例では平均値が原点になるので、原点を通るような右肩上がりのグラフになる。このとき、右上の×点のX軸の値とY軸の値を乗算すると、正×正なので正の値になる。左下の×点は、負×負なのでやはり正の値になる。それらを全て合計すれば正の値になる。
負の相関の例では同様に原点を通るような右肩下がりのグラフになる。このとき、右下の×点のX軸の値とY軸の値を乗算すると、正×負なので負の値になる。左上の×点は負×正なのでやはり負の値になる。それらを全て合計すれば負の値になる。
なお、無相関の場合は、正と負が相殺されて0に近い値になる。
図5からも分かるように、
の値が正になる場合が正の相関、負になる場合が負の相関です。
いかがでしょう。そういうことだったのか、と納得していただけたでしょうか。
相関係数を定義通りに計算してみよう
図4で見た(1)式の意味と計算の手順に合わせて数式を入力すれば、相関係数の計算ができそうですね。実際にやってみましょう。……といっても、相関係数の意味が十分に理解できていれば、CORREL関数を使えばいいので、ここからの計算は絶対に必要というわけではありません。先を急ぐ方は、次の項「相関係数の落とし穴(1)」に進んでいただいてけっこうです。
図6は完成例です。上で見たサンプルファイルの[相関係数の計算]ワークシートを開き、表1(図6の後に掲載しています)に従って数式を入力していきましょう。Googleスプレッドシートの例については後述します。
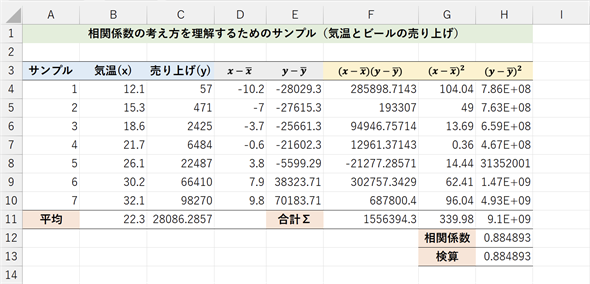
図6 相関係数を定義通りに求めてみる
(1)式の定義に従って計算してみた例。入力すべき数式や関数は以下の箇条書きと表1にまとめてあるので、サンプルファイルに入力して計算の手順を確認しておくとよい。「ブラックボックス」の中身(相関係数の意味と計算の方法)が理解できていれば、いちいち手順通りに計算しなくても、CORREL関数を使えばよい。
各セルに入力されている数式や関数をコピーしやすいように箇条書きで示しておきます。なお、従来のExcel(2019以前のバージョン)で=B4:B10-B11のような配列数式を入力するには、入力したい範囲のセルを選択した状態で先頭のセルに配列数式を入力し、入力終了時に[Ctrl]+[Shift]+[Enter]キーを押す必要があります。
- セルB11: =AVERAGE(B4:B10)
- セルC11: =AVERAGE(C4:C10)
- セルD4: =B4:B10-B11
- セルE4: =C4:C10-C11
- セルF4: =D4:D10*E4:E10
- セルF11: =SUM(F4:F10)
- セルG4: =D4:D10^2
- セルG11: =SUM(G4:G10)
- セルH4: =E4:E10^2
- セルH11: =SUM(H4:H10)
- セルH12: =F11/SQRT(G11*H11)
- セルH13: =CORREL(B4:B10,C4:C10)
表1では上記の内容を一覧としてまとめ、数式の意味や計算結果を「備考」に記しています。
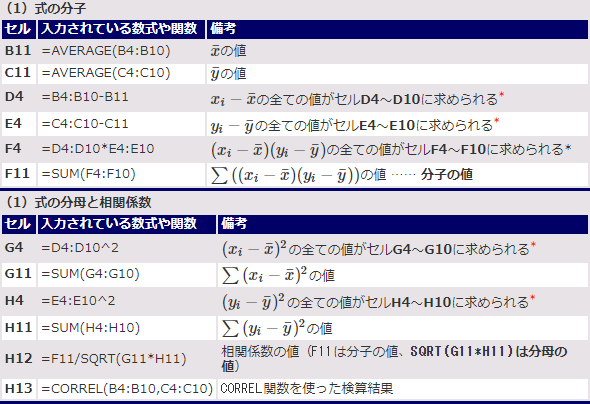
表1 図6で入力した数式や関数の一覧
この表の通りに入力していけば、(1)式での計算方法が理解できる。Googleスプレッドシートでは、*で示した箇所の数式は、ARRAYFORMULA関数の引数に指定する必要がある(後述)。
上の例ではスピル機能を使って複数の計算を一度に行っていますが、Excelのスピル機能を使わずに計算した例もサンプルファイルの[相関係数の計算(スピルを使わない)]ワークシートに含めてあります。その場合、例えば
を求めるのであれば、セルD4に=B4-$B$11と入力し、セルD4をセルD10までコピーします。サンプルファイルで確認してみてください。
Googleスプレッドシートでは、Excelのスピル機能や配列数式に相当する機能がARRAYFORMULAという関数で提供されています。例えば、セルD4に入力する数式であれば=B4:B10-B11の代わりに=ARRAYFORMULA(B4:B10-B11)と入力します。詳細については、こちらのサンプルファイルを開き、メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてご参照ください。
相関係数の落とし穴(1) 〜 相関係数が0に近くても関係が強いこともある
冒頭で紹介した気温とCO2排出量の例を思い出してください。図1の下の部分を再掲します。気温と電気によるCO2の排出量については、相関はないようです。一方、ガスや灯油なども含めると、負の相関が見られます。つまり、気温に関わらず電気によるCO2排出量は変わらず、全体で見ると気温が下がるほどCO2の排出量が増えるというわけです。夏や冬には電気の消費量が増えそうなので、この結果は直感に反しますね。
サンプルファイル(13b.xlsx)はこちらからダウンロードできます。[気温とCO2排出量 (散布図付き)]ワークシートを開くと図7の内容が確認できます。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。なお、散布図の作成方法についてはここでは触れません。前回の「散布図を徹底活用して「関係」を可視化 〜 関係と規模を一度に見る」をご参照ください。
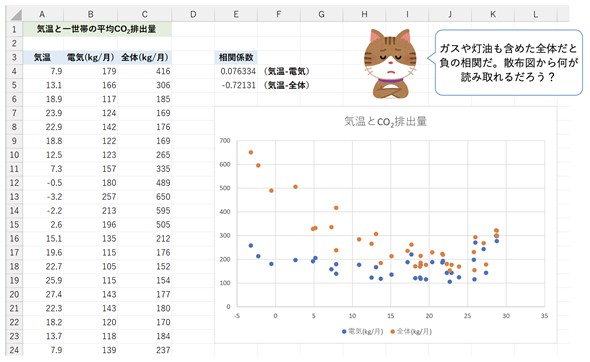
図7 気温とCO2排出量の関係
セルE4には=CORREL(A4:A39,B4:B39)が入力されており、セルE5には=CORREL(A4:A39,C4:C39)が入力されている。気温と電気によるCO2排出量の相関係数は0に近い。つまり直線的な関係はない(無相関)。しかし、気温と(灯油やガスも含めた)全体のエネルギーによるCO2排出量の相関係数は-1に近い(負の相関)。これはどういうことを表しているのだろうか。
まず、全体のCO2排出量について考えてみましょう。これは簡単です。気温があまりに低いと電気での暖房が追いつかないからです。その場合は灯油などの消費が多くなるので、全体のCO2排出量が多いというわけです。気温が高いとき(図の右側)は気温とCO2排出量はやや比例しているようですが、エアコンがフル稼働し、灯油などは使われないので、電気によるCO2排出量と全体のCO2排出量にはさほど差がありません。
次に、気温と電気によるCO2排出量の関係です。相関係数を見ると「関係がない」と言えそうですが、実際のところ、夏と冬にはエアコンも使われるので、春や秋よりもCO2排出量が多くなりそうです。確かに、直線的な関係ではありませんが、実はU字形のグラフが描けるような関係になっています。そこで、サンプルファイルの[気温とCO2排出量 (電気のみ)]ワークシートを開き、気温と電気だけの散布図を見てみましょう(図8)。
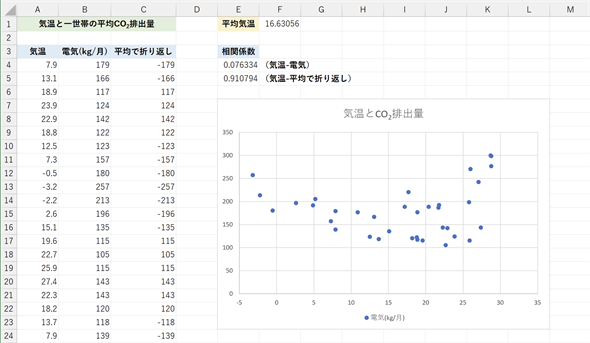
図8 気温と電気によるCO2排出量の関係
図7では、全体のCO2排出量が多かったので、電気のCO2排出量があまり目立たなかったが、U字形の分布になっているように見える。「平均で折り返し」という項目については以下で解説する。
どうやら、気温と電気によるCO2排出量は直線的な関係ではなくU字形の関係があるようです。そこで、ちょっと乱暴ですが、気温が平均よりも低い場合には、CO2排出量にマイナスを付けてみましょう。そうすれば、気温の平均の位置で値が折り返され、U字形が直線に近くなるはずです。
セルC4には、=IF(A4:A39<F1,-B4:B39,B4:B39)という式が入力されています。スピル機能を使わないのであれば、セルC4に=IF(A4<$F$1, -B4, B4)と入力し、セルC39までコピーすれば同じ結果になります。Googleスプレッドシートの場合は、=ARRAYFORMULA(IF(A4:A39<F1,-B4:B39,B4:B39))と入力します。
相関係数は、図7で見たのと同じ式で求められます。セルE5の値は0.91...とかなり1に近い値です。つまり、正の相関になります。気温が低いときと高いときに電気によるCO2排出量が大きくなるという直感は間違っていなかったようです。
なお、図3で見た気温とビールの売り上げについても「1に近い値が求められたので正の相関がある」と安心してしまわずに散布図を描くようにしましょう。直線的ではない関係があるかもしれないからです。散布図は図9のようになります。こちらは、最初に利用したサンプルファイル(13a.xlsx)の[気温とビールの売り上げ]ワークシートに含まれています。
図9から、気温とビールの売り上げには指数関数的な関係がありそうだということが分かります。ということは、対数を取れば直線的な関係になるはずです。そこで、売り上げの対数を取った値を基に散布図を作成し、さらに相関係数も求めてみます。サンプルファイル(13a.xlsx)の[気温とビールの売り上げ(対数)]を開くと、図10のような画面が表示されます。
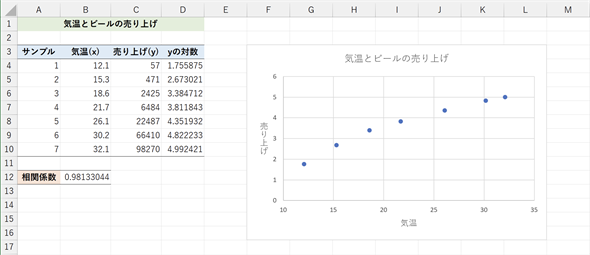
図10 気温とビールの売り上げの対数
散布図を描くと、やや弓なりになっているが、図9に比べると直線的であることが分かる。セルD4には=LOG(C4:C10)が入力されており、売り上げの対数が求められている(底は10)。セルB12には=CORREL(B4:B10,D4:D10)と入力されており、気温と売り上げの対数の相関係数が求められている。元の値で求めたときよりも、さらに1に近い値になっていることが分かる。
気温とビールの売り上げのデータは、あえてこのような結果になるように作成した架空のデータですが、表面的な数値だけに頼らず、データをさまざまな角度から見ることの大切さはご理解いただけたと思います。
相関係数の落とし穴(2) 〜 疑似相関にご注意
相関係数に関連する落とし穴の一つとして、疑似相関がよく知られています。架空の話ですが、ビールの売り上げと水難事故に正の相関が見られたとします。ビールが売れると水難事故が起こるのでしょうか。これは見た目の相関(疑似相関)です。
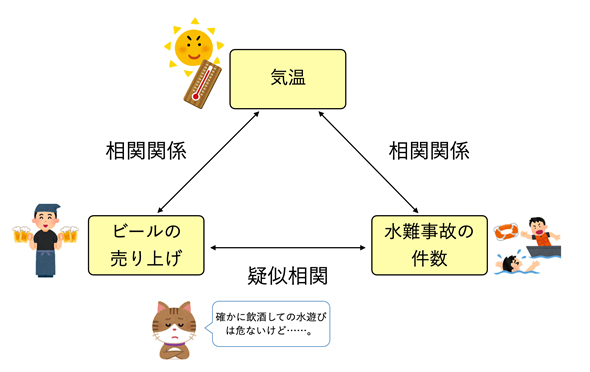
ビールが売れるのは一般に夏場の暑い時期です。その時期には海や川で水遊びする人が多いので水難事故が多くなるのは当然と言えば当然です。真相は、気温とビールの売り上げ、気温と水難事故に相関があるという話だったわけです(図11)。
また、単なる偶然やデータ数の少なさが原因ということもあります。ニコラス・ケイジの映画出演数とプールで溺死する人の数に正の相関があるといった例などが有名です。
相関係数の落とし穴(3) 〜 相関関係は必ずしも因果関係ではない
相関係数のもう一つの落とし穴は、相関関係を因果関係(=原因と結果の関係)と誤解してしまうことです。
気温とビールの売り上げについては、因果関係と考えてもよさそうですが、そうではない(むしろ因果関係ではない)場合もよくあります。気温が上がる(原因)とビールが売れる(結果)ことはあるでしょうが、ビールが売れる(原因)と気温が上がる(結果)というのは現実的ではないので、気温とビールの売り上げについては、因果関係の可能性があると解釈してもよさそうです。
上でも触れましたが、実際にはビールの売り上げは12月にも上がります(おそらく忘年会シーズンのため)。気温はビールの売り上げが上がる原因の一つですが、唯一無二の原因でもありません。他の要因があることも考慮する必要があります。
しかし、相関係数が高くても「因果関係の可能性を示唆する」とは解釈できない事例も数多くあります。例えば、ゲームに費やす時間と成績に負の相関がある場合、ゲームにのめり込んでしまうから勉強をしなくなるのか、勉強するのが嫌だからゲームに逃避しているのかは分かりません(図12)。安易に因果関係と見なすのは危険です。やはり背景を調べることが重要です。
図12 相関関係は必ずしも因果関係ではない
人は2つの出来事が同時に起こると因果関係だと思う傾向(認知バイアス)があるので、相関関係は因果関係と混同されやすい。しかし、相関関係は必ずしも因果関係ではないことに注意。
発展:順序尺度や名義尺度で、関係を表す数値を求めるには
分布に偏りがある場合には、間隔尺度のデータでも、元の値ではなく順位を使って代表値(中央値)や散布度(四分位範囲)を求めることがあります。相関係数についても同様に、元の値ではなく順位を使って求めた「順位相関」の方が適切です。また、元のデータが順位を表す値である場合(順序尺度の場合)にも順位相関を使います。
一方、名義尺度の場合はクラメールの連関係数などを使います。
以降の例については、作成例をこちら(13c.xlsx)に用意してあるので、解説と併せてご参照ください。Googleスプレッドシートのサンプルはこちらです。
これまでに見てきた相関係数はピアソンの積率相関と呼ばれるもので、間隔尺度のデータに対して使われるものです。
スピアマンの順位相関
順位相関にはスピアマンの順位相関やケンドールの順位相関がありますが、ここではスピアマンの順位相関を紹介します。スピアマンの順位相関rsは以下の式で表されます。
といっても、実はこの式で計算しなくても、順位を表す値をCORREL関数に指定すれば、同じ値が求められます。なお、同じ順位がある場合には、順位をRANK.AVG関数で求めてCORREL関数で相関係数を求めます。[順位相関を求める(同順位がある場合)]ワークシートを開くと図13の表が参照できます。なお、以下の操作と、次項のクラメールの連関係数を求める操作については動画も用意してあります。数式を入力する手順を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。
動画2 「スピアマンの順位相関」と「クラメールの連関係数」の計算方法
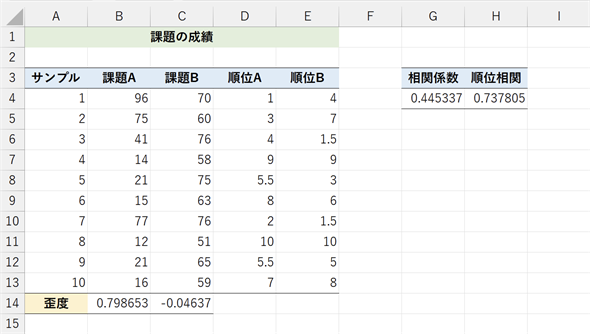
図13 順位相関を求める
10人に課題Aと課題Bを与えたときの成績(架空データ)。歪度(わいど)を見ると課題Aの成績は小さい値が多いことが分かる。分布に歪みがあるので、順位相関を使うとよい。元のデータで求めた相関係数の値は比較的小さいが、順位相関の値はかなり大きい。歪度については本連載の第4回「分散/標準偏差 〜 給与の格差ってどれぐらい?」のコラム「歪度と尖度で分布の形を知る」も参照のこと。
各セルに入力されている関数は以下の通りです。
| セル | 入力されている数式 | 備考 |
|---|---|---|
| B14 | =SKEW(B4:B13) | 課題Aの歪度 |
| C14 | =SKEW(C4:C13) | 課題Bの歪度 |
| D4 | =RANK.AVG(B4:B13,B4:B13,0) | 課題Aの順位(同順位は順位の平均) |
| E4 | =RANK.AVG(C4:C13,C4:C13,0) | 課題Bの順位(同順位は順位の平均) |
| G4 | =CORREL(B4:B13,C4:C13) | 相関係数の値 |
| H4 | =CORREL(D4:D13,E4:E13) | 順位相関の値 |
スピル機能を使わない場合は、セルD4に=RANK.AVG(B4,$B$4:$B$13,0)を、セルE4に=RANK.AVG(C4,$C$4:$C$13,0)を入力し、セルD4とE4をセル13行目までコピーする。Googleスプレッドシートでは、セルD4に=ARRAYFORMULA(RANK.AVG(B4:B13,B4:B13,0))を、セルE4に=ARRAYFORMULA(RANK.AVG(C4:C13,C4:C13,0))と入力する。
クラメールの連関係数
名義尺度の変数同士の場合、クラメールの連関係数と呼ばれる値で関係の強さを求めることができます。連関係数は元のデータと、期待値(偏りがないと考えた場合の値)とのズレを表すような値です。ズレが大きいということは偏りがあるということです。連関係数はそれほど大きな値にならないので、一般に0.1以上であれば何らかの関係があると言われています。図14の例は[連関係数]ワークシートに含まれています。
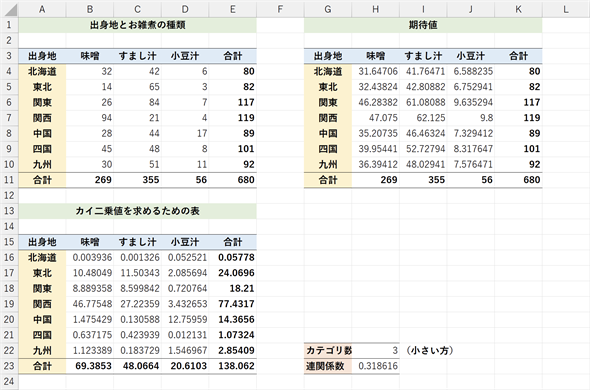
図14 クラメールの連関係数を求める
出身地と正月のお雑煮の種類についてアンケートを採ったデータ。農林水産省の「全国のいろいろな雑煮」を参考にして作成したものだが、値は架空のもの。沖縄ではお雑煮を食べる習慣があまりないとのことなので、データには含めていない。クラメールの連関係数は0.32程度なので、出身地と正月のお雑煮の種類には偏りがある(出身地によってお雑煮の種類は異なる)と言えそうである。
各セルに入力されている関数は以下の通りです。合計はSUM関数で求めていますが、簡単なので以下の表では省略しています。
| セル | 入力されている数式 | 備考 |
|---|---|---|
| H4 | =E4:E10*B11:D11/E11 | 期待値の全ての値がセルH4〜J10に求められる |
| B16 | =(B4:D10-H4:J10)^2/H4:J10 | 「(実測値と期待値のズレ)の2乗÷期待値」の全ての値がセルB15〜D20に求められる |
| H22 | =MIN(COUNTA(B3:D3),COUNTA(A4:A10)) | カテゴリ数の小さい方(お雑煮の種類=3) |
| H23 | =SQRT(E23/(E11*(H22-1))) | 連関係数の値 |
スピル機能を使わない場合は、セルH4に=$E4*B$11/$E$11を入力し、セルJ10までコピーする。セルB16には=(B4-H4)^2/H4を入力し、セルD22までコピーする。Googleスプレッドシートでは、セルH4に=ARRAYFORMULA(E4:E10*B11:D11/E11)を、セルB16に=ARRAYFORMULA((B4:D10-H4:J10)^2/H4:J10)と入力する。
期待値とは、2つの変数に関係がないと考えられるときの値です。つまり、出身地とは関係なく、お雑煮の種類は一定の割合で、偏りがないと考えられるときの値です。セルB11〜E11を見れば、全体では、味噌、すまし汁、小豆汁が、それぞれ269/680、355/680、56/680の割合になっていることが分かります。北海道出身者の数はセルE4の80人なので、一定の割合であるとすれば、北海道の味噌は80×269÷680になるはずです。セルアドレスを使った数式で表すなら=E4*B11/E11となります。同様に北海道のすまし汁は=E4*C11/E11、小豆汁は=E4*D11/E11で期待値が求められます。変化する部分を範囲として表せば、=E4:E10*B11:D11/E11という数式で全ての期待値が求められるわけです。
セルB16〜D22に入力されている数式=(B4:D10-H4:J10)^2/H4:J10は、実測値(セルB4〜D10)と期待値(セルH4〜J10)の差を二乗し、それが期待値に対してどれぐらいの割合であるかを求めたものです。つまり、期待値に対するズレの程度を表します。セルE23はそれらの合計です。これがカイ二乗値と呼ばれる値です。つまり、カイ二乗値は以下のように表されます。
連関係数Vは以下の式で求められます。nはデータの個数、kはカテゴリ数の小さい方です。
カイ二乗値は独立性の検定と呼ばれる統計的検定を行うための基本です。独立性の検定では、カイ二乗値を基に、カイ二乗分布の右側確率を求めます……が、それについては、この連載の続編である推測統計編で取り扱うことになります(ただ、かなり先になりそうですが)。
今回は、相関係数を求めて変数同士の直線的な関係の強さを評価する方法を紹介しました。直線的な関係がなく、相関係数が0に近くても、何らかの関係がある場合も考えられます。また、疑似相関に注意することや、相関関係が必ずしも因果関係ではないことについても触れました。さらに、発展的な内容として順序尺度や名義尺度の場合に関係の強さを求める方法についても紹介しました。
次回は、単回帰分析による予測の方法を見ていきます。どうぞお楽しみに!
Copyright© Digital Advantage Corp. All Rights Reserved.