チェビシェフ距離(Chebyshev distance)/L∞ノルムとは?:AI・機械学習の用語辞典
用語「チェビシェフ距離」について説明。2点間の距離を計測する方法の一つで、2つの点座標(n次元)で「次元ごとの距離(=各成分の差)の絶対値」のうち「最大値」を距離として採用する計算方法を意味する。
用語解説
数学/統計学/機械学習におけるチェビシェフ距離(Chebyshev distance、Chessboard distance:チェス盤距離)とは、2点間の距離を計測する際に、n次元ベクトルで表現されるそれらの点座標の次元ごとに距離(=成分間の差)の絶対値を求めて、その中の最大値を距離とする方法である。
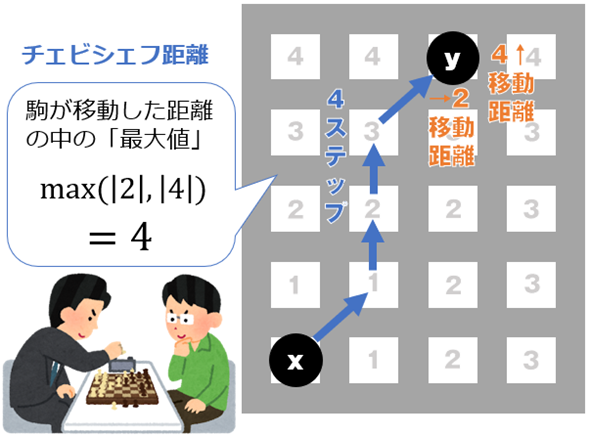
チェビシェフ距離は、n次元のチェス盤の上をキング(駒)が移動する手数(=ステップ数)によく例えられる(図1)。キングは斜めにも真っ直ぐにも動けるため、例えば左下にあるx地点から右上にあるy地点に最短距離で移動する場合、その移動のステップ数がそのまま2点間のチェビシェフ距離となる。
図1のように、チェス盤の上で点座標xが(0,0)から点座標yが(2,4)に駒(キング)を最短距離で移動させる場合、4マス移動するので、チェビシェフ距離は4になる。
このチェビシェフ距離d∞(x,y)は、次のように数学的に計算できる(計算式については後述する)。
「チェビシェフ距離」の定義と数式
点xから点yのチェビシェフ距離を求める数式は、以下のように定義できる。
この数式では、2つのn次元ベクトルで各成分の差の絶対値を取り、その中の最大値を「距離」として採用している。このためチェビシェフ距離は、「最大距離(Maximum metric)」や「max距離」とも呼ばれる。
||……||という数学記号は、ベクトル空間における「長さ/距離」を表現する概念であるノルム(norm)を意味する。チェビシェフ距離は、L∞ノルムや無限大ノルムとも呼ばれる。ちなみにL∞ノルムは、NumPyライブラリのnp.linalg.norm(<x-y点間距離の多次元配列データ>, ord=np.inf)関数で計算できる。
マンハッタン距離やユークリッド距離との違い
チェビシェフ距離は、マンハッタン距離やユークリッド距離と同様に、2点間の距離を計算するための手法の一つである。それぞれどう違うかを、以下に箇条書きで簡単にまとめておく。
- マンハッタン距離(L1ノルム): 2点間の座標差(絶対値)を合計。例えば機械学習のL1正則化(ラッソ回帰)で使われている。
- ユークリッド距離(L2ノルム): 2点間の「直線距離」を算出。最も一般的な距離の計算方法。例えば機械学習のL2正則化(リッジ回帰)で使われている。
- チェビシェフ距離(L∞ノルム): 2点間の座標差(絶対値)のうち最大値を算出。2つのn次元ベクトルで各成分の差がほとんど同じだが、そのうちの1つでも大きく差があれば、それを高く評価したい場合に使える。ただし、このような目的は「機械学習」の分野ではあまり多くないと考えられるため、実際の利用機会は限られるだろう。
Copyright© Digital Advantage Corp. All Rights Reserved.