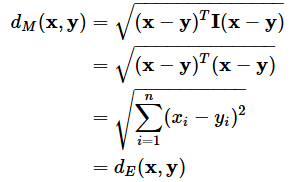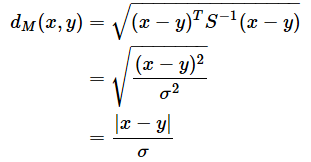マハラノビス距離(Mahalanobis distance)とは?:AI・機械学習の用語辞典
用語「マハラノビス距離」について説明。2点間の距離を計測する方法の一つで、「“普通の距離”(=ユークリッド距離)を一般化したもの」とも言われる。データの分布(共分散行列)を考慮することで、データのばらつき具合や相関関係を反映した距離を計算できる。異常値や外れ値を識別するために有効であり、特に多次元データにおいて正確な距離測定が可能。
用語解説
数学/統計学/機械学習におけるマハラノビス距離(Mahalanobis distance)とは、n次元ベクトル(多変量空間)で表現される2点(例えばx=[x1,x2,...,xn]とy=[y1,y2,...,yn])間の「距離」を計算するための方法の一つである(具体的な計算方法は後述する)。マハラノビス距離は、“普通の距離”(厳密にはユークリッド距離、L2ノルム)の計算に「データの分布(厳密には共分散行列)」を加える。これにより、ユークリッド距離と違い、データのばらつき具合や相関関係が考慮されるようになるため、マハラノビス距離は「普通の距離を一般化したもの」とも言われる。
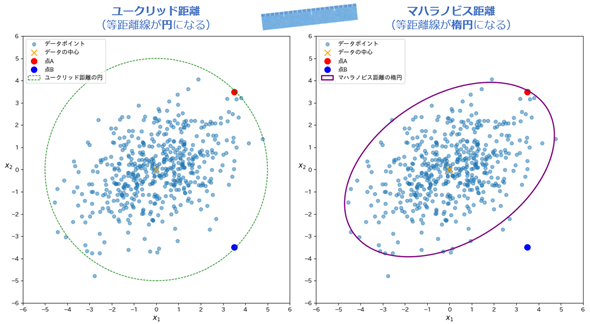
図1は、x1とx2という成分を持つ2次元ベクトルの架空のサンプルデータをプロットした例だ。左右のグラフ上には、データの中心(この場合は2次元座標系の原点)から等しい距離を結んだ線(=等距離線)をそれぞれ描画している。
左のグラフでは、「ユークリッド距離」を用いて計算している。この場合、等距離線は「完全な円」になる。この円の線上にある点Aと点Bは、データの中心からの距離が同じである。
右のグラフでは、「マハラノビス距離」を用いて計算している。この場合、データの分布や相関に基づいて、等距離線が「楕円(だえん)」になる。この楕円の線上にある点Aと、線上にない点Bは、異なる距離となっている。図を見ると分かるように、右側の青色の点Bは楕円から遠いため、データの中心からの距離は点Aよりも長い。
このように、距離にデータのばらつき具合や相関関係が考慮されると、他のデータ群から遠く離れた異常値はより長い距離として算出される。例えば、年齢と収入というスケールの異なるデータセットの場合、マハラノビス距離を用いることで、飛び抜けて収入の高い人は、ユークリッド距離よりも長い距離として判断できる。この方法により、データの異常値や外れ値をより正確に識別することが可能である。
「2点間のマハラノビス距離」の定義と数式
点xから点yのマハラノビス距離を求める数式は、以下のように定義できる。
数式の真ん中にあるSは共分散行列である。共分散行列(分散共分散行列とも呼ばれる)とは、多変量データの各変数(=各ベクトルの各成分)間の共分散をまとめた行列であり、つまりデータの分布を表す行列である。冒頭の説明の繰り返しになるが、マハラノビス距離では、計算に共分散行列を加えることで、データのばらつき具合や相関関係が考慮されるようになる。
多次元データに対する(不偏)共分散行列Sの数式は、データセットがn次元のベクトルz1, z2, ..., zmから成るm個のサンプルで構成されている場合、以下のように定義される(※標本データの場合は不偏共分散行列となるので分母をm−1にするが、母集団のデータの場合は分母はmにすること。ちなみに共分散行列を表す記号には、SだけでなくΣもよく使われる)。
この式を展開して計算すると、2次元ベクトルの場合は以下のような意味の行列が得られる。なお、以下のz:,1は、m個あるサンプル全体(:)での、n次元データの第1次元(=ベクトルの第1成分)を示すこととする(以下、同様の説明は省略する)。
3次元ベクトルの場合は、以下のような意味の行列が得られる。
ちなみに、共分散行列のSが単位行列Iの場合、マハラノビス距離は以下のようにユークリッド距離と同じ数式になる。
また、もしデータが多変量ではなく1変量(1次元ベクトル)の場合、マハラノビス距離は「2点間の直線距離を標準偏差で割る」という計算、つまり標準化するのと同じ計算になる。
ちなみにマハラノビス距離は、SciPyライブラリのscipy.spatial.distance.mahalanobis(<点xの1次元配列データ>, <点yの1次元配列データ>, <共分散行列Sの逆行列>)関数で計算できる。
「平均からのマハラノビス距離」の定義と数式
先ほどは2点間の距離を計算するための数式を示したが、マハラノビス距離はデータセット全体の平均からの距離を計算する数式もよく紹介される。ここでも式だけを簡単に示しておく。といっても、点yが平均μに変わっただけで、先ほどと同じ数式である。
この場合のマハラノビス距離は、点xがデータセットの中心(平均)からどれだけ離れているかを表す。
使い所と注意点
マハラノビス距離は、以下のような場面で活用できる。
- クラスタリング: 特徴量間の相関関係を考慮したクラスタリング手法での距離計算。
- 異常検知: データセット内の異常なデータポイントを検出するために使用。
- 判別分析: 多変量データにおけるグループ分けや分類問題における距離計算。
マハラノビス距離は、共分散行列を計算する必要があるため、データセットが十分なサンプル数を持つことが重要である。サンプル数が少ない場合、共分散行列の推定が不安定になる可能性があるので注意してほしい。
Copyright© Digital Advantage Corp. All Rights Reserved.