文字列の中から効率良くキーワードを探し出せ：コーディングに役立つ！ アルゴリズムの基本（7）（2/4 ページ）

プログラマたるものアルゴリズムとデータ構造は知っていて当然の知識です。しかし、教科書的な知識しか知らなくて、実践的なプログラミングに役立てることができるでしょうか（編集部）

[山下寛人，オイシックス株式会社]

KMP法

　力任せ法以外の方法は、普通にはなかなか思い付きません。しかし、より効率の良い方法がいくつもあります。

　文字列探索は、文字列の中の1文字と検索ワードの中の1文字にそれぞれ着目して比較することを繰り返します。ここで、着目している位置を指し示すものをポインタと呼ぶこととします。具体的には、何文字目かを表す数値の変数をイメージしてください。このポインタの進め方を工夫することで効率を良くすることができます。

　例えば、以下の例を考えてみましょう。

文字列：abababbbabc
検索ワード：ababc

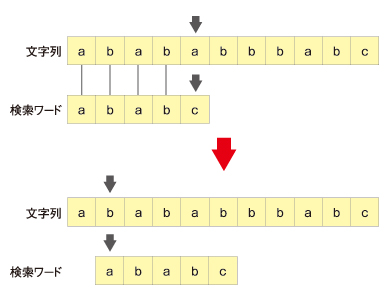
　力任せ法の場合を考えます。左から順に1文字ずつ比較すると「abab」まで一致しています。次の文字は、文字列では「a」、検索ワードでは「c」となり不一致です。そこで、文字列のポインタを1つ進めて2文字目の「b」、検索ワードの先頭「a」から比較を始めます。

　5文字目まで進んだ文字列側のポインタが、2文字目まで戻りました。これは実に無駄です。

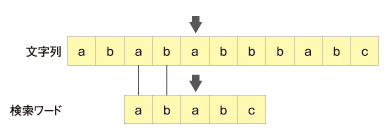
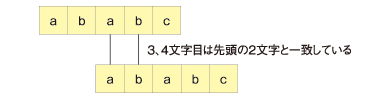
　「abab」まで一致していることが確かめられています。ということは3、4文字目の「ab」は、検索ワードの先頭の2文字「ab」と一致しており、文字列の5文字目と検索ワードの3文字目から比較を継続してもよいはずです。

　このように検索ワードのどの位置で不一致になったかを把握することによって、どこから比較を再開すればよいかをあらかじめ決めることができます。文字列側のポインタを戻さなくて済みます。

　この文字列探索アルゴリズムがKMP法です。KMPとは、このアルゴリズムを考えた人たち（Knuth-Morris-Pratt）の頭文字です。

KMP法の比較再開テーブル

　では、どこから比較を再開するかを、どのようにして考えればよいでしょうか。先ほどの例で考えてみましょう。文章だけでは分かりにくいので、ぜひ上のような図を書いてポインタの動きを追ってみてください。

　まず、1文字目の「a」で不一致になった場合。この場合は文字列のポインタを1つ進め、検索ワードのポインタは先頭にすればよいでしょう。

　2文字目の「b」で不一致になった場合。文字列のポインタはそのままに、検索ワードのポインタを先頭に戻せばよいでしょう。

　3文字目の「a」で不一致になった場合。先頭から再度比較するとしても、先頭も「a」なので必ず不一致になります。従って、文字列のポインタを1つ進め、検索ワードのポインタを先頭に戻します。

　4文字目の「b」で不一致になった場合。2文字目の「b」と同様に、文字列のポインタはそのままで、検索ワードのポインタを先頭に戻します。

　5文字目の「c」で不一致になった場合。先ほど見たように直前2文字の「ab」が一致するので、文字列のポインタはそのままに、検索ワードのポインタを3文字目にすればよいでしょう。

　このように、どこから比較を再開するかは、検索ワードの中に、検索ワードの先頭と同じ文字の並びがあるかどうかで決めることができます。5文字目の場合がもっとも分かりやすいでしょう。

　従って、比較再開テーブルは、検索ワード同士を比較して計算します。

KMP法の実装

　では、KMP法を実装しましょう。先ほどのプログラムの末尾にある「末尾1」というコメントに続けて、以下のプログラムを追加してください。

<script type="text/javascript">
String.prototype.getKMPNext = function() {
  var next = new Array();
 
  next[0] = -1;
  var n = next[0];
  for (var i = 0; i < this.length; i++) {
    while (n > -1) {
      if (this.charAt(i) == this.charAt(n)) { break; }
      n = next[n];
    }
    n++;
    var j = i+1;
    if (this.charAt(j) == this.charAt(n)) {
      next[j] = next[n];
    } else {
      next[j] = n;
    }
  }
 
  return next;
}
 
String.prototype.findKMP = function(str) {
  var next = str.getKMPNext();
 
  var text_idx_len = this.length - str.length + 1;
  var n = 0;
  for(var text_idx = 0; text_idx < text_idx_len; text_idx++) {
    while (n > -1) {
      if (this.charAt(text_idx) == str.charAt(n)) { break; }
      n = next[n];
    }
    n++;
    if(str.length <= n) {
      return text_idx - str.length + 1;
    }
  }
  return null;
}
 
function findTextAreaKMP(text_id, search_id) {
  var text = getStringById(text_id);
  var search = getStringById(search_id);
  alert(text.findKMP(search));
}
</script>
<input type="button" onClick="findTextAreaKMP('area1','search');" value="findKMP">
<!-- 末尾2 -->

　プログラムを解説します。

2〜22行目

比較再開テーブルを作成する関数です。

配列nextが、検索ワードの何文字目で不一致になったときに、何文字目から比較再開するかを保持します。例えば、2文字目で不一致だった場合は、next[1]に比較再開する文字の位置が入っています。next[i]=0だったら先頭になります。next[i]=-1だった場合は、文字列側のポインタを1つ進めて、検索ワード側のポインタを0にするという意味になります。

24〜40行目

KMP法で探索する関数です。

25行目

比較再開テーブルを計算します。

28行目

nが検索ワード側のポインタです。

29行目

text_idxが文字列側のポインタです。

30〜33行目

文字列の1文字と検索ワードの1文字を比較します。

一致するとnとtext_idxが両方1進みます。不一致になると比較再開テーブルを参照して、再度文字列と検索ワードの1文字を比較します。

比較再開テーブルに-1が入っていたらwhileループを抜けます。

35〜37行目

nが検索ワードの文字数まで進んだ＝全部一致したということで、一致した文字の位置を返します。