実践! 「MapReduceでテキストマイニング」徹底解説:テキストマイニングで始める実践Hadoop活用(2)(1/3 ページ)
Hadoopとは何かを解説し、実際にHadoopを使って大規模データを対象にしたテキストマイニングを行います。テキストマイニングを行うサンプルプログラムの作成を通じて、Hadoopの使い方や、どのように活用できるのかを解説します
「青空文庫」をテキストマイニング!
前回の「いまさら聞けないHadoopとテキストマイニング入門」では、Hadoopとテキストマイニングの概要や構成、MapReduceの仕組み、Hadoopの活用場面などを解説し、Hadoopの実行環境を構築しました。今回から、Hadoopを使い、テキストマイニングのMapReduceプログラムを作成していきます。
「青空文庫」というサイトをご存じでしょうか。青空文庫は、著作権が切れた日本の文学作品を掲載しているWebサイトで、青空文庫の全データをDVDや、BitTorrentによる配信で入手できます。今回は、このデータを使ってテキストマイニングを行いましょう。
前回、テキスト分類で、著者の性別、年齢、地域、職業などの属性も推定できると書きましたが、青空文庫は、他のデータにはない、著者属性があります。青空文庫の作品は、著作権が切れて、作者がなくなっている場合がほとんどで、著者の寿命が分かります。「著作権の消滅した作家名一覧」ページに作者の生年と没年月日一覧があるので、著者の寿命を抜き出せます。そこで、青空文庫の作品データから学習を行って、テキストデータから著者の寿命を推定するサンプルプログラムを作成していきましょう。
なお、遊び程度の精度しか出ないので、あくまで、テキストマイニングの手法を説明するためのサンプルプログラムとしてお考えください。
“重み”を推定する「回帰」とは
前回、bag-of-wordsでテキストをベクトル化する方法を説明しました。例えば、「男の中の男の中でも特に男臭い男は男の中の男の中の男となる」というテキストから名詞を抽出したベクトル「x」を考えます。
ベクトルは、以下のような2次元のベクトルで表されます。
(「男」の出現回数, 「中」の出現回数)
ここでは、以下のように表します。
x=(6,4)
このベクトル「x」のそれぞれの単語に対して“重み”を付けることを考えてみましょう。重みをベクトル「w」で表し、例えば、以下のような“重み”を付けることを考えてみます。
w=(5,3)
このxとwを掛け合わせると、以下のようになります。
y=wx=6×5+4×3=42
このyの値が寿命であれば、テキストに対して寿命が予測できることになります。wの値さえ分かれば、テキストに対して寿命が出力されるので、うまく寿命が予測できるような、この「w」の値を推定することが、目的となるわけです。
yの値を寿命のように連続値として考える問題を「回帰」、yが0より小さかったら男、大きかったら女などとカテゴリ分けする問題を「分類」といいます。
寿命を10代、20代、30代などにカテゴリに分けると、分類問題としても扱えるのですが、まずは、回帰問題として考えてみましょう。
「教師信号」と「損失関数」
青空文庫のデータを元にwを推定してみましょう。青空文庫の各作品をbag-of-wordsでベクトル化したものを、以下のように表します。
それぞれの作品の著者の寿命を、以下のように表します。
このような値を「教師信号」と言います。その名の通り、この値を教師として教えてもらいながら、wの値を推定するわけです。
では、どのように推定すればいいのでしょうか。以下の関数Lを考えてみます。
wxはxを重み付けして、寿命を予測する関数でしたが、この予測結果と、正しい結果である教師信号との誤差の二乗を考えます。
なぜ二乗をしているかというと、必ず正の誤差として出力されるようにするためです。このLを「損失関数」といい、寿命の予測値と正しい寿命の誤差が損失となります。この損失をなるべく小さくするようにwを推定すれば、正しい結果になるべく近い寿命が予測できるようになるわけです。
アルゴリズム「Widrow-Hoffの学習規則」とは
では、どのように損失がなるべく小さくなるようなwを求めればいいのでしょうか。青空文庫の作品xを1つずつ見ていって、損失が小さくなるようにwを更新していくアルゴリズムを考えます。このアルゴリズムを「Widrow-Hoffの学習規則」と言います。
以下のようにwを更新していきます。
は、
で、損失関数Lに
を代入したもの、
は刻み幅を表す正の定数です。
適当なw(例えば、ゼロベクトル)から始めて、xが与えられるたびに、
のwに関する微分を引いてwを更新していきます。
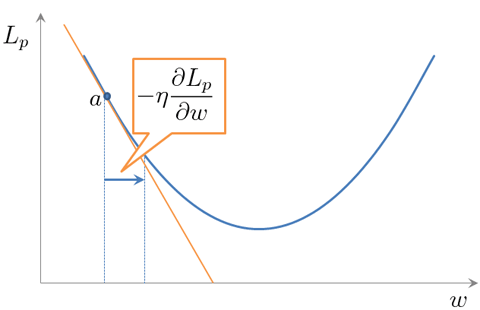
では、なぜこれを繰り返すことで、損失が小さくなっていくのでしょうか。以下にイメージを書きます。
はwの2次式ですので、2次曲線になります。
は、接線の傾きを表しています。点「a」における接線の傾きはマイナスなので、それとは逆のプラスの方向にwを更新すれば、
の極小値に近づきます。つまり、接線の傾きとは逆の方向にwを繰り返し移動していけば、最終的に損失の最小値に近づくというわけです。
この
を計算すると、以下の式になります。
つまり、青空文庫の作品xを1つずつ見ていって、寿命の予測値から正しい寿命を引いたものにxを掛けたものを重みベクトルから引いていくというプロセスを繰り返せばいいわけです。
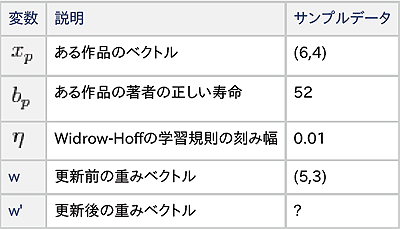
サンプルデータを使って重みを更新してみます。今まで出てきた変数の説明と、使うサンプルデータをまとめます。
w'を計算すると、以下の式で、重みベクトルは「(5.6,3.4)」に更新されます。
w'=(5,3)−0.01×(5×6+3×4-52)×(6,4) =(5,3)+0.1×(6,4) =(5.6,3.4)
次ページでは、青空文庫の作品をベクトル化するMapReduceプログラムについて解説します。
Copyright © ITmedia, Inc. All Rights Reserved.