第2回 ニューラルネットワーク最速入門 ― 仕組み理解×初実装(中編):TensorFlow 2+Keras(tf.keras)入門
ニューラルネットワーク(NN)の基礎の基礎。NNの基本単位であるニューロンはどのように機能し、Python+ライブラリでどのように実装すればよいのか。できるだけ簡潔に説明。また、活性化関数と正則化についても解説する。
前回は、ディープラーニングの大まかな流れを、下記の8つの工程で示した。
- (1)データ準備
- (2)問題種別
- (3)前処理
- (4)“手法” の選択: モデルの定義
- (5)“学習方法” の設計: モデルの生成
- (6)学習 : トレーニング
- (7)評価
- (8)テスト
このうち、(1)〜(3)のデータに関する処理内容は前回で説明済みである。そのデータを使って、今回は、(4)のニューラルネットワークのモデルの定義方法について説明する。それではさっそく説明に入ろう。※脚注や図、コードリストの番号は前回からの続き番号としている(前編・中編・後編は、切り離さず、ひとまとまりの記事として読んでほしいため連続性を持たせている)。
(4)“手法”の選択とモデルの定義: ニューロン
ニューラルネットワーク(=神経ネットワーク)とは、その名前の通り、脳の神経ネットワーク構造を模した機械学習の手法である。そのニューラルネットワークを理解するために、その基本単位であるニューロン(neuron:神経細胞)から話を始めたい。なおニューロンは、細胞体もしくは単位を意味するユニット(unit)や、ネットワーク構造における1つの結節点を意味するノード(node)などの名称でも呼ばれるので知っておいてほしい。
ニューロンの基本機能は、関数と同じように、複数の入力を受け取り、それらを使って何らかの計算をし、その結果を1つの出力として生成することだ。例として、2つの入力を受け付けるニューロンを考えてみよう。
Playgroundによる図解
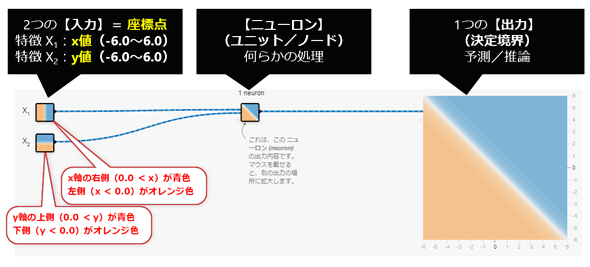
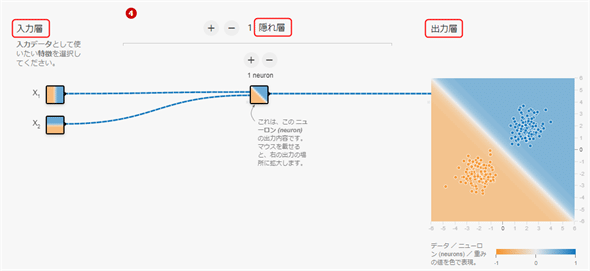
そのようなニューロンを、実際にPlayground上で作成したのが、図4-1だ(※右端にある大きな表示は、実際にはニューラルネットワークにおける「出力層」にある1つのニューロンだが、ここの説明においてはプレビュー確認用のグラフ領域と見なして、「出力層」であることは無視してほしい。また左端のΧ1/Χ2も、ニューロンではなく単なる入力だと見なしてほしい)。
なお座標が、(x, y)ではなく、(Χ1, Χ2) と表記されていることに注意してほしい。またΧ1/Χ2のような個々の入力値や個々のノードが表現するものは「特徴(feature)」(もしくは「特徴量」)と呼ばれ、例えばΧ1の場合、図4-1の左上にあるΧ1の四角を見ると、このデータは「右側(0.0 < x)が青色、左側(x < 0.0)がオレンジ色で、中央付近(x = 0.0)は白色」、言い換えると「決定境界の線が中央にまっすぐに縦に引かれている」という特性を持っている。
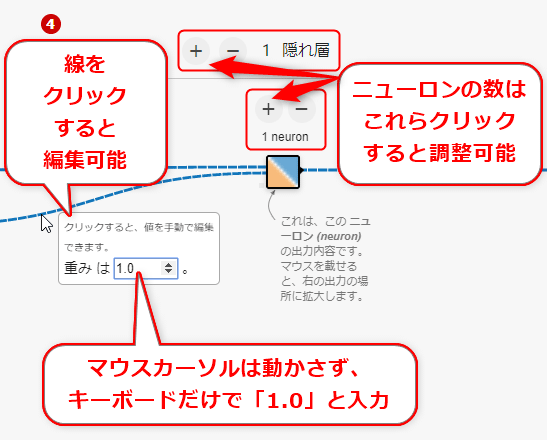
ちなみに、図4-1と同じ図を作成するには、こちらのリンク先のPlaygroundを開き、その中央の(4)で3つの線の上をそれぞれクリックし、それにより表示されるポップアップ上で[重み](後述)に「1.0」を入力する。入力方法のヒントを図4-2にまとめた。
入力
先ほど「重み」と出てきたが、重み(weight)とは入力を増幅〜減衰させるためのものである。先ほどは、座標 (Χ1, Χ2) (変数)のそれぞれに対して、1.0と固定値を指定したので、何も増減しないことになるが、本来はこの重みが学習によって自動的に計算されて決まるのである。重みはそれぞれw1、w2というパラメーターで置くとしよう。よって、ニューロンへの入力は次の式で表現できる。
ニューロンへの入力(未完成)=(w1 × Χ1)+(w2 × Χ2)
(未完成)と書いたが、実はこれで終わりではない。中学校で一次関数を学んだとき「切片(せっぺん)」という概念があったのを覚えているだろうか? 例えばy=ax+bという一次関数では、aが傾きで、bが切片である。bの値を0、1、2……と増やしていくと、一次関数のグラフに描かれた直線が、y軸の上方向に1ずつズレ上がっていくのがイメージできるだろうか? つまり切片があると、関数の位置をズラせるようになるのである。もし一次関数に切片がないと、常にグラフの原点(0, 0)を通るのみになって融通が利かない。
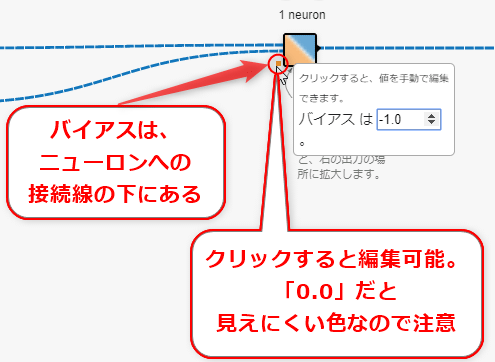
これと同じことが、上記のニューロンの式にもいえる。ニューロンで切片に該当するのがバイアス(bias)である。バイアスの数値を増減させたときのイメージを、図4-3に示す。背景がズレていく様子が見て取れるだろう。
ちなみに、Playgroundでバイアスを編集するには、ニューロンへの接続線の下にある小さな四角をクリックし、それにより表示されるポップアップ上で[バイアス]の数値を好きに入力するとよい。入力方法のヒントを図4-4にまとめた。数値が変わるたびに右側の大きなグラフがズレていくのが体験できるだろう。
バイアスをbというパラメーターで表現して加えると、ニューロンへの入力式は次のようになる。
ニューロンへの入力(完成)=(w1 × Χ1)+(w2 × Χ2)+b
何らかの計算結果の出力
前述したように、複数の入力を受け取ったニューロンは、それらの入力を使って何らかの計算をし、その結果を1つの出力として生成する。この「何らかの計算」は、活性化関数(Activation function)と呼ばれている。活性化関数とは、無制限の入力を、予測可能な範囲に変換するためのものである。
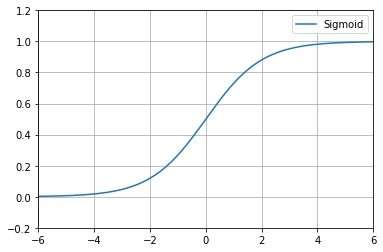
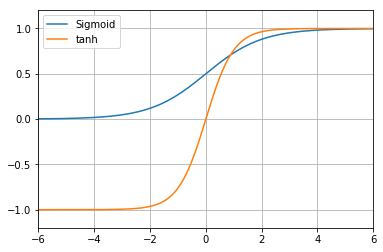
一般的な活性化関数の一つにシグモイド関数(Sigmoid function)がある。この関数は、どんな入力も、つまり−∞〜+∞の数値を、0.0〜1.0の範囲の数値に変換する。具体的には、図4-5のように変換する。なお、グラフの見方は、x軸が入力する数値で、y軸が変換後に出力する数値である。これを見ると、大きすぎる負の数は0に収束し、大きすぎる正の数は1に収束することが分かる。
ちなみに、Playgroundにおける最終的な出力は、-1.0(=オレンジ色)〜1.0(=青色)である。つまり、ニューラルネットワークの最後の最後にある活性化関数で、−1.0〜1.0の範囲の数値に変換しているのだ。この範囲に変換するのにちょうどよい活性化関数が、tanh関数(Hyperbolic tangent function)である。この関数は、図4-6のように変換する特性を持つ。
数値の範囲が最終的な出力の範囲と一致している方が、ニューロンの動きを把握しやすいと思うので、本稿ではシグモイド関数ではなく、tanh関数を使うことにする。
他にも活性化関数はあるが、それらについては後述のニューラルネットワークの部分で簡単に説明する。
さて、それではニューロンからの出力式を書き出してみよう。活性化関数をa()と置くと、次のようになる。
ニューロンからの出力=a((w1 × Χ1)+(w2 × Χ2)+b)
「ニューロンからの出力=活性化関数(ニューロンへの入力)」という式になっていることに気付けば難しくないだろう。参考までに計算してみよう。w1=0.6、w2=−0.2、b=0.8だと仮定して、座標(1.0、2.0)をニューロンに入力すると、
ニューロンからの出力=a((0.6 × 1.0)+(−0.2 × 2.0)+0.8)
=a(1.0)=0.761594...
と計算され、出力値は約0.76となる(※活性化関数自体の計算方法は割愛したので、上掲グラフにおけるtanh関数の曲線を見て、横軸1に対応する縦軸の値を目視確認してみてほしい)。
Pythonコードでの実装例
それでは、「ニューロン」の入力と出力を行うコードをPythonで記述してみよう。
TensorFlow 2.0のインストール
本稿では、TensorFlowのバージョン2系を必須とする(※Colabにインストール済みのTensorFlowバージョンが分からない場合は、import tensorflow as tf; print('TensorFlow', tf.__version__)を実行すれば、バージョンを確認できる)。
本稿が利用を前提とするColab(前編参照)にデフォルトでインストール済みのバージョンは、(2019年10月15日の執筆時点で)TensorFlow 1.15.0-rc3だった。このように、バージョンが2.xではない場合は、ライブラリ「TensorFlow」を最新版の2.xにアップグレードして使う必要がある。
そのためには、リスト4-0に示すいずれかのコードを実行して、アップグレード(もしくはインストール)する。実行後に、[RESTART RUNTIME]ボタンが表示されたら、クリックしてランタイムを再起動してほしい。ちなみに、そう遠くない将来、Colabではこのインストール手順を実行しなくても、最新のTensorFlow 2.xが利用できるようになるだろう。
# 最新バージョンにアップグレードする場合
!pip install --upgrade tensorflow
# バージョンを明示してアップグレードする場合
#!pip install --upgrade tensorflow===2.0.0
# 最新バージョンをインストールする場合
#!pip install tensorflow
# バージョンを明示してインストールする場合
#!pip install tensorflow===2.0.0
tensorflowパッケージのインポート
TensorFlowの利用環境が整ったとして話を進めよう。ここでは、ライブラリ「TensorFlow」のメインパッケージであるtensorflowをtfという別名でインポートし、その中で定義されているtf.kerasパッケージ(=TensorFlow同梱のKeras)を使って、モデル(=そのModelクラス*1のオブジェクト)を作成する。
*1 tf.kerasモジュール階層(=名前空間)のModelクラスとしてアクセスできるが、実際のクラス実装はtensorflow.python.keras.engine.trainingモジュール階層にあり、別名となっている。
Kerasにおけるモデルの書き方
Kerasによるモデルの作成方法/書き方は幾つかある。書き方は大きく分けて、
- Sequential(積層型)モデル: コンパクトで簡単な書き方
- Functional(関数型)API: 複雑なモデルも定義できる柔軟な書き方
- Subclassing(サブクラス型)モデル: 難易度は少し上がるが、フルカスタマイズが可能
の3種類がある。筆者のお勧めはFunctional APIかSubclassingモデル(Subclassing API)だが、今回は基本であるSequentialモデル(Sequential API)を使って書いてみよう(※説明をできるだけシンプルにするために、Functional APIやSubclassingモデルの書き方の説明は割愛する)。
さらにSequentialモデルにおいても、書き方は大きく分けて、
- Sequentialクラスのコンストラクター利用: 最も基本的でシンプルな書き方
- Sequentialオブジェクトのaddメソッドで追加: シンプルだが、より柔軟性のある書き方
の2種類がある。どちらを使うかは好みだが、取りあえずは基本である「コンストラクター(厳密には__init__関数)利用」の方を使って書いてみる(※「addメソッドで追加」の書き方についても割愛する)。
ここでは、2つの入力を受け付けて、それを使った計算結果を1つの出力として生成するニューロンを、モデル化(=モデル設計)する。
モデルの定義
モデル設計のコードを先に示してから、コード内容を説明する。おおよその内容は、コード内のコメントから理解できるだろう。
# ライブラリ「TensorFlow」のtensorflowパッケージを「tf」という別名でインポート
import tensorflow as tf
# ライブラリ「NumPy」のnumpyパッケージを「np」という別名でインポート
import numpy as np
# 定数(モデル定義時に必要となる数値)
INPUT_FEATURES = 2 # 入力(特徴)の数: 2
LAYER1_NEURONS = 1 # ニューロンの数: 1
# パラメーター(ニューロンへの入力で必要となるもの)
weight_array = np.array([[ 0.6 ],
[-0.2 ]]) # 重み
bias_array = np.array([ 0.8 ]) # バイアス
# 積層型のモデルの定義
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(
input_shape=(INPUT_FEATURES,), # 入力の形状
units=LAYER1_NEURONS, # ユニットの数
weights=[weight_array, bias_array], # 重みとバイアスの初期値
activation='tanh') # 活性化関数
])
# このモデルに、データを入力して、出力を得る(=予測:predictする)
X_data = np.array([[1.0, 2.0]]) # 入力する座標データ(1.0、2.0)
print(model.predict(X_data)) # 出力を得る
# [[0.7615942]] ……などと表示される
上から順に説明すると、ディープラーニング用のライブラリ「TensorFlow」と、多次元配列&数値演算用のライブラリ「Numpy」のインポート後に、
- 入力の数: INPUT_FEATURES = 2
- ニューロンの数: LAYER1_NEURONS = 1
を定数として定義している(※「出力の数」は1だが、ここでは使わないので定義していない)。
それらの定数を使ってモデル(リスト4-1ではmodelオブジェクト)を作成するわけだが、前述の通り(tf.keras.modelsモジュール階層の)Sequentialクラスのコンストラクターを利用している。このコンストラクターは、
__init__(
layers=None
)
と定義されており(※不要な引数は説明を割愛)、引数の意味は以下のとおりだ。
- 引数のlayers: レイヤー(層)をリスト値で指定する(※レイヤーは複数のニューロンで構成する層のこと、1層、2層、3層と増やせる。後述のニューラルネットワークで詳しく説明する)
今回はニューラルネットワークではなく、単一のニューロンを実装したいので、レイヤーも1つのみとなる。Kerasにおいてはさまざまな種類のレイヤーが用意されているが、今回は最も基本的な、
- Denseレイヤー: ニューラルネットワークで通常の全結合レイヤー
を使用する(※「全結合」(もしくは密結合)は文字通り「全て結合」という意味だが、今回はそれが「最も標準的なレイヤー間の接続方法」ということを押さえておけばよい)。Denseレイヤーのインスタンスをリスト化して、先ほどの引数layersに指定する。前掲のリスト4-1を見ると、(tf.keras.layersモジュール階層の)Denseクラスのコンストラクターを利用して、インスタンスを生成していることが分かる。このコンストラクターは、
__init__(
units,
activation=None,
**kwargs
)
と定義されており(※不要な引数は説明を割愛)、各引数の意味は以下のとおりである。
- 第1引数のunits: ユニット(=ニューロン)の数を指定する。今回は、先ほどの定数LAYER1_NEURONSを指定すればよい
- 第2引数のactivation: 活性化関数を指定する。今回はtanh関数を使用するので、文字列で「tanh」と指定する。Kerasでは代表的な活性化関数は事前に定義されており(詳細後述)、文字列で指定するだけで済む。用意されていない場合は、独自の計算式をここに指定することもできる
- 第3引数のkwargs: 複数のキーワードとその値を指定できる。使えるキーワードは幾つかあるが(※不要なキーワードは説明を割愛)、その一つがinput_shapeで、もう一つがweightsである
- キーワード「input_shape」: 入力の形状をタプル値で指定する。今回は、先ほどの定数INPUT_FEATURESを指定すればよい。ただし、タプル型にするため(INPUT_FEATURES,)とタプル要素の最後に「,」を入れることで、タプル値と明示する必要が文法上ある
- キーワード「weights」: 「重み」の2次元配列値と「バイアス」の1次元配列値を、リスト値にまとめて指定する。今回は、[weight_array, bias_array]というリスト値を指定している。通常のニューラルネットワークでは、重みとバイアスは自動的に決まるもので、今回のように固定的な初期値を指定する必要はない(リスト4-1のような指定は説明のためのもので特殊な書き方である)
以上で、ニューロンのモデル定義は完了だ。まずはここまでをしっかりと押さえてほしい。後述のニューラルネットワークのモデル定義はこれを拡張していくだけなので、今回の説明は上記のコードが理解できることが鍵だ。
モデルへの入力と出力(フォワードプロパゲーション)
さて、それではこのモデルに入力を与えてみよう。今回は、先ほどの手計算の例と同じように座標(1.0、2.0)の1つだけをデータとする。前掲のリスト4-1では、1行2列(=行がデータの数、列が入力の数となっている)の2次元配列値を作り、X_dataという変数に代入している。そのX_dataを引数に指定して、modelオブジェクトのpredict()メソッドを呼び出している。
predict()メソッドは、上記で行った「ニューロンからの出力」の計算を自動的に実行し、戻り値としてモデルからの出力を返す。リスト4-1では、戻り値はprint()メソッドで出力しているので、Colab上のコードセルの下に[[0.7615942]]と出力されるはずだ(※なお、[[……]]と数値が多重カッコで囲まれているのは、この出力がNumPyの多次元配列値だからだ)。この数値は、前述の手計算で示した出力値の約0.76と全く同じであることを確認してほしい。
上記のコード例のように、モデルにデータを入力し、内部で何らかの変換をしてから、新たな出力値を得る流れ(プロセス)は、フォワードプロパゲーション(Forward Propagation)と呼ばれる。
以上でニューロンの解説は完了だ。続いて、ニューラルネットワークを見てみよう。
(4)“手法”の選択とモデルの定義: ニューラルネットワーク
単純なニューラルネットワークは、先ほどのニューロン(基本単位)をたくさんつなげてネットワーク化しただけのものである。先ほどのニューロンをキッチリと押さえていれば難しくない。
では、どのようなネットワーク構造にすればよいのか? これについて見ていこう。
Playgroundによる図解
ニューラルネットワークの基本形
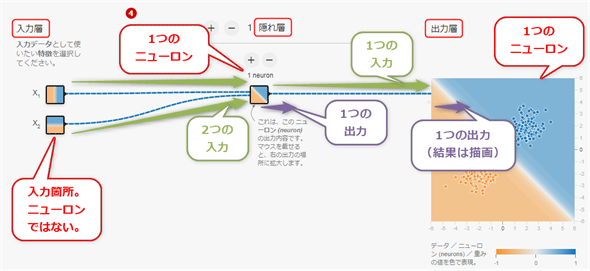
ニューラルネットワークの基本形は、入力層/隠れ層/出力層(Input layer/Hidden layer/Output layer)という3層構造を形成することである(※隠れ層は、中間層:Intermediate layerとも呼ばれる)。図4-7の表示に示すように、Playground上での表示もその基本形となっていることを確認してほしい。
図4-7は、次のようなニューロンで構成されている
- 入力層: Χ1とΧ2という特徴がある
- 隠れ層: 1つのニューロンがある
- 出力層: 1つのニューロンがある
ニューラルネットワークの場合、入力層にある特徴は、データの入力箇所であり、厳密にはニューロンではない。つまり、入力層のΧ1やΧ2は次の隠れ層にある各ニューロンへの入力としてそのまま使われるだけなのだ(=活性化関数による変換は入力層では行われない)。
よって、先ほど「3層構造」と書いたが、ネットワークの見た目は3層でも、実質的には2層構造である。このように層の数え方は見方や考え方によって変わってしまうので注意してほしい。
ちなみに、前掲のリスト4-1でinput_shape=(INPUT_FEATURES,)という引数が書かれていたが、これがまさに「入力層(=入力の形状)」を意味する。
説明がしつこくなるが、図4-8では、隠れ層にあるニューロンと、出力層にあるニューロンの入力と出力の流れを矢印で表現してみた。なお、出力層の出力は、次のニューロンへの入力ではなく、結果表示に使われるだけとなり、右側に大きく決定境界の図として描画されている。
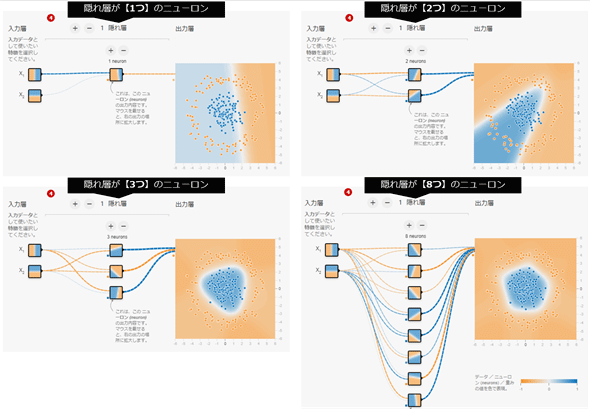
ニューロンの数を増やす
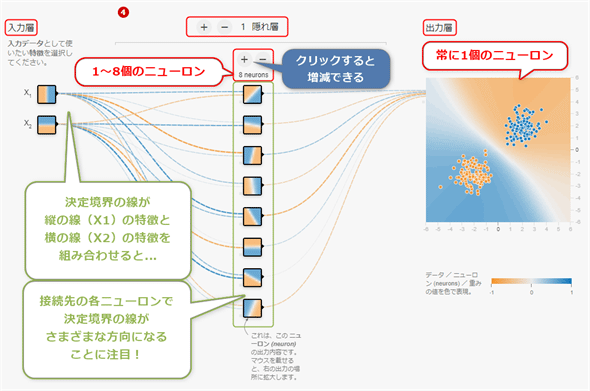
さて、先ほどは隠れ層も出力層も1つのニューロンしかなかった。ニューラルネットワークでは、それぞれニューロンの数を好きなだけ増やせる。Playgroundの提供機能では、出力層は1つのニューロン固定だが、隠れ層では8個までニューロンを増やせる(図4-9)。ちなみにPlayground上で実際に増やしてみる場合は、こちらを開いて[<数値> neurons]という表記の上にある[+]/[−]ボタンをクリックしてほしい。
図4-9の入力層にある2つのニューロンと、隠れ層にある8つのニューロンの、四角内の描画内容に注目してほしい。
入力層のΧ1には縦線が、Χ2には横線が描かれている。それに続く隠れ層の各ニューロンには、さまざまな方向の線が描かれている。これはつまり、縦線と横線をそれぞれ重み(前述の説明と同様に、w1やw2とする)を掛けて足し合わせると(=(w1 × Χ1)+(w2 × Χ2))、斜めなどのさまざまな方向の線が生まれるということだ。
これによって、単一のニューロンよりも少し複雑な問題が解決できるようになる。前述の通り、隠れ層が1つのニューロンだけでも斜めの線が生成できることが確認できた。よって、前回選択したデータセット「ガウシアン(Gaussian)」の分類問題は、これで解決できる。では、より複雑なデータセット「円(Circle)」の場合はどうだろうか?(図4-10)
隠れ層にある8つのニューロンの先にあるのは、出力層にある1つのニューロンである。この出力層のニューロンもまた、隠れ層にある8つのニューロンが持つさまざまな方向の線を入力として、それぞれに重みを掛けたうえで足し合わせた後の結果が出力/描画されることになる。方向の線が多ければ多いほど、多種多様な図形が描画できるようになる。例えば隠れ層のニューロンが、
- 1個だと「線」になる
- 2個だと「角のある領域」になる
- 3個だと「三角」が作れるようになる
- 4個だと「四角」が作れるようになる
- 5〜7個だと「五角形」〜「七角形」
- 8個が一番円らしい円を描画できる
はずだ。となれば、隠れ層に8つのニューロンを用意すれば、もっとも確実に問題を解決できそうである。
しかし、ニューロン数を増やせば増やすほど計算に時間がかかるようになる。つまり処理スピードが遅くなる。よって、ニューロン数はできるだけ少なくした上で問題解決できるほど、通常はより良い策だろう。実際に、「円」の分類は、3つのニューロンで三角形が描画できれば解決できる。図4-11は、隠れ層のニューロン数が1個/2個/3個/8個の場合に、「円」の分類問題がどのように解決されるかを示したものである。
当然ながら、左上の「1つ(=線)」や、右上の「2つ(=角のある領域)」では解決できない。右下の「8つ(=円に近い領域)」であれば解決できるが、これは計算処理に時間がかかる。左下の「3つ(=三角形)」であれば、問題もほぼ解決できるし、計算処理も比較的速い。よって、この問題例では、隠れ層にニューロンを3個用意すれば、最も効率が良さそうだと分かる。
このようにして、ニューロンの数を決定できる。ただし現実的には、この例のように隠れ層の各ニューロンの特徴をあらかじめイメージできる単純な問題ケースは少ないので、ニューロンの数を増やしたり減らしたりしながら試行錯誤する必要性が発生する。
以上がニューラルネットワークの基本形である。
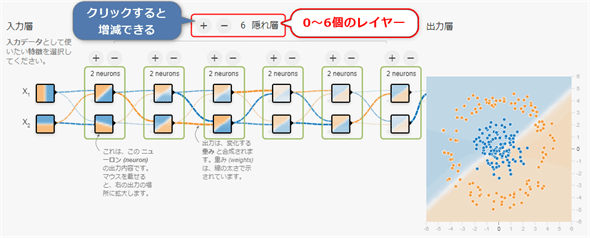
レイヤー(層)の数を増やす
さて、ニューラルネットワークの基本形は3層だったが、隠れ層は1層、2層、3層と好きなだけ増やせる、と紹介済みだ。Playgroundの提供機能では、隠れ層のレイヤーは6個まで増やせる(図4-12)。ちなみにPlayground上で実際に増やしてみる場合は、こちらを開いて[<数値> 隠れ層]という表記の左にある[+]/[−]ボタンをクリックしてほしい。なおニューロンの数は、先ほどと同様に、各レイヤーで8個まで増やせる。
隠れ層を2層以上に増やしたニューラルネットワークは、基本形と差別化して、ディープニューラルネットワーク(DNN:Deep Neural Network、もしくは深層ニューラルネットワーク)と呼ばれる。
では、隠れ層にあるレイヤーの数を増やすと、どんな効果があるのだろうか? これも先ほど説明したニューロン数を増やす理屈とほぼ同じである。例えば「三角」と「三角」を組み合わせると、非常に複雑な図形が表現できるようになるはずだ。要するに、レイヤーの数を増やせば増やすほど、高度で複雑な問題を解決できるようになるわけである。それこそが、DNNやディープラーニングの真価なのである。
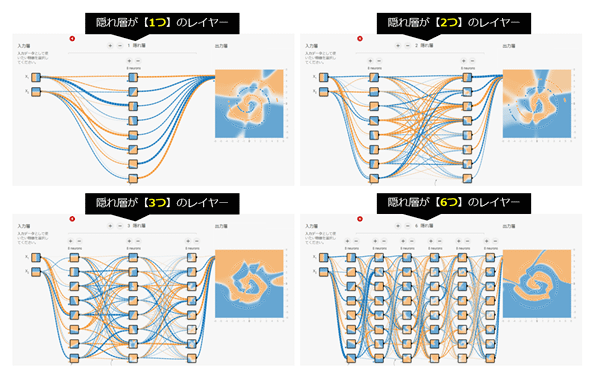
ただし、ニューロン数を増やす際と同様の問題を抱えていて、レイヤー数を増やせば増やすほど計算に時間がかかるようになり、処理スピードが遅くなる。よって、レイヤー数もできるだけ少なくして問題解決できるほど、通常はより良い策となるだろう。Playgroundで用意している分類問題のデータセットの中で一番複雑なのは「螺旋(らせん、Spiral)」であるが、この問題を解決するには、隠れ層のレイヤーの数が3つ以上になるとより解決しやすくなる。図4-13は、隠れ層のレイヤー数が1個/2個/3個/6個の場合に、「螺旋」の分類問題がどのように解決されるかを示したものである。
図4-13で各出力の背景色に注目すると、左上の「1つ」、右上の「2つ」、左下の「3つ」、右下の「6つ」の順でより正確に問題解決できるようになっていることが分かる。
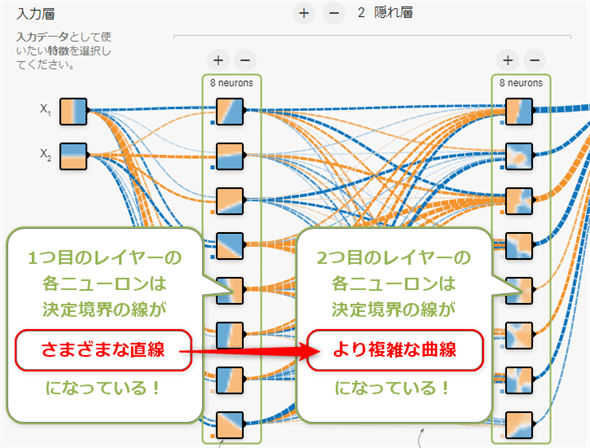
次の図4-14は、前掲の図4-13の右上にある「2つ」のレイヤーの例から、入力層と隠れ層の部分を抜き出したものである。各層内にある各ニューロンの、四角内の描画内容に注目してほしい。
1つ目のレイヤーにある各ニューロンの描画内容はさまざまな方向の直線だが、2つ目のレイヤーにある各ニューロンの描画内容はより複雑な曲線となっている。「レイヤーの数を増やせば増やすほど、より複雑な曲線や図形が表現できるようになり、高度な問題が解ける」と既に述べたが、これがその証左である。
以上がディープニューラルネットワークの基本である。
Pythonコードでの実装例
それでは、「ニューラルネットワーク」のモデルをPythonで定義してみよう。
モデルの定義
といっても、基本は先ほどのニューロンの定義方法と同じなので、そこからの差異を後述のリスト4-2では太字で示した。
ここではモデルのみを定義し、重みやバイアスの初期値は指定しない(通常は明示的に個別の値を指定しない。先ほどは特殊な書き方だった)。また、先ほどはデータを入力してフォワードプロパゲーションを体験したが、(同じような体験となるので)今度は行わないこととする。
ここでは、隠れ層のレイヤーを2つ用意し、各レイヤーのニューロンの数は3つずつにしてみよう。これは、次のようなコードになる。
# ライブラリ「TensorFlow」のtensorflowパッケージを「tf」という別名でインポート
import tensorflow as tf
# ライブラリ「NumPy」のnumpyパッケージを「np」という別名でインポート
import numpy as np
# 定数(モデル定義時に必要となる数値)
INPUT_FEATURES = 2 # 入力(特徴)の数: 2
LAYER1_NEURONS = 3 # ニューロンの数: 3
LAYER2_NEURONS = 3 # ニューロンの数: 3
OUTPUT_RESULTS = 1 # 出力結果の数: 1
# 今度は重みとバイアスのパラメーターは指定しない(通常は指定しない)
# 積層型のモデルの定義
model = tf.keras.models.Sequential([
# 隠れ層:1つ目のレイヤー
tf.keras.layers.Dense(
input_shape=(INPUT_FEATURES,), # 入力の形状(=入力層)
units=LAYER1_NEURONS, # ユニットの数
activation='tanh'), # 活性化関数
# 隠れ層:2つ目のレイヤー
tf.keras.layers.Dense(
units=LAYER2_NEURONS, # ユニットの数
activation='tanh'), # 活性化関数
# 出力層
tf.keras.layers.Dense(
units=OUTPUT_RESULTS, # ユニットの数
activation='tanh'), # 活性化関数
])
前掲のリスト4-1で示した「ニューロンのモデル設計」では、(tf.keras.layersモジュール階層の)Denseクラスのコンストラクターが1つだけだった。上掲のリスト4-2で示した「ニューラルネットワークのモデル設計」では、3つに増えている。隠れ層に2つ目のレイヤーと出力層が追加されたからだ。
なお、隠れ層の1つ目のレイヤーには、「入力層のデータ入力箇所」を意味するキーワード「input_shape」が指定されているが、それ以降のレイヤーでは、前のレイヤーからデータが流されるため、このキーワード指定が不要になっていることに注意してほしい。
他は特に難しいところはないだろう。このコード例は、4層で構成される「ディープニューラルネットワーク」となっている。3層の「ニューラルネットワークの基本形」にするには「隠れ層:2つ目のレイヤー」の部分をカットすればいいし、逆に5層以上にするには「隠れ層:2つ目のレイヤー」の部分を3つ目、4つ目と増やしていけばよいだけである。
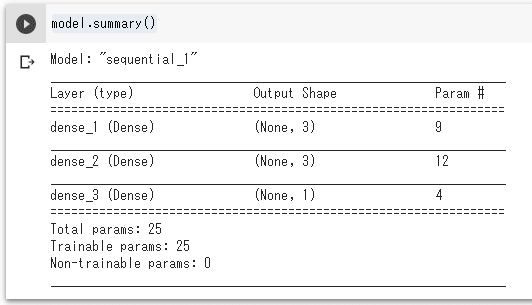
ちなみにKerasでは、確認用にモデルの概要を出力することもできる。これには、model.summary()というコードを実行するだけだ。
念のため、図4-15の内容も順に説明しておこう。
Keras内では「sequential_1」という名前のモデルが生成されており、「dense_1」という名前のレイヤー(=隠れ層:1つ目のレイヤー)の他、「dense_2」(=隠れ層:2つ目のレイヤー)、「dense_3」(=出力層)の、合計3つのレイヤーがあることが分かる。
出力形状(Output Shape)は、順に3個、3個、1個となる。
入力層から2つ目のレイヤーへの接続線(=重み)の数は2×3=6個で、バイアスの数は3個となるため、合計9個が「dense_1」のパラメーター数(Param #: Parameter number)となる。同様に計算すると、「dense_2」のパラメーターは合計12個、「dense_3」のパラメーターは合計4個である。
パラメーター数をまとめると、9+12+4=25個がパラメーターの総数(Total params)となり、学習/訓練可能なパラメーター数も25個である(※訓練不可能は0個。通常は訓練可能だが、必要があるときは訓練不可能にしてパラメーター値を“フリーズ”する機能がKerasにはある)。
ニューラルネットワークのモデル定義方法の基礎は以上で完了である。
Playgroundの上部にある「(4)手法” の選択: モデルの定義」を見ると、活性化関数と正則化を指定できる。その隣にある「(5)“学習方法” の設計: モデルの生成」には学習率や損失関数、最適化、バッチサイズなどがある。これらは学習方法をカスタマイズ/調整するためのもので、ハイパーパラメーターと呼ばれている。なお、ここまでに説明してきたニューロンやレイヤーの数もハイパーパラメーターの一種である。
本稿では最後に、活性化関数と正則化について簡単に紹介して終わりとする。
(4)“手法”の選択とモデルの定義: 活性化関数
まずは活性化関数から説明しよう。
Playgroundによる図解
活性化関数
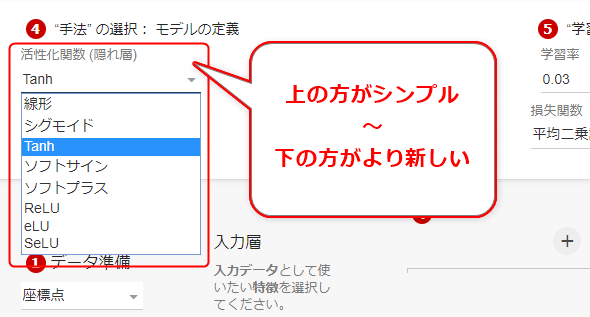
まずはPlaygroundを開いて、図4-16に示すように[活性化関数 (隠れ層)]欄のプルダウンリストを開いて見よう。するとたくさんの活性化関数が表示される。
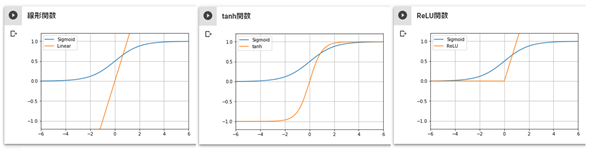
活性化関数については、既にシグモイド関数とtanh関数を紹介した。これら以外にも、研究によってより良いものが次々と考案され続けている。ここでは、代表的なものとしてシグモイド関数とtanh関数の他に、線形関数とReLU関数も取り上げて比較してみよう(図4-17)。
違いが分かりやすいように、シグモイド関数を比較対象として、線形関数/tanh関数/ReLU関数の3つを表示した。なお、活性化関数は中身の数式よりも、その数式がどのような形の線を描くのかを意識することが重要である。
シグモイド関数は、−∞〜+∞の数値を0.0〜1.0の範囲の数値に変換する、と説明済みだ。
一方、線形関数は値を変換せずにそのまま出力する。
tanh関数も説明済みで、−1.0〜1.0の範囲の数値に変換する。
ReLU関数は、0.0〜+∞の範囲の数値に変換する。
どの線形関数を使うかは、実際に使ってみて試行錯誤するしかないが、基本的に、
線形関数 < シグモイド関数 < tanh関数 < ReLU関数
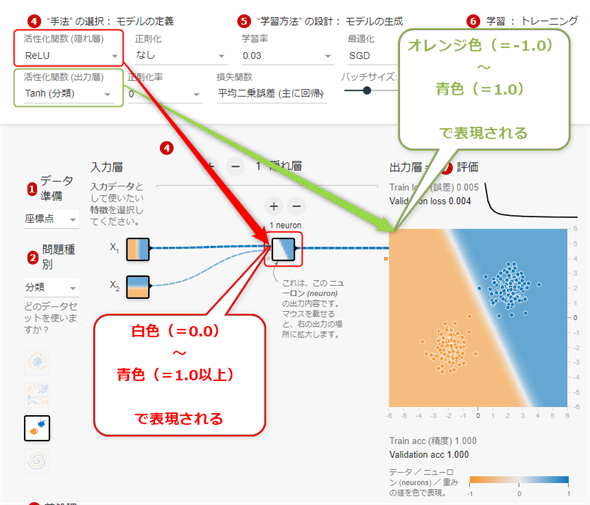
の順に効率的に学習できる可能性が高い。ちなみに、例えばReLU関数のように最小値が0.0になる場合は、中間の隠れ層の各ニューロンは-1.0などのマイナス値が出力できないため、オレンジ色(=-1.0)が表現できず、白色(=0.0)〜青色(=1.0以上)で表現されることになるため、注意してほしい(図4-18)。
なお、図4-18にも示した[活性化関数 (隠れ層)]欄のプルダウンリストでは、分類問題の場合、「Tanh関数」しか選択できないようにしてある。これは、最終的な出力値をオレンジ色(=-1.0)〜青色(=1.0)の範囲で表現したいためである。
Pythonコードでの実装例
前述の通り、活性化関数を指定する箇所は、(tf.keras.layersモジュール階層の)Denseクラスのコンストラクターの引数「activation」である。リスト4-1やリスト4-2では「tanh」と記述した。この文字列を指定したい活性化関数の名前に書き換えるだけである。
リスト4-3では、実際に「sigmoid」という記載に変更している。ただし、全ての隠れ層に対する記載を変更する必要があるため、ACTIVATIONという定数に切り出してから記載を変更した。なお、前後のコードは全く同じになるので省略している。
# ……省略……
# 定数(モデル定義時に必要となる数値)
# ……省略……
ACTIVATION = 'sigmoid' # 活性化関数(ここを書き換える): シグモイド関数
model = tf.keras.models.Sequential([
# 隠れ層:1つ目のレイヤー
tf.keras.layers.Dense(
input_shape=(INPUT_FEATURES,), # 入力の形状(=入力層)
units=LAYER1_NEURONS, # ユニットの数
activation=ACTIVATION) # 活性化関数
# ……省略……
])
Playgroundで選択可能な活性化関数は、Kerasでも対応している。具体的には、以下のものを文字列で記述できる(※一部の関数は本稿の内容をできるだけシンプルにするために説明していない。この他、「softmax」なども記述可能である)。
- linear(線形)
- sigmoid(シグモイド)
- tanh(Tanh)
- softsign(ソフトサイン)
- softplus(ソフトプラス)
- relu(ReLU)
- elu(eLU)
- selu(SeLU)
(4)“手法”の選択とモデルの定義: 正則化
次に正則化について説明しよう。
Playgroundによる図解
正則化
正則化(Regularization、Regularizer)は、主に過学習(後述)を防ぐためのテクニックの一つである。過学習を防ぐテクニックとして他にはドロップアウト(Dropout)が有名であるが、Playgroundにはドロップアウト機能がないため、今回は説明を割愛する。
そもそも過学習(overfitting、過剰適合)とは、訓練データに特化して学習し過ぎると、それがかえって未知のデータ(テストデータなど)には適合しなくなることである。例えるなら、演歌ばかり歌っていると、どんな曲を歌うときでも、こぶしを利かせて歌ってしまうイメージだ。
正則化には、主に下記の2種類がある。
- L1: 不要なニューロンを抑制/排除して、モデルの中身をシンプル(疎)にする
- L2: 重みパラメーターにペナルティを加えて、学習し過ぎないようにする
特に「L2」による重みの正則化は、ニューラルネットワークでは重み減衰(Weight Decay)と呼ばれ、よく利用される。どちらを使うかはケースバイケースだが、基本的にはL2を使うことが多いだろう。
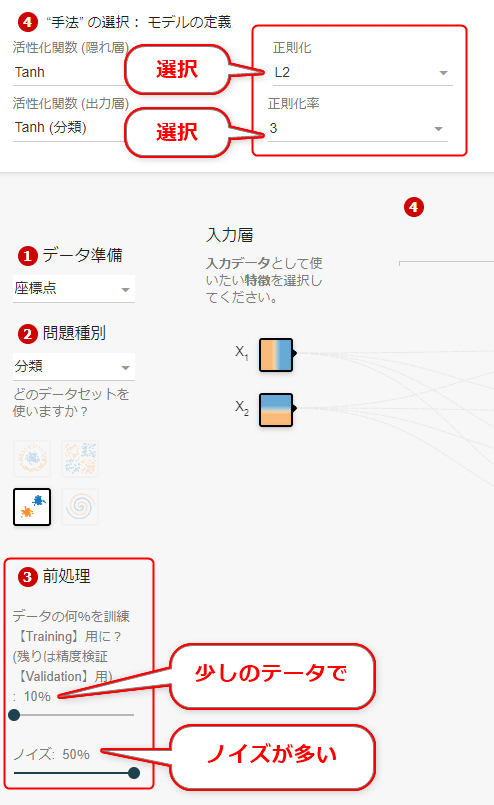
過学習が発生しやすいのは、データに(外れ値などの)ノイズが多く、しかも訓練データの数が少ない場合である。この状況を作るには、Playgroundを開いて、前回説明した[(3)前処理]の箇所で、
- データ分割: 訓練用を10%
- ノイズ: 50%
などと設定すればよい。実際にこれを行っているのが、図4-19である。
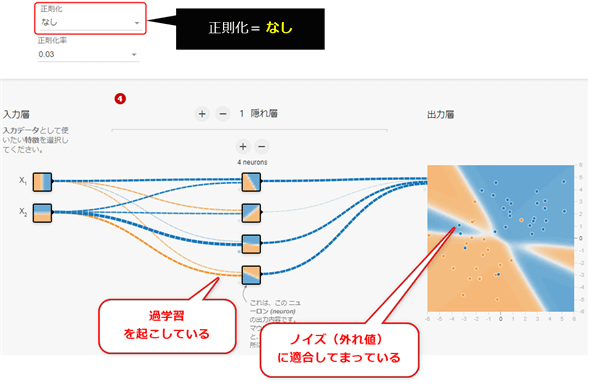
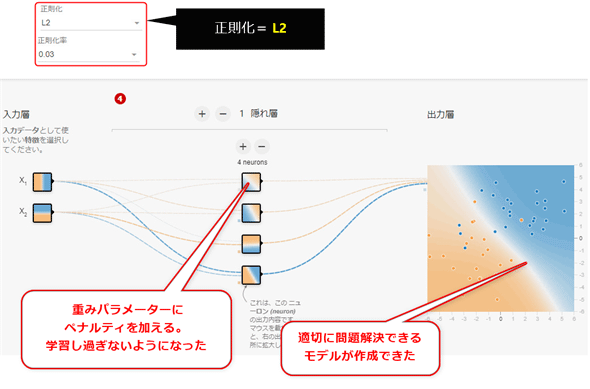
正則化は、上部で指定でき(図4-19)、「なし」「L1」「L2」から選択できる。図4-20-1は「なし」、図4-20-2は「L1」、図4-20-3は「L2」を選択した場合の、ニューラルネットワークの例である。正則化率は、全て「0.03」を指定した(詳細後述)。
説明した通り、正則化「なし」は過学習を起こしており、未知のデータを入れると不正解を多く出す可能性のあるモデルとなってしまっている。
L1正則化を行うと、隠れ層のニューロンが白色になっているものがあり、ニューロンが抑制/排除されているのが分かる。その結果、モデルがシンプルになり、適切に問題が解決できるようになっている。
L2正則化を行うと、「なし」と比べて接続線(=重み)が細く薄くなっており、学習し過ぎないようになったことが分かる。その結果、適切に問題が解決できるようになっている。
以上が正則化の効果だ。
正則化率
後は正則化率であるが、0.1〜0.001など任意の数値を指定できる。先ほどの例(前掲の図4-20-3)では0.03を指定することで、うまく過学習を軽減できた。それ以外の正則化率、具体的には0.003/0.03/0.3/3を指定した場合の学習結果の違いを、図4-21にまとめた。
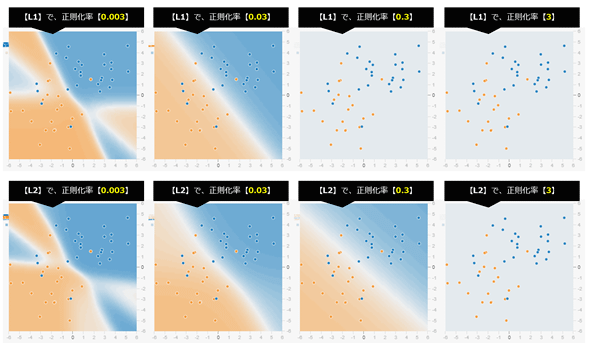
図4-21 正則化「L1」(上段)と「L2」(下段)で正則化率の違いの比較(0.003/0.03/0.3/3の場合)
※いずれも1000回(学習単位は「エポック」と呼ばれる)学習した結果(背景)の比較である。
まず、左端の0.003では、L1もL2も数値が小さすぎて、ほとんど学習結果に影響していないことが分かる。
次の0.03は、L1もL2もほどよく学習できているようである。
その次の0.3は、L1は背景が白色になっており、全く学習できなくなってしまっている。L2はそこそこ学習できているが、前の0.03よりも色が薄くなってしまった。
右端の3は、L1もL2も数値が大きすぎて、全く学習できていない。
このように、正則化率も程よい数値を試行錯誤で模索する必要がある。だいたいは0.01付近を中心に探すとよい。
Pythonコードでの実装例
正則化についてもコードを示しておこう。重みの正則化を指定する箇所は、(tf.keras.layersモジュール階層の)Denseクラスのコンストラクターの引数「kernel_regularizer」である。
リスト4-4では、実際に「L2正則化で、正則化率は0.03」を指定している。ただし、全てのレイヤー(隠れ層と出力層)に対して追記する必要があるため、REGULARIZATIONという定数に切り出して指定した。なお、前後のコードはこれまでと全く同じになるので省略した。
# ……省略……
# 定数(モデル定義時に必要となる数値)
# ……省略……
REGULARIZATION = tf.keras.regularizers.l2(0.03) # 正則化: L2、 正則化率: 0.03
model = tf.keras.models.Sequential([
# 隠れ層:1つ目のレイヤー
tf.keras.layers.Dense(
input_shape=(INPUT_FEATURES,), # 入力の形状(=入力層)
units=LAYER1_NEURONS, # ユニットの数
activation=ACTIVATION, # 活性化関数
kernel_regularizer= REGULARIZATION) # 正則化
# ……省略……
])
このように、引数「kernel_regularizer」には、(tf.keras.regularizersモジュール階層の)l2()関数を指定すればよい。L1正則化の場合は、l1()関数である。いずれの関数も引数に、正則化率を指定する。
なお、l1()/l2()関数には、0.01がデフォルト引数で指定されている。そのため、正則化率を0.01としたい場合は、引数なしで呼び出せる。
今回は、少し長くなったが、(4)のニューラルネットワークのモデルの定義方法と、活性化関数、正則化について説明した。次回後編では、(5)〜(8)の学習、評価、テストについて説明する。
Copyright© Digital Advantage Corp. All Rights Reserved.