第3回 ディープラーニング最速入門 ― 仕組み理解×初実装(後編):TensorFlow 2+Keras(tf.keras)入門(1/3 ページ)
いよいよ、ディープラーニングの学習部分を解説。ニューラルネットワーク(NN)はどうやって学習するのか、Pythonとライブラリではどのように実装すればよいのか、をできるだけ簡潔に説明する。
前々回、ディープラーニングの大まかな流れを、下記の8つの工程で示した。
- (1)データ準備
- (2)問題種別
- (3)前処理
- (4)“手法” の選択: モデルの定義
- (5)“学習方法” の設計: モデルの生成
- (6)学習 : トレーニング
- (7)評価
- (8)テスト
このうち、(1)〜(4)を前回までに説明した。引き続き今回は、(5)〜(8)を解説する。いよいよ今回で完結である。それではさっそく説明に入ろう。※脚注や図、コードリストの番号は前回からの続き番号としている(前編・中編・後編は、切り離さず、ひとまとまりの記事として読んでほしいため連続性を持たせている)。
(5)“学習方法” の設計とモデルの生成: 損失関数
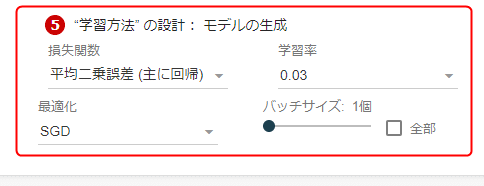
前回の(4)でニューラルネットワークのモデルが定義できた(※前回示したように本連載ではKerasを使用)。次に(6)学習を行うわけだが、その前に「どのように学習するか」の決定、つまり「(5)“学習方法”の設計」をしておく必要がある。具体的には、第1回から使っている「ニューラルネットワーク Playground - Deep Insider」(以下、Playground)の上部にある図5-1の3カ所、
- 損失関数
- 最適化
- 学習率
がそれに該当する。なお、バッチサイズは「最適化」の節で軽く触れ、後述の「学習」の章で詳しく説明する。
この3つを設定すればよいわけだ。1つずつ説明していく。まずは損失関数を説明しよう。今回も、まずはPlaygroundを使って図解で説明し、その後で具体的なコード実装方法を紹介する。
Playgroundによる図解
Playgroundを開いて、上部にある(5)の[損失関数]欄で「平均二乗誤差」を選択する(図5-2)。
回帰問題/分類問題でよく使われる損失関数
「損失関数」や「平均二乗誤差」の意味は後述するが、平均二乗誤差が最も代表的な損失関数(意味は後述)である。分類問題か回帰問題かによって、よく使われる損失関数に違いがある。選択肢に「(主に回帰)」「(2クラス分類)」「(多クラス分類)」というカッコ書きがあるが、その違いを示したものである。まとめておくと、
- 平均二乗誤差(MSE:Mean Squared Error)=回帰問題でよく使う損失関数
- 交差エントロピー誤差(Cross Entropy Error)=分類問題でよく使う損失関数
ということになる。今回は分類問題を扱うが、最も有名な「平均二乗誤差」を使う。交差エントロピー誤差については説明を割愛する(※「平均絶対誤差」については、後で「平均二乗誤差」との違いを示すので、それを参考にしてほしい)。
誤差とは
いずれの損失関数も、「誤差」を調べるための関数(=入力を受けて、何らかの計算をして、出力するもの)であると、字面から分かるだろう。誤差(エラー: error)とは、言葉通りの意味で、計算で得られた値と、正解の値にある、「ズレ」のことである。
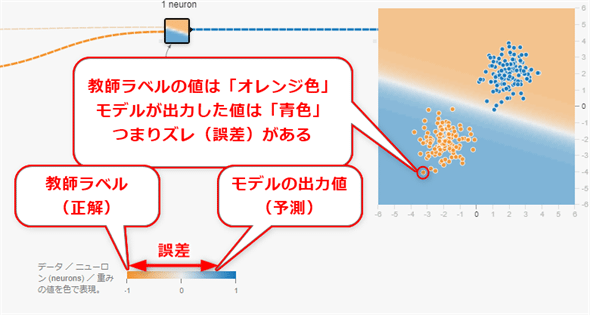
機械学習の場合、ニューラルネットワークのモデルに入力した値が、フォワードプロパゲーション(順伝播)によって処理され、出力される(※前回解説した)。その出力結果の値と、正解を示す教師ラベル(※第1回で解説した)の値がどれくらいズレているか(=誤差)を調べるわけである(図5-3)。
あとは、全てのデータに対して誤差を調べていき、それを平均すれば、モデルの平均的な誤差が算出できると考えられるだろう。しかし実は、その計算方法ではうまくいかない。
なぜ「二乗」するか
例えば3つのデータがあり、それぞれの誤差が「+1.2」「-1.0」「-0.2」だったとしよう。「平均的に正解からどれくらいズレているか」を見たい場合に、これらを単純に全部合計してデータ数の3で割ってしまうと「+1.2-1.0-0.2=0.0」となってしまう。つまりズレが全くないことになってしまう。これは違う。
ズレを計測するためには、距離が重要であるため、マイナスはプラスとして計算、つまり絶対値化して計算する必要がある。これを行うのが、前掲の「平均絶対誤差」(MAE:Mean Absolute Error)である。
しかし数学や統計学の世界では、実は絶対値は扱いにくい。マイナスをプラスにする計算方法としては、絶対値の他にも、二乗計算がある(※数字の右肩に小さく「2」と書く、中学で学ぶ計算式で、例えば-2の二乗は+4となる)。そして、二乗計算では、特に微分計算(高校で習う計算方法)がしやすくなって便利という利点もある。そのため数学や統計学では、マイナスをプラスにする計算には二乗がよく用いられるのだ。
「誤差を二乗してから平均を取る計算」である平均二乗誤差*2は、このような理由からニューラルネットワークで代表的な「損失関数」となっている。なお、平均二乗誤差などの計算結果の数値は、損失(ロス: loss)と呼ばれる。この損失を求めるための関数であるため、損失関数(Loss Function)と呼ばれるのである。
*2 平均二乗誤差の「平均」とは、誤差の二乗和を「そのデータ数で割る」ことを意味する。しかし書籍などの説明によっては「2」で割る、いわば「“1/2”二乗和誤差」(SSE:Sum of Squared Error)が用いられている。これは、「二乗した変数を微分した際に係数として2が出てくるので、それに1/2を掛けたら1になって計算が楽になるよね」という、いわばマジックナンバーなのである。例えばニューラルネットワークの学習をフルスクラッチで作ってみる場合、この“1/2”二乗和誤差を使うと実際に楽である。ちなみに、Playgroundの損失関数も、実は平均二乗誤差ではなく“1/2”二乗和誤差を用いているが、本稿のコード説明との一貫性を出すため、表記は「平均二乗誤差」とした。
Pythonコードでの実装例
では、損失関数として「平均二乗誤差」(Mean Squared Error)をコードで実装してみよう。tf.keras(=TensorFlow同梱のKeras)で、損失関数の計算式を独自に定義するのは難しくないが、Kerasには代表的な損失関数があらかじめ用意されており、しかも文字列で指定するだけである(※前回説明した活性化関数と同じ)。今回は定数として切り出し、リスト5-1のように記載することにした。
# 定数(学習方法設計時に必要となるもの)
LOSS = 'mean_squared_error' # 損失関数: 平均二乗誤差
Playgroundで選択肢に挙げている損失関数は、Kerasでも対応している。具体的には、以下のものを文字列で記述できる(※一部の関数は本稿の内容をできるだけシンプルにするために説明していない)。
- mean_squared_error(平均二乗誤差)
- mean_absolute_error(平均絶対誤差)
- binary_crossentropy(交差エントロピー誤差: 2クラス分類)
- categorical_crossentropy(交差エントロピー誤差: 多クラス分類)
(5)“学習方法” の設計とモデルの生成: 最適化
次に最適化を説明しよう。
Playgroundによる図解
Playground上では、(5)の[最適化]欄で「SGD」を選択する(図5-4)。バッチサイズは後述するが、ここでは何も考えずに「1」を選択してほしい。
「最適化?」「SGD?」……疑問がいっぱいあるだろう。まずは最適化とは何かから説明する。
最適化とは
最適化(Optimization)とは、言葉通り、最も適している状態に変えることである。では、「ニューラルネットワークにおいて、最も適している状態とは、どのようなことか?」というと、先ほどの損失(loss)を極限まで最小化できていることを指す。
つまり、先ほどの損失関数(平均二乗誤差)の結果の数値をできるだけ0に近づければよいわけである。その最適化手法として、さまざまな方法(最適化アルゴリズムと呼ぶ)が考えられている。その基本が、「勾配法」なのである。
勾配法とは
勾配法(Gradient method)とは、勾配(gradient)、つまり坂道を下っていく(descent)ように計算することで最適化を行う手法のことである。
先ほど選択した「SGD」は、この勾配法の一種で、確率的勾配降下法(SGD:Stochastic Gradient Descent)を意味する。SGDは、最適化の計算を確率論を用いて(=stochasticに)実行することで、全部一括(=バッチと呼ぶ)の訓練データではなく、1つ、もしくは複数セット(=ミニバッチと呼ぶ)の訓練データで学習して、その単位ごとに重みやバイアスを更新していく方法である(※詳しくは「バッチサイズ」の章で解説する)。先ほど[バッチサイズ]で「1」を選択したのは、このためである。
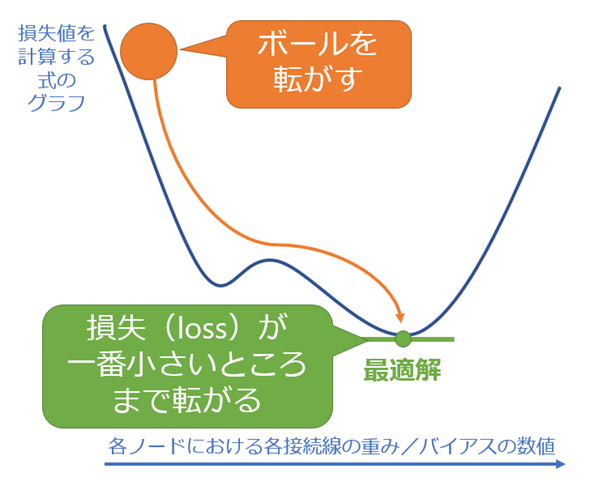
最適化を理解するキモは、「勾配法」を理解することにある。上記の説明では「何を言っているか」が分からないと思うので、まずは図5-5を見てイメージをしてもらおう。
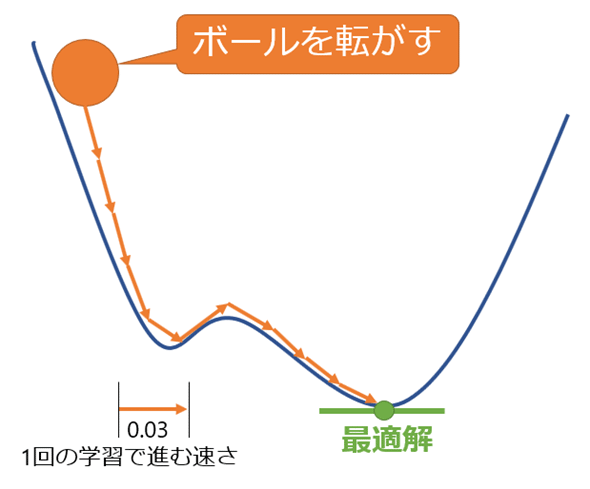
図5-5に示す青色の曲線が勾配(=坂道)である。その坂道の線の上を、オレンジ色のボールが進むように投げた、とイメージしてほしい。投げた(=学習した)回数だけ、ボールは進み、最終的に一番低い位置(=損失が一番小さい場所、最適解)まで転がっていく。ただし、この世界は無重力であり、重力によって自動的に一番低い位置に転がるわけではく、1回の学習によって少しずつ位置を変えていく、と考えてほしい。
ボールを投げる際には、青色の曲線上にある現在位置から見て、「坂道の左側が下りか、それとも右側が下りか」を判断、数学的に言うと「傾き」を判断して、左右どちらにボールを動かすかを決める。数学では、曲線における1地点(=ボールがある位置)の傾きは、微分によって計算できる。また、パラメーターが複数ある曲線の傾きは、偏微分によって計算できる。
【コラム】偏微分と線形代数と統計学
ディープラーニングの習得で、「偏微分が必修」となるのは、上記のように最適化の計算のためである。
また「線形代数も必修」とされるのは、大量のデータをまとめて計算する際に、線形代数の行列演算が必要になるためである。
偏微分や線形代数の計算は、TensorFlow/Kerasのようなライブラリが内部で行ってくれるので、単に実装するだけであれば、あまり気にする必要はない。しかし理論面を考える場合や、最適化アルゴリズムの違いを厳密に理解したい場合には、こういった数式の理解が必要となる。
さらに、統計学も最低、大学基礎教養レベル(統計検定2級レベル)の知識があった方が、ニューラルネットワークや機械学習の理論が理解しやすくなる。例えば最適化&勾配法は回帰分析や重回帰分析と同じ考え方がベースになっているなど、統計学をベースとした考えが多いからだ。
本稿の内容をマスターしたら、ぜひ長期戦で、数学や統計学の知識も増やしていってほしい。
Pythonコードでの実装例
では、最適化として「SGD」(確率的勾配降下法)をコードで実装してみよう。これも、Kerasには代表的な最適化アルゴリズム(Optimizer:オプティマイザ)があらかじめ用意されており、tf.keras.optimizersモジュール階層(=名前空間)のクラスを使うだけなので簡単である。
今回はクラス名を定数として切り出し、リスト5-2のように記載することにした。なお、クラスのコンストラクター(厳密には__init__関数)に指定する引数は後述する。
# (必要に応じて)TensorFlow v2の最新バージョンにアップグレードする必要がある
#!pip install --upgrade tensorflow
# ライブラリ「TensorFlow」のtensorflowパッケージを「tf」という別名でインポート
import tensorflow as tf
# 定数(学習方法設計時に必要となるもの)
OPTIMIZER = tf.keras.optimizers.SGD # 最適化:確率的勾配降下法
※本稿は、TensorFlow v2を前提とする。前回、TensorFlow v2の最新バージョンへのアップグレード方法を説明している。
Playgroundで選択肢に挙げている最適化アルゴリズム(オプティマイザ)は、Kerasでも対応している。具体的には、以下のものが使える(※代表的なもののみ掲載)。
- SGD(確率的勾配降下法)
- Adagrad
- RMSprop
- Adadelta
- Adam
- Adamax
- Nadam
※中身のアルゴリズムの説明は簡単ではないので、本稿では説明を割愛する。どれを使ってもよいが、まずは基本となるSGDを使ってみるとよい。
(5)“学習方法” の設計とモデルの生成: 学習率
続いて、非常に重要な「学習率」を説明しよう。
Playgroundによる図解
Playground上では、(5)の[学習率]欄で「0.03」を選択する(図5-6)。
「学習率」は、最適化と関連する設定事項であり、「1回の学習でニューラルネットワーク内の重みやバイアスを更新する量の調整値」を表す(=ハイパーパラメーターの一つ)。といってもよく分からないと思うので、これもボールを転がす例でイメージをしてもらうことにする。図5-7を見てほしい。
図5-7では、ボールを1回投げると、そのたびに、最適解に向かって少しずつ転がっていく。ボールのスピードが速いと大量に転がり、遅いと少ししか転がらない。そのボールを投げるスピードに該当する数値が、学習率(learning rate)なのである。
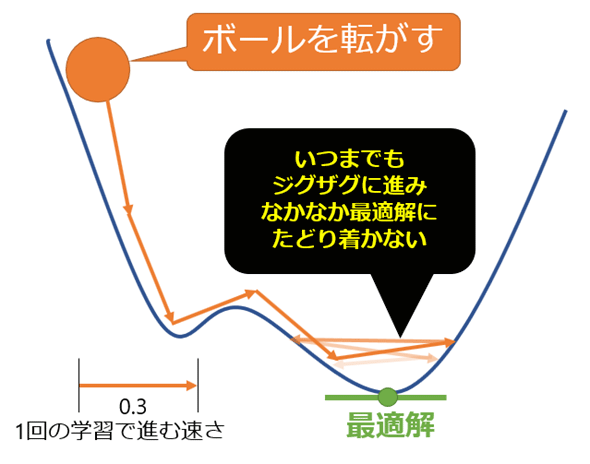
学習率には、0.1〜0.001など任意の数値を指定できる。大きい学習率を設定した方が、より速く学習できる。よって「大きい値の方がよいのでは」と思うかもしれないが、それはそれでなかなか学習が収束しない問題が発生したりするので、一概には言えない。例えば図5-7が学習率に0.03を指定した場合のイメージだとすると、図5-8は0.3を指定した場合のイメージである。
図5-8は矢印が長すぎるため、最適解を通り越して行きすぎてしまい、なかなか最適解にたどり着かない。その結果、最適解の近辺をいつまでもジグザグと行ったり来たりしてしまう。つまり、学習が最適解にきれいに収束しない問題が起こっているのである。
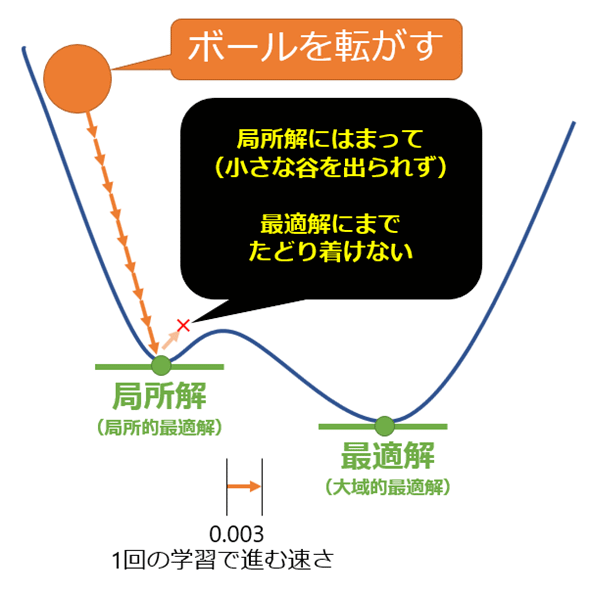
なら、「小さい値の方がよい」と思うかもしれないが、それだとなかなか学習が終わらない問題が発生したりするので、これも一概には言えない。それだけでなく、本当の最適解(global optimal solution、大局的な最適解)ではなく、局所的な最適解(local optimal solution、局所解、いわば「谷」)に収束して、その谷から抜け出せなくなる場合があるのだ(図5-9)。
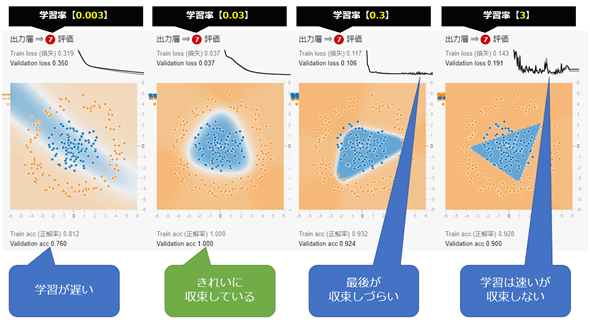
全ケース一律に当てはまる数値があるわけではないので、ケースバイケースで適切な学習率を試行錯誤しながら探す必要がある。だいたい0.1前後から数値を小さくしていく方向で探せばよい。できるだけ高速に処理できて、しかも精度がそこそこよい学習率が、一般的には「より良い学習率」と言えるだろう。参考までに、0.003/0.03/0.3/3を指定した場合の学習結果の違いを、図5-10にまとめた。
それぞれの結果の上部にある[Train loss]というのは「訓練データにおける損失」で、[Validation loss]は「精度検証データにおける損失」のことである。また、下部に表示されている[Train acc](acc=accuracy)というのは「訓練データにおける正解率」で、[Validation acc]は「精度検証データにおける正解率」のことである。正解率(精度)とは、言葉通り、モデルの出力結果が「何%正解を出すか」の数値である。
まず、左端の0.003では、学習が遅く、100回学習しただけでは[Train loss]が0.319などと0.0に近づききれていない。これはまだ学習途中を意味する。
次の0.03は、ほどよく学習できている。
その次の0.3は、[Train loss]のグラフの右端がギザギザとなっており、損失が大きくなったり小さくなったりと揺れている。これは、前述の「収束しない」に相当する現象である。
右端の3は、[Train loss]のグラフが激しくジグザグになっており、学習がうまく進んでいないことを表している。
Pythonコードでの実装例
では、学習率として「0.03」をコードで実装してみよう。この数値も定数として定義しておく(リスト5-3)。
# 定数(学習方法設計時に必要となるもの)
LEARNING_RATE = 0.03 # 学習率: 0.03
以上で、「損失関数」「最適化」「学習率」の定義が終わった。あとはこれらを使って、モデルを生成すればよい。その作業に入る前に、前回の復習として、モデル定義のコードを見てみよう。リスト5-4の内容は前回の説明を理解していれば分かるはずである。
# ライブラリ「TensorFlow」のtensorflowパッケージを「tf」という別名でインポート
import tensorflow as tf
# 定数(モデル定義時に必要となる数値)
INPUT_FEATURES = 2 # 入力(特徴)の数: 2
LAYER1_NEURONS = 3 # ニューロンの数: 3
LAYER2_NEURONS = 3 # ニューロンの数: 3
OUTPUT_RESULTS = 1 # 出力結果の数: 1
ACTIVATION = 'tanh' # 活性化関数(ここを書き換える): tanh関数
# 積層型のモデルの定義
model = tf.keras.models.Sequential([
# 隠れ層:1つ目のレイヤー
tf.keras.layers.Dense(
input_shape=(INPUT_FEATURES,), # 入力の形状(=入力層)
units=LAYER1_NEURONS, # ユニットの数
activation=ACTIVATION), # 活性化関数
# 隠れ層:2つ目のレイヤー
tf.keras.layers.Dense(
units=LAYER2_NEURONS, # ユニットの数
activation=ACTIVATION), # 活性化関数
# 出力層
tf.keras.layers.Dense(
units=OUTPUT_RESULTS, # ユニットの数
activation='tanh'), # 活性化関数(※tanh固定)
])
また、Kerasでは、学習結果を評価するための指標を、モデル生成時に指定しておく必要がある。回帰問題では損失を見ればよいだろうが、分類問題では「正解率は何%か」を示す精度(accuracy:正解率、正確度)も見たいだろう。Kerasでは、下記のような評価指標が評価関数(Evaluation Function)として用意されている(※代表的なもののみ掲載。それぞれの具体的な使い方の説明は割愛する)。
- accuracy(正解率)
- binary_accuracy(2クラス分類の正解率)
- categorical_accuracy(多クラス分類の正解率)
しかし今回は、モデルからの出力値が活性化関数の「tanh関数」により-1.0〜1.0で出力するようになっていることに注意してほしい。通常は、0.0〜1.0であるため、既存のbinary_accuracyでは正常に正解率が取得できない。そこで今回は、独自の評価関数を作成した。具体的にはリスト5-5のようになる。このようなKerasのカスタマイズ機能は、本稿の説明範囲を超えているので、詳細は説明しない。コード内のコメントを参考にしてほしい。
import tensorflow.keras.backend as K
def tanh_accuracy(y_true, y_pred): # y_trueは正解、y_predは予測(出力)
threshold = K.cast(0.0, y_pred.dtype) # -1か1かを分ける閾値を作成
y_pred = K.cast(y_pred >= threshold, y_pred.dtype) # 閾値未満で0、以上で1に変換
# 2倍して-1.0することで、0/1を-1.0/1.0にスケール変換して正解率を計算
return K.mean(K.equal(y_true, y_pred * 2 - 1.0), axis=-1)
それではモデルを生成する。これはリスト5-6のようなコードになる。
# 定数(学習方法設計時に必要となるもの)
LOSS = 'mean_squared_error' # 損失関数: 平均二乗誤差
OPTIMIZER = tf.keras.optimizers.SGD # 最適化: 確率的勾配降下法
LEARNING_RATE = 0.03 # 学習率: 0.03
# モデルを生成する
model.compile(optimizer=OPTIMIZER(learning_rate=LEARNING_RATE),
loss=LOSS,
metrics=[tanh_accuracy]) # 精度(正解率)
モデルの生成は、modelオブジェクトのcompileメソッドで行える。このメソッドは、
compile(
optimizer,
loss,
metrics=None
)
と定義されており(※不要な引数は説明を割愛)、各引数の意味は以下の通りである。
- 第1引数のoptimizer: 最適化アルゴリズムを指定する。今回は、先ほどの定数OPTIMIZERを指定すればよい
- OPTIMIZER定数の中身であるSGDクラスは、コンストラクターを呼び出してインスタンス化する必要がある。そのコンストラクターの引数には、learning_rateというキーワードで学習率が指定できる。今回は、先ほどの定数LEARNING_RATEを指定すればよい。指定しない場合は、既定値の0.01が使われる
- 第2引数のloss: 損失関数を指定する。これも、先ほどの定数LOSSを指定すればよい
- 第3引数のmetrics: 評価関数を指定できる(※評価については後述する)。分類問題では、典型的には'accuracy'と文字列で評価関数を指定すればよい。ただし今回は自作のtanh_accuracy関数を指定している。なお、評価関数は複数指定できるので、リスト値にして指定する必要がある
以上でモデルの生成は完了だ。
(6)学習:トレーニング
Copyright© Digital Advantage Corp. All Rights Reserved.
![図5-2 [損失関数]で「平均二乗誤差」を選択](https://image.itmedia.co.jp/ait/articles/1912/16/di-05-2.gif)
![図5-4 [最適化]で「SGD」を選択](https://image.itmedia.co.jp/ait/articles/1912/16/di-05-4.gif)
![図5-6 [学習率]で「0.03」を選択](https://image.itmedia.co.jp/ait/articles/1912/16/di-05-6.gif)