第3回 PyTorchによるディープラーニング実装手順の基本:PyTorch入門(1/2 ページ)
いよいよ、PyTorchを使ったディープラーニングの流れを通して全体的に説明する。ミニバッチ学習を手軽にするデータローダーから始めて、ディープニューラルネットワークのモデル定義、オプティマイザを使った学習、損失/正解率の出力やグラフ表示といった評価までを解説。
本連載の第1回〜第3回までは続きものとなっている。
- 第1回: 難しくない! PyTorchでニューラルネットワークの基本(前々回)
- 第2回: PyTorchのテンソル&データ型のチートシート(前回)
- 第3回: PyTorchによるディープラーニング実装手順の基本(今回)
前々回はPyTorchの核となる部分を、前回はPyTorchの基礎部分といえる「テンソルとデータ型」の説明を行った。今回は、4層のディープニューラルネットワークを題材に、PyTorchによる基本的な実装方法と一連の流れを解説する。
全3回の大まかな流れは以下の通りである。
(1)ニューロンのモデル定義
(2)フォワードプロパゲーション(順伝播)
(3)バックプロパゲーション(逆伝播)と自動微分(Autograd)
(4)PyTorchの基礎: テンソルとデータ型
(5)データセットとデータローダー(DataLoader)
(6)ディープニューラルネットのモデル定義
(7)学習/最適化(オプティマイザ)
(8)評価/精度検証
このうち、(1)〜(3)は前々回、(4)は前回で説明済みである。今回は(5)〜(8)を説明する。それでは、前々回の核となる部分を簡単に振り返ったうえで、さっそく今回の説明に入ろう。※脚注や図、コードリストの番号は前回からの続き番号としている(第1回〜第3回は、切り離さず、ひとまとまりの記事として読んでほしいため連続性を持たせている)。
PyTorchの「核」部分の振り返り
簡単にポイントだけまとめると、
- class NeuralNetwork(nn.Module):でニューラルネットワークのクラスを定義する
- model = NeuralNetwork()でモデルをインスタンス化する
- y_pred = model(X_data)で「入力データ」→「モデル」→「出力の予測結果」の推論を行う
- criterion = nn.MSELoss(); loss = criterion(y_pred, y_true)で、損失を計算する
- loss.backward()で、バックプロパゲーションを行う
という5つの手順が核部分である。実践活用するための手順として残りは、
- 訓練/最適化
- 評価/精度検証
が残っており、今回説明する。まずはデータから説明していく。
(5)データセットとデータローダー(DataLoader)
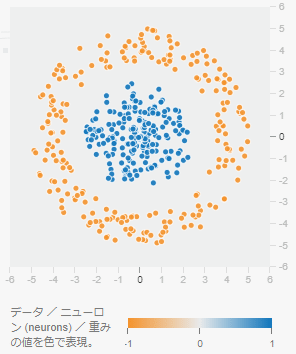
座標点データの生成
データは、シンプルな座標点データを生成して使う(図5)。この座標点データは、「ニューラルネットワーク Playground - Deep Insider」(以下、Playground)と同じ生成仕様となっている。
モデルへの入力データは、
- 座標(横のX軸上の値、縦のY軸上の値)
である。
教師ラベルは、
- -1.0=オレンジ色
- 1.0=青色
の点で示されている。
この座標点データは、第1回で紹介した連載記事「前編: 初めてのニューラルネットワーク実装、まずは準備をしよう」で使ったものと同じなので、詳しい内容や使い方はそちらを参照してほしい。
今回は次のようなコードを記述した。
# 座標点データを生成するライブラリのインストール
!pip install playground-data
# playground-dataライブラリのplygdataパッケージを「pg」という別名でインポート
import plygdata as pg
# 設定値を定数として定義
PROBLEM_DATA_TYPE = pg.DatasetType.ClassifyCircleData # 問題種別:「分類(Classification)」、データ種別:「円(CircleData)」を選択
TRAINING_DATA_RATIO = 0.5 # データの何%を訓練【Training】用に? (残りは精度検証【Validation】用) : 50%
DATA_NOISE = 0.0 # ノイズ: 0%
# 定義済みの定数を引数に指定して、データを生成する
data_list = pg.generate_data(PROBLEM_DATA_TYPE, DATA_NOISE)
# データを「訓練用」と「精度検証用」を指定の比率で分割し、さらにそれぞれを「データ(X)」と「教師ラベル(y)」に分ける
X_train, y_train, X_valid, y_valid = pg.split_data(data_list, training_size=TRAINING_DATA_RATIO)
# データ分割後の各変数の内容例として、それぞれ5件ずつ出力
print('X_train:'); print(X_train[:5])
print('y_train:'); print(y_train[:5])
print('X_valid:'); print(X_valid[:5])
print('y_valid:'); print(y_valid[:5])
データセットとデータローダーの作成
あとは、リスト5-1で作成した、
- X_train: 訓練用のデータ(X:行列)
- y_train: 訓練用の教師ラベル(y:ベクトル)
- X_valid: 精度検証用のデータ
- y_valid: 精度検証用の教師ラベル
のデータを使っていけばよいのだが、PyTorchで使うにはテンソルに変換する必要がある。
さらに、一般的なディープラーニングであれば、ミニバッチ学習を行うだろう。ミニバッチ学習を手動で書くこともできるが、PyTorchが提供するDataLoaderクラスを使えば簡単に実現できるので、今回はこれを利用しよう。
実際に利用するには、既存の「データ」や「教師ラベル」といったテンソルを1つのTensorDatasetオブジェクトにまとめておき、それをDataLoaderオブジェクトの生成時に指定する必要がある。なお、DataLoader/TensorDatasetはいずれも、torch.utils.dataパッケージに含まれているクラスである。
リスト5-2は、訓練用と精度検証用(=評価用)のDataLoaderオブジェクトを作成しているコードである。
# データ関連のユーティリティクラスをインポート
from torch.utils.data import TensorDataset, DataLoader
import torch # ライブラリ「PyTorch」のtorchパッケージをインポート
# 定数(学習方法設計時に必要となるもの)
BATCH_SIZE = 15 # バッチサイズ: 15(Playgroundの選択肢は「1」〜「30」)
# NumPy多次元配列からテンソルに変換し、データ型はfloatに変換する
t_X_train = torch.from_numpy(X_train).float()
t_y_train = torch.from_numpy(y_train).float()
t_X_valid = torch.from_numpy(X_valid).float()
t_y_valid = torch.from_numpy(y_valid).float()
# 「データ(X)」と「教師ラベル(y)」を、1つの「データセット(dataset)」にまとめる
dataset_train = TensorDataset(t_X_train, t_y_train) # 訓練用
dataset_valid = TensorDataset(t_X_valid, t_y_valid) # 精度検証用
# ミニバッチを扱うための「データローダー(loader)」(訓練用と精度検証用)を作成
loader_train = DataLoader(dataset_train, batch_size=BATCH_SIZE, shuffle=True)
loader_valid = DataLoader(dataset_valid, batch_size=BATCH_SIZE)
TensorDatasetクラスのコンストラクター引数には、「データ」と「教師ラベル」のテンソルをセットで指定してまとめている。
DataLoaderクラスのコンストラクター引数には、そのTensorDatasetオブジェクトと、batch_size、shuffleを指定している。
引数batch_sizeには、定数として定義したBATCH_SIZE(バッチサイズ)を指定している。そもそもバッチサイズは、「学習時」に扱うデータ単位である。しかし、DataLoaderが「ミニバッチ」に関係するため、「データ準備の段階」で定義しておく必要がある。注意してほしい。
引数shuffleには、(エポックのループが回るたびに)データをシャッフルするか(True)しないか(False)を指定する(※デフォルト値はFalse)。ミニバッチ学習ではシャッフルするのが一般的なので、今回も学習データに対して「シャッフル(True)」を指定している。
(6)ディープニューラルネットのモデル定義
以上でデータが用意できたので、ニューラルネットワークのモデル定義に取りかかりたい。その前に、今回はモデルからの出力結果(確率値)を、
- -1.0=オレンジ色
- 1.0=青色
のどちらに分類するかを決定してから、「その分類結果(予測値)と教師ラベル(正解値)が一致するかどうか(正解率)」を調べることになる。よって事前に、その分類決定の処理を実装しておきたい。
「1」か「-1」に分類するための「出力の離散化」
そこで、例えば「-0.526」や「0.923」などの確率値(probability value)が、0.0未満なら「-1.0」、0.0以上なら「1.0」といった2クラス分類値(binary classification value)に離散化(discretize)するための関数を作成することにしよう。その関数において、0.0未満とおよび0.0以上は、離散化の基点となる閾値(threshold)となる。
その関数のコードがリスト6-1である。この処理は、ニューラルネットワークの本質とは全く関係がないので、読み飛ばしてもらっても構わない(※読んでもコメントを多く入れているので難しくはないだろう)。独自関数discretizeの定義を見ると、実際の処理はthresholdの行〜returnの行のたった3行である。discretize関数は後述の「リスト7-3 1回分の「訓練(学習)」と「評価」の処理」で使用する。
import torch # ライブラリ「PyTorch」のtorchパッケージをインポート
import torch.nn as nn # 「ニューラルネットワーク」モジュールの別名定義
# 離散化を行う関数
def discretize(proba):
'''
実数の確率値を「1」か「-1」の2クラス分類値に離散化する。
閾値は「0.0以上」か「未満」か。データ型は「torch.float」を想定。
Examples:
>>> proba = torch.tensor([-0.5, 0.0, 0.5], dtype=torch.float)
>>> binary = discretize(proba)
'''
threshold = torch.Tensor([0.0]) # -1か1かを分ける閾値を作成
discretized = (proba >= threshold).float() # 閾値未満で0、以上で1に変換
return discretized * 2 - 1.0 # 2倍して-1.0することで、0/1を-1.0/1.0にスケール変換
# discretize関数をモデルで簡単に使用できるようにするため、
# PyTorchの「torch.nn.Module」を継承したクラスラッパーも作成した
class Discretize(nn.Module):
'''
実数の確率値を「1」か「-1」の2クラス分類値に離散化する。
閾値は「0.0以上」か「未満」か。データ型は「torch.float」を想定。
Examples:
>>> d = Discretize()
>>> proba = torch.tensor([-0.5, 0.0, 0.5], dtype=torch.float)
>>> binary = d(proba)
'''
def __init__(self):
super().__init__()
# forward()メソッドは、基本クラス「torch.nn.Module」の__call__メソッドからも呼び出されるため、
# Discretizeオブジェクトを関数のように使える(例えば上記の「d(proba)」)
def forward(self, proba):
return discretize(proba) # 上記の関数を呼び出すだけ
# 関数の利用をテスト
proba = torch.tensor([-0.5, 0.0, 0.5], dtype=torch.float) # 確率値の例
binary = discretize(proba) # 2クラス分類(binary classification)値に離散化
binary # tensor([-1., 1., 1.]) …… などと表示される
リスト6-1ではさらに、モデル内で扱いやすいようにtorch.nn.Module化も行っている(※ただし本連載では使用しない。あくまで実装参考用である)。
ディープニューラルネットワークのモデル設計
さていよいよモデル設計である。リスト6-2を見ると、第1回で掲載したリスト1-1(層が1つ)から、「隠れ層:2+出力層:1」の3層(※「入力層」をカウントすると4層)に拡張されて、
- 入力の数(INPUT_FEATURES): Χ1とΧ2で2つ
- 隠れ層のレイヤー数: 2つ
隠れ層にある1つ目のニューロンの数(LAYER1_NEURONS): 3つ
隠れ層にある2つ目のニューロンの数(LAYER2_NEURONS): 3つ - 出力層にあるニューロンの数(OUTPUT_RESULTS): 1つ
というモデル設計になっていることが分かるだろう。リスト6-2の太字は、第1回のリスト1-1から追記/変更により変わった部分である。
import torch # ライブラリ「PyTorch」のtorchパッケージをインポート
import torch.nn as nn # 「ニューラルネットワーク」モジュールの別名定義
# 定数(モデル定義時に必要となるもの)
INPUT_FEATURES = 2 # 入力(特徴)の数: 2
LAYER1_NEURONS = 3 # ニューロンの数: 3
LAYER2_NEURONS = 3 # ニューロンの数: 3
OUTPUT_RESULTS = 1 # 出力結果の数: 1
# 変数(モデル定義時に必要となるもの)
activation1 = torch.nn.Tanh() # 活性化関数(隠れ層用): tanh関数(変更可能)
activation2 = torch.nn.Tanh() # 活性化関数(隠れ層用): tanh関数(変更可能)
acti_out = torch.nn.Tanh() # 活性化関数(出力層用): tanh関数(固定)
# torch.nn.Moduleによるモデルの定義
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
# 隠れ層:1つ目のレイヤー(layer)
self.layer1 = nn.Linear(
INPUT_FEATURES, # 入力ユニット数(=入力層)
LAYER1_NEURONS) # 次のレイヤーの出力ユニット数
# 隠れ層:2つ目のレイヤー(layer)
self.layer2 = nn.Linear(
LAYER1_NEURONS, # 入力ユニット数
LAYER2_NEURONS) # 次のレイヤーへの出力ユニット数
# 出力層
self.layer_out = nn.Linear(
LAYER2_NEURONS, # 入力ユニット数
OUTPUT_RESULTS) # 出力結果への出力ユニット数
def forward(self, x):
# フォワードパスを定義
# 「出力=活性化関数(第n層(入力))」の形式で記述する
x = activation1(self.layer1(x)) # 活性化関数は変数として定義
x = activation2(self.layer2(x)) # 同上
x = acti_out(self.layer_out(x)) # ※活性化関数は「tanh」固定
return x
# モデル(NeuralNetworkクラス)のインスタンス化
model = NeuralNetwork()
model # モデルの内容を出力
注意点/ポイントとしては、例えば定数「LAYER1_NEURONS」に着目すると、この定数は1つ目のレイヤーにおける「出力ユニット数」であり、かつ2つ目のレイヤーの「入力ユニット数」でもあるという点、つまり「全く同じものが指定されている」という点が大切である。「前の層の出力(=ニューロンの数)」と「次の層の入力」の数は、このように正しく一致させる必要がある。
また、フォワードプロパゲーション(順伝播)時のデータ(x)が変換されていく流れは、forwardメソッド内に分かりやすく定義されている点にも着目してほしい。最初の入力(x)が1つ目のレイヤーを通り、活性化関数(activation1)で変換されて、出力(x)される。その出力値(x)が同様に2つ目のレイヤーを……と流れていくのが分かるだろう。
(7)学習/最適化(オプティマイザ)
いよいよ大詰め。「学習/最適化」を実装していこう。
Copyright© Digital Advantage Corp. All Rights Reserved.