検索
連載

第3回　PyTorchによるディープラーニング実装手順の基本：PyTorch入門（2/2 ページ）

いよいよ、PyTorchを使ったディープラーニングの流れを通して全体的に説明する。ミニバッチ学習を手軽にするデータローダーから始めて、ディープニューラルネットワークのモデル定義、オプティマイザを使った学習、損失／正解率の出力やグラフ表示といった評価までを解説。

[一色政彦，デジタルアドバンテージ] PC用表示 関連情報
Share
Tweet
LINE
Hatena
前のページへ | 　　　　　　

（7）学習／最適化（オプティマイザ）

　いよいよ大詰め。「学習／最適化」を実装していこう。

オプティマイザ（最適化用オブジェクト）の作成

　学習を行う最適化アルゴリズム（Optimizer：オプティマイザ）は、自分で実装する必要はなく、PyTorchに用意されているクラスをインスタンス化するだけである（※もちろん必要に応じて自分で実装することも可能）。リスト7-1はその例で、「SGD」（Stochastic Gradient Descent： 確率的勾配降下法）用のクラスを使っている。

import torch.optim as optim   # 「最適化」モジュールの別名定義

# 定数（学習方法設計時に必要となるもの）
LEARNING_RATE = 0.03   # 学習率： 0.03
REGULARIZATION = 0.03  # 正則化率： 0.03

# オプティマイザを作成（パラメーターと学習率も指定）
optimizer = optim.SGD(           # 最適化アルゴリズムに「SGD」を選択
    model.parameters(),          # 最適化で更新対象のパラメーター（重みやバイアス）
    lr=LEARNING_RATE,            # 更新時の学習率
    weight_decay=REGULARIZATION) # L2正則化（※不要な場合は0か省略）

リスト7-1　オプティマイザ（最適化用オブジェクト）の作成

　torch.optim.SGDクラスのコンストラクターには、

  • パラメーター： 重みやバイアスのこと。第1回で説明した通り、＜モデル名＞.parameters()メソッドで取得できる
  • 引数lr： 学習率。この例では定数LEARNING_RATEとして定義している
  • 引数weight_decay： 正則化率。正則化（Regularization）は「L2」（＝重み減衰： Weight Decay）に相当する（※あまり使わない「L1」はPyTorchによる最適化アルゴリズムの基本機能には含まれていない）

を指定する。正則化が不要な場合は、引数weight_decayを省略してもよい。

　PyTorchでは、「オプティマイザ」のクラスとしてtorch.optimパッケージ内に以下のものが用意されており、すぐに利用できる（※カッコ書きがあるものは特に有名なもの）。

  • Adadelta
  • Adagrad（有名）
  • Adam（有名）
  • AdamW
  • SparseAdam
  • Adamax
  • ASGD
  • LBFGS
  • RMSprop（有名）
  • Rprop
  • SGD（確率的勾配降下法）

損失関数の定義

　次に、バックプロパゲーションで必要となる損失関数（Loss Function）を定義する。これも自分で実装する必要は（基本的に）なく、PyTorchに用意されているクラスをインスタンス化するだけである。リスト7-2はその例で、「MSE」（Mean Squared Error： 平均二乗誤差）用のクラスを使っている。

# 変数（学習方法設計時に必要となるもの）
criterion = nn.MSELoss()  # 損失関数：平均二乗誤差

リスト7-2　損失関数の定義

　第1回で説明した通り、「損失関数」クラスのインスタンスが代入される変数の名前は、慣例でcriterionとする。この名前は、誤差からの損失を測る「基準（criterion）」を意味する。

　PyTorchでは、「損失関数」のクラスとしてtorch.nnパッケージ内に以下のものが用意されており、すぐに利用できる（※カッコ書きがあるものは特に有名なもの）。

  • L1Loss（MAE：Mean Absolute Error、平均絶対誤差）
  • MSELoss（平均二乗誤差）
  • CrossEntropyLoss（交差エントロピー誤差： クラス分類）
  • CTCLoss
  • NLLLoss
  • PoissonNLLLoss
  • KLDivLoss
  • BCELoss
  • BCEWithLogitsLoss
  • MarginRankingLoss
  • HingeEmbeddingLoss
  • MultiLabelMarginLoss
  • SmoothL1Loss
  • SoftMarginLoss
  • MultiLabelSoftMarginLoss
  • CosineEmbeddingLoss
  • MultiMarginLoss
  • TripletMarginLoss

1回分の「訓練（学習）」と「評価」の処理

　それでは、最重要ポイントであるバックプロパゲーション（Back-propagation：Backprop、誤差逆伝播）を行う。これは、第1回の「リスト3-2　ニューラルネットワークにおける各パラメーターの勾配」で示したように、損失（loss）オブジェクトのbackward()メソッドを呼び出すだけである。

　その損失（loss）オブジェクト自体は、先ほどインスタンス化した「損失関数」オブジェクト（criterion）を関数のように呼び出すと得られる。この関数の引数に、モデルの出力結果（pred_y）と正解ラベル（train_y）を指定することは、第1回の「リスト3-2」と同じである。

　バックプロパゲーションを行った後は、最適化（Optimization）の処理として、計算された微分係数（＝勾配）でパラメーター（重みとバイアス）を更新していく必要がある。この作業は手動で書くこともできるが、オプティマイザ（optimizer）を使えばstep()メソッドを呼び出すだけで実現できるので便利だ。

　なお、勾配はbackward()メソッドを呼び出すたびに蓄積する仕様なので、backward()メソッドを呼び出す前に、optimizer.zero_grad()メソッドを呼び出すことで勾配を毎回、0にリセットする必要があることに注意してほしい（※もしくはoptimizer.step()メソッドを呼び出した後でリセットしてもよい）。この処理は重要なわりに特に忘れやすいので要注意である。もしoptimizer.zero_grad()を書き忘れると、勾配が累積してしまい正しい計算結果ではなくなってしまう。

　以上の一連の訓練（学習）処理を実装したのが、リスト7-3のtrain_step関数である。また、評価（精度検証）用として、バックプロパゲーション以降の処理を行わずに損失だけを取得する処理を実装したのがvalid_step関数である。リスト7-3の太字は、第1回のリスト3-2から追記／変更により変わった部分である。

def train_step(train_X, train_y):
    # 訓練モードに設定
    model.train()

    # フォワードプロパゲーションで出力結果を取得
    #train_X                # 入力データ
    pred_y = model(train_X) # 出力結果
    #train_y                # 正解ラベル

    # 出力結果と正解ラベルから損失を計算し、勾配を求める
    optimizer.zero_grad()   # 勾配を0で初期化（※累積してしまうため要注意）
    loss = criterion(pred_y, train_y)     # 誤差（出力結果と正解ラベルの差）から損失を取得
    loss.backward()   # 逆伝播の処理として勾配を計算（自動微分）

    # 勾配を使ってパラメーター（重みとバイアス）を更新
    optimizer.step()  # 指定されたデータ分の最適化を実施

    # 正解数を算出
    with torch.no_grad(): # 勾配は計算しないモードにする
        discr_y = discretize(pred_y)         # 確率値から「-1」／「1」に変換
        acc = (discr_y == train_y).sum()     # 正解数を計算する

    # 損失と正解数をタプルで返す
    return (loss.item(), acc.item())  # ※item()=Pythonの数値

def valid_step(valid_X, valid_y):
    # 評価モードに設定（※dropoutなどの挙動が評価用になる）
    model.eval()
    
    # フォワードプロパゲーションで出力結果を取得
    #valid_X                # 入力データ
    pred_y = model(valid_X) # 出力結果
    #valid_y                # 正解ラベル

    # 出力結果と正解ラベルから損失を計算
    loss = criterion(pred_y, valid_y)     # 誤差（出力結果と正解ラベルの差）から損失を取得
    # ※評価時は勾配を計算しない

    # 正解数を算出
    with torch.no_grad(): # 勾配は計算しないモードにする
        discr_y = discretize(pred_y)     # 確率値から「-1」／「1」に変換
        acc = (discr_y == valid_y).sum() # 正解数を合計する

    # 損失と正解数をタプルで返す
    return (loss.item(), acc.item())  # ※item()=Pythonの数値

リスト7-3　1回分の「訓練（学習）」と「評価」の処理

　train_step関数／valid_step関数の冒頭では、model.train()／ model.eval()メソッドが呼び出されている。これは訓練モード／評価（推論）モードを切り替えるためのものだ。通常は、訓練モードになっているが、評価モードに切り替えると、（今回は使っていないが）BatchNorm（バッチ正規化）やDropout（ドロップアウト）などの挙動が評価用になる。

　先ほどバックプロパゲーションから最適化までの訓練処理を説明したが、その後に「正解数の算出」という処理がそれぞれのメソッドにある。これは、後ほど説明する「リスト7-4」で学習によって正解率が変化してく様子を出力するために計算している。最後のreturnによって、計算済みの「損失」と「正解数」をタプルでまとめて、関数の呼び出し元に返却している。呼び出し元では、この2つの数値を使って、損失や正解率の推移を出力したりグラフ化したりできる。

　この「正解数の算出」処理の内容を詳しく見ると、with torch.no_grad():というコードで始まっている。この配下のテンソル計算のコードには、「自動微分」用の勾配が生成されなくなり、メモリ使用量軽減やスピードアップなどの効果が見込める。

　さらに、正解かどうかを判断するために、前掲の『リスト6-1　「1」か「-1」に分類するための「出力の離散化」』で説明したdiscretize関数が使われている。

「訓練」と「評価」をバッチサイズ単位でエポック回繰り返す

　以上で、バックプロパゲーション＆最適化の実装も完了した。あとは、自分で指定したエポック数だけtrain_step関数とvalid_step関数を呼び出すだけである。この処理には、forループを使えばよい。

　また、今回のようにミニバッチ学習をする場合は、エポック数のforループの中に、ミニバッチ単位のforループを作り、その中でtrain_step関数とvalid_step関数を呼び出す必要がある。

　ミニバッチ単位のforループが難しそうに感じるが、リスト5-2で作成しておいたDataLoaderオブジェクトがここで役に立つ。先ほど、訓練用／精度検証用のオブジェクトをloader_train／loader_valid変数に格納している。

　以上の2つのforループを実装しているのがリスト7-4のコードである。その中で、訓練用のtrain_step関数や、評価用のvalid_step関数が呼び出されているのを確認してほしい。なおforループの中では、たくさんの変数が使われておりコードが長くなってしまっているが、どれも表示用の損失や正解率を計算するための処理であり、ニューラルネットワークの本質ではないので、ざっと眺めるだけでよい。リスト7-4の太字は、forループとtrain_step／valid_step関数の呼び出し、さらに後述するパラメーター初期化に関する部分である。

# パラメーター（重みやバイアス）の初期化を行う関数の定義
def init_parameters(layer):
    if type(layer) == nn.Linear:
        nn.init.xavier_uniform_(layer.weight) # 重みを「一様分布のランダム値」に初期化
        layer.bias.data.fill_(0.0)            # バイアスを「0」に初期化

# 学習の前にパラメーター（重みやバイアス）を初期化する
model.apply(init_parameters)

# 定数（学習／評価時に必要となるもの）
EPOCHS = 100             # エポック数： 100

# 変数（学習／評価時に必要となるもの）
avg_loss = 0.0           # 「訓練」用の平均「損失値」
avg_acc = 0.0            # 「訓練」用の平均「正解率」
avg_val_loss = 0.0       # 「評価」用の平均「損失値」
avg_val_acc = 0.0        # 「評価」用の平均「正解率」

# 損失の履歴を保存するための変数
train_history = []
valid_history = []

for epoch in range(EPOCHS):
    # forループ内で使う変数と、エポックごとの値リセット
    total_loss = 0.0     # 「訓練」時における累計「損失値」
    total_acc = 0.0      # 「訓練」時における累計「正解数」
    total_val_loss = 0.0 # 「評価」時における累計「損失値」
    total_val_acc = 0.0  # 「評価」時における累計「正解数」
    total_train = 0      # 「訓練」時における累計「データ数」
    total_valid = 0      # 「評価」時における累計「データ数」

    for train_X, train_y in loader_train:
        # 【重要】1ミニバッチ分の「訓練」を実行
        loss, acc = train_step(train_X, train_y)

        # 取得した損失値と正解率を累計値側に足していく
        total_loss += loss          # 訓練用の累計損失値
        total_acc += acc            # 訓練用の累計正解数
        total_train += len(train_y) # 訓練データの累計数
            
    for valid_X, valid_y in loader_valid:
        # 【重要】1ミニバッチ分の「評価（精度検証）」を実行
        val_loss, val_acc = valid_step(valid_X, valid_y)

        # 取得した損失値と正解率を累計値側に足していく
        total_val_loss += val_loss  # 評価用の累計損失値
        total_val_acc += val_acc    # 評価用の累計正解数
        total_valid += len(valid_y) # 訓練データの累計数

    # ミニバッチ単位で累計してきた損失値や正解率の平均を取る
    n = epoch + 1                             # 処理済みのエポック数
    avg_loss = total_loss / n                 # 訓練用の平均損失値
    avg_acc = total_acc / total_train         # 訓練用の平均正解率
    avg_val_loss = total_val_loss / n         # 訓練用の平均損失値
    avg_val_acc = total_val_acc / total_valid # 訓練用の平均正解率

    # グラフ描画のために損失の履歴を保存する
    train_history.append(avg_loss)
    valid_history.append(avg_val_loss)

    # 損失や正解率などの情報を表示
    print(f'[Epoch {epoch+1:3d}/{EPOCHS:3d}]' \
          f' loss: {avg_loss:.5f}, acc: {avg_acc:.5f}' \
          f' val_loss: {avg_val_loss:.5f}, val_acc: {avg_val_acc:.5f}')

print('Finished Training')
print(model.state_dict())  # 学習後のパラメーターの情報を表示

リスト7-4　「訓練」と「評価」をバッチサイズ単位でエポック回繰り返す

　コードの冒頭でmodel.apply(init_parameters)関数により、パラメーターの初期化を行っている。これは、第1回の「パラメーター（重みとバイアス）の初期値設定」の節で触れた処理である。

　独自に定義しているinit_parameters関数の内容も簡単に説明しておくと、レイヤー（層）の種類が「nn.Linear」（全結合層）である場合には、重みをnn.init.xavier_uniform_()関数により「一様分布のランダム値」に初期化、バイアスをlayer.bias.data.fill_(0.0)メソッドにより「0」に初期化する仕様のコードとなっている。※どちらも「*_()」パターンの関数なので（第2回で説明）、現在の重み／バイアス自体の値が変更されることになる。

　ちなみに、早期終了（Early Stopping、早期停止）はオプティマイザの基本機能に含まれていないので今回は説明しない（実装のヒントとしては、損失が変化しなくなっている様子を捉えて処理を中断させるコードを足せばよい）。

（8）評価／精度検証

　リスト7-4には評価のコードも含まれているので、以上のコードだけで評価までが行える。

損失値と正解率の出力

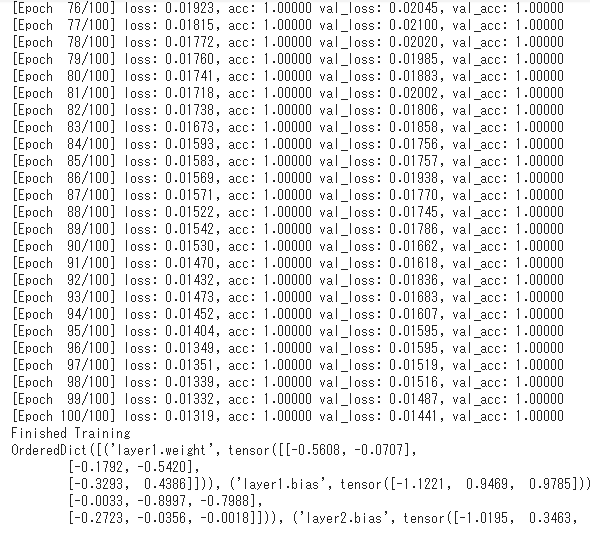
　実際に、リスト7-4を実行してみたのが図8-1である。

図8-1　シンプルな座標点データ（分類用の円）
図8-1　シンプルな座標点データ（分類用の円）

　エポックのループが回るたびに、

  • [Epoch ＜現在のエポック番号＞/＜エポック数＞]
  • loss: ＜訓練の損失値＞
  • acc: ＜訓練の正解率＞
  • val_loss: ＜精度検証の損失値＞
  • val_acc: ＜精度検証の正解率＞

が出力されている。この画像では、正解率は100％に達してしまっているが、最初の方ではループが回るたびに数％ずつ正解率が上がっていく様子が見られた。

　リスト7-4の最後でmodel.state_dict()メソッドを呼び出しているので、パラメーター（重みやバイアス）などのモデル（＝torch.nn.Module派生クラスのインスタンス）全体の状態も出力されている。

損失値の推移グラフ描画

　最後に、テキストの出力だけでなく、視覚的なグラフでも結果を確認する方法を示しておこう。

　前掲のリスト7-4をよく見ると、エポックのループが回るたびに、train_history／valid_history変数に訓練時／評価時の損失値をリストに追加していた。そのリスト値（＝損失の履歴）をグラフ描画ライブラリ「Matplotlib」に食わせるだけである（リスト8-1）。

import matplotlib.pyplot as plt

# 学習結果（損失）のグラフを描画
epochs = len(train_history)
plt.plot(range(epochs), train_history, marker='.', label='loss (Training data)')
plt.plot(range(epochs), valid_history, marker='.', label='loss (Validation data)')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

リスト8-1　損失値の推移グラフ描画

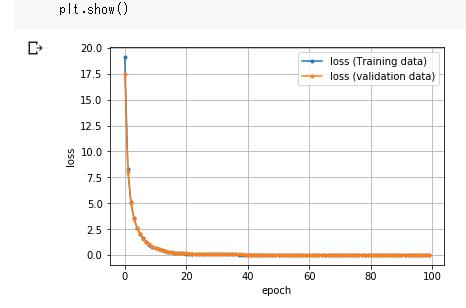
　このグラフのプロット方法はいたって普通なので（※ちなみに第1回で紹介した連載記事「後編： ディープラーニング最速入門」の「リスト7-1　損失値の推移グラフ描画」がほぼ同じコードである）、本連載では説明を割愛する。リスト8-1を実行すると、図8-2の画像が出力された。

図8-2　損失値の推移グラフの例
図8-2　損失値の推移グラフの例

まとめ

　以上でPyTorchによるニューラルネットワークの基本を一通り学んだことになる。今回の知識を武器に、ぜひPyTorchを使いこなしてほしい。

　今後も、本連載にPyTorchの活用方法の記事を追加していく予定である。

「PyTorch入門」のインデックス

「PyTorch入門」

Copyright© Digital Advantage Corp. All Rights Reserved.

前のページへ | 　　　　　　
[an error occurred while processing this directive]
ページトップに戻る