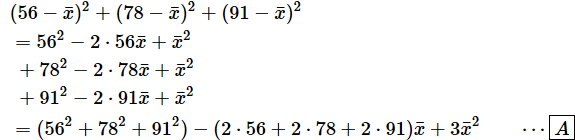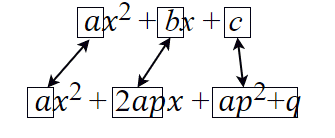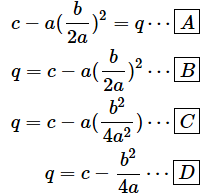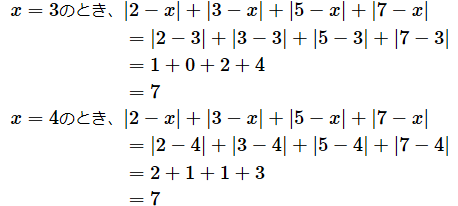[AI・機械学習の数学]文字式を使いこなせば一気にレベルアップ:AI・機械学習の数学入門(3/3 ページ)
数字(1、2、3、……)の式の次は、文字(a、b、x、y、……)を使った式をおさらいしよう。これまでに学んだ知識と平方完成を使って、距離の二乗和の最小値を求める計算も行う。
解説:添字の利用
高校に入ると扱うデータの数や種類も増えてきます。しかし、アルファベットは26文字しかないので、100人のデータの平均を取るといった場合には、aとかbといった英字だけではうまく書けません。そこで、x1やx2といった書き方で各データを表します。こう書けば、同じ種類の値が幾つかあって、それらを番号で区別したいときに便利です。学生1、学生2、学生3のように番号で区別するのと同じです。
例えば、x1とx2とx3の平均値を求めるなら、
となります。この小さな1とか2とか3のことを「添字(そえじ)」と呼びます*4。x1の読み方は「エックスいち」です。場合によっては「エックスのいち」とか「エックスのいちばん」ということもあるかもしれません。もちろん、小さな字だからといって小さな声で読むなどという必要はありません(そんなことをする人はいないでしょうが)。なお、個々のデータのことを「要素」ということもあります。
添字を使えば、データがたくさんあっても1つの文字で複数の値が区別できますね。100人のデータの平均を求めるなら、以下のように表せます。
また、n人のデータの平均を求めるなら、以下のように表せます。
ここで、添字にも文字を使って表していることに注目してください。xnなら、xのn番目という意味になります。nは一般にデータの個数を表すのに使うことが多いので、最後の値(xn)ではなく「何番目か」の値を表したいときにはiやjなどを添字に使って表すのが一般的です。例えば、
のように書きます。iの値を変えれば好きな要素が指定できるというわけです。
ところで、n人の平均値を求める式の分子の方を見て何か気が付かないでしょうか。式を見ているだけだと気にならないかもしれませんが、この式を書け、と言われるとどうでしょう。いちいちx1+x2+ ... + xnと書くのはとても面倒ですね。1番のデータからn番のデータまでを合計するという決まり切った計算なので、もっと簡単に書きたいものです。
そこでいよいよ、Σ(シグマ)の登場です……と進みたいところなのですが、お話がかなり長くなってきたので、一応、予告だけということにして、詳しい説明は次回のお楽しみということにしましょう。
Σ、総和、つまり「全部足す」ということを表す記号ですが、機械学習のための計算でよく登場します。式の左辺は、Σが「全て足す」、下のi=1は「iの値は1から始める」、上のnは「iの値はnまで」、右のxiは、「xiを」ということになります。右辺のように長々と書く必要がなくなりますね。詳細については、次回ということで……。
文字式と文字式の計算の基本はここまでです。ホントに最低限ではありますが、これだけで十分先に進めます。このあとは少しだけ応用的な話題を取り上げ、文字式が問題解決に役立つことを見てみましょう。
各データとの距離の2乗の総和が最小になる値とは???
ここからは、文字式の計算に慣れるための練習をかねて、機械学習で使われる計算を少しだけ掘り下げて見ていきます(※これについては、計算過程を分かりやすく解説する音声解説付き動画も用意していますので、「難しい」と感じたら、ぜひ視聴してみてください)。
動画5 距離の二乗和を求める
問題:距離の二乗和の最小値を求める
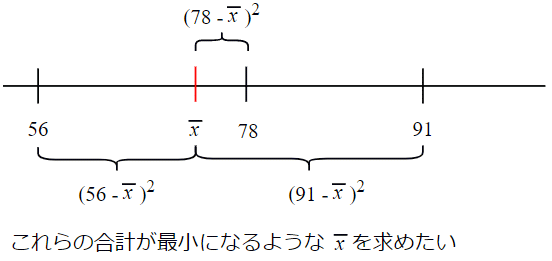
最初に56と78と91という3つの値を例として使いました。ここでは、これらの値と数直線上での距離の2乗の総和(二乗和と略します)が最も小さくなる点を見つける計算をしてみましょう。つまり、以下の図5のような点を求めるというわけです。
xの上に ̄が付いていますが、これはまあ飾りのようなものです。今は、あまり気にしないでください(読み方は「エックス・バー」です)。意味はあとで説明しますが、見慣れない記号にちょっと免疫を付けるためにお見せしたといった程度に考えておいてもらってけっこうです。
仮にその求める値を
としましょう。まず、距離の二乗和を求めてみます。
距離の二乗和を求める
前回見たように、引き算をして2乗するのでしたね。つまり、
この式の下線の部分は、
の形になっています。+と−の違いがありますが、bを引くのではなく、−bを足すと考えれば公式が適用できます。
- [A] …… −bを+(−b)と考えて、公式を適用した
- [B] …… (−b)2=b2なので、こうなる。この公式を利用すればよい
では、これを使って、問題となる式を展開してみましょう。
- [A] …… 同類項をまとめた
562とか2 ⋅ 56の計算は、何も暗算や筆算でやらなくても電卓を使えばいいですね。計算してまとめると、
となります(※ここまでの計算が難しいと感じたら、前掲の解説動画【距離の二乗和の最小値を求める】をご視聴ください)。
この式はどこかで見たことがある式ですね。そう、
という二次関数の右辺です。項の順序を、
の次数が高い方から(降べきの順に)整理して、y=を付けると、
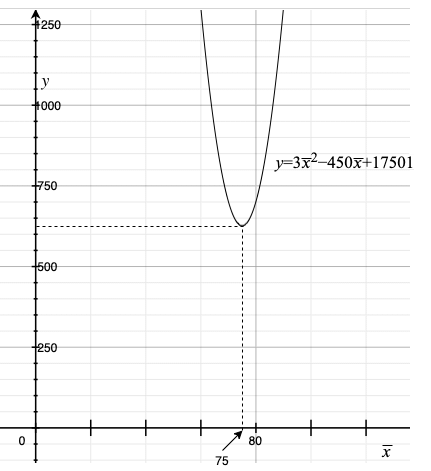
となります。そこで、このグラフを描いてみましょう。
の係数が正であれば、下に凸なグラフになりますね(図6)。かなり縦長になるので、横幅を拡大して見やすくしてあります*5。
*5 このグラフはmacOSに付属しているGrapherというアプリで描いたものです。数式を使ったグラフの描画にはWolframAlphaやGeoGebraなどのサイトやそれらのアプリも便利です。
縦軸がyつまり、
の値です。グラフを見ると、この式の値が最小になる点があることが分かります。そのときの
の値はいくらかというと75です。75というと……なんと、56と78と91の平均値ではありませんか! 私たちがグラフから見つけた値は、各データとの距離の二乗和が最小になる値でしたよね。つまり、平均値とは各データとの距離の二乗和が最小になる値だったのです。
最初、
という表記のことをむにゃむにゃとごまかしていましたが、データ(xi)から求めた平均値を、一般に
と表します(最初にそれを言ってしまうとネタバレになるので、さらっと流したというわけです)。今後は、
と書いてあれば、ああ、平均値なんだな、ということがひと目で分かるようになりましたね。
ところで、この75という値をグラフから読み取るのではなく、計算できちんと求めたいですよね。そんなもの、平均値なんだから全部足して個数で割ればいいじゃないか、と言われるかもしれませんが、それは結果としてそうなるだけのことです。そうではなく、各データとの距離の総和が最小になる値を計算で求めて、それが確かに平均値になっていることを確かめようというわけです。
最小値を求めるために式を変形する(平方完成)
(※ここから本章の最後までに説明する「平方完成」の計算過程は動画でも分かりやすく説明しています。文章を読んで「難しい」と感じたら、ぜひ視してみてください。)
動画6 二次式の最小値を求める(平方完成)
高校の数学を少し覚えていれば、下に凸な二次関数
の値を最小とする
を求めるなら「微分して0と置く、だろ」と思われる方もいると思います。まさにその通りですし、その方が計算ははるかに簡単なのですが、文字式にもう少し慣れるために、ここはあえて微分を使わずにやってみましょう。実は中学校までの数学でできます*6。
私たちがやりたいのは、
という式の値を最小にする
の値を見つけるということでした。まず、この式の形に注目しましょう。この式は、
と同じ形になっていますね。a、b、cを指さし確認してみましょう! 答えは(※オレンジ色の部分をそれぞれクリックまたはタップすると表示されます)、
- (1)式の 3 が、aに当たり
- (1)式の -450 が、bに当たり
- (1)式の 17502 が、cに当たります
さて、最小値を求めるために、この式を以下のような形に変形してみたいと思います(この変形のことを平方完成と呼びます)。
このとき、(x+p)2は、2乗されているので必ず0以上になることに注目してください。qの値は決まっていますから、aの値が正であれば(グラフが下に凸であれば)、全体が最小になるのは(x+p)2が0のとき、つまりx=(−p)のときです(図7)。
数学の教科書や授業では、ax2 + bx + cを割ったり掛けたり足したり引いたりしてa(x + p)2 + qの形に変形するのですが、ここでは思いっきり楽をしましょう。登山道で言えば、上級者向けコースを登るのではなく、初心者向けコースを降りてくる感じです。その分、ちょっと説明は長くなりますが、なだらかな道です(上級者向けの簡潔な変形も動画には含めてあります。興味がある方は後掲の動画【二次式から平方完成の式に変形する別の方法(上級者向け)】を視聴してください)。
というわけで、平方完成の逆のコースをたどり、a(x + p)2 + qをax2 + bx + cの形にすればどうなるかを見ていくことにします。まずは、かっこの展開からです。
- [A] …… (a+b)2 = a2+2ab+b2という公式を使った(二次式の展開)
- [B] …… a(x+y) = ax+ayという公式を使った(分配法則)
これと、ax2 + bx + cを比較してみます。以下の図8のように、aはそのままaに対応していますが、b=2ap、c=ap2+qです。
ここで、以下の連立方程式が得られました。
平方完成した式のpについて解く(連立方程式)
おっと、いきなり連立方程式ですか! とビビってしまう方もおられると思いますが、一歩ずつ丁寧に見ていけば怖れることはありません。まず、(1)の両辺を2aで割っても左辺と右辺が等しいことに変わりはありませんね。従って、
となります。つまり、
であることが分かりました(a>0なので、aは0ではありません。従って割り算ができます)。実は、xの最小値を求めるだけなら、これですでに答が求められています。図7で示したように、xの値が−pのとき、つまり、xの値が、
のときです。が、せっかくなので、これ以降の計算もついでにやっておきます(※計算はもううんざり、という人は「ゴール:最小値を求める」まで読み飛ばしてもらっても構いません)。
平方完成した式のqについて解く(連立方程式)
次に、(3)式を(2)式のpに代入しましょう。
のだから、pの部分を、
に書き替えても式は成り立ちますね。
となります。従って、
これで、pとqが求められました。
に当てはめてみましょう。
ゴール:最小値を求める
ところで、私たちが関心を持っているのは、この式を最小にするxの値です。それは、アンダーラインを引いた部分から、
であることが分かります。そこで、
に戻ると、
なので、
できました! 式の値、つまり、各データとの距離の二乗和が最小になる
の値が計算で75と求められました。ちゃんと平均値になっていますね。
平均値は、よく「極端に大きな値や極端に小さな値があると、それらの値に引きずられてしまう」と言われます。全部足して個数で割るという計算方法からは分かりませんが、そもそも元の値を二乗しているからなのです(例えば、大きな値を二乗すればより大きくなります)。
さて、今回のお話はこのあたりでおしまいですが、次回はΣを取りあげるので、これまでやってきた計算を一般化する(ここでは具体的な数値を使って確認しましたが、どんな値でも成り立つことを示す)、といったことにも挑戦してみたいと思います。
*余談 なぜ、各データとの距離の総和を最小にする値ではなく、距離の2乗の総和を最小にする値を求めるのか、と思われる方がいるかもしれませんね。前回は「絶対値は扱いが面倒だから」といった感じでさらっと流しましたが、距離を最小にする値が1つに決まらないことがあるというのが大きな理由です。具体例で見てみましょう。
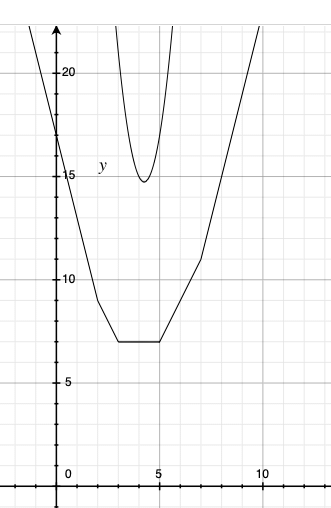
例えば、2,3,5,7というデータがあったとします。距離を最小にする値は、|2−x|+|3−x|+|5−x|+|7−x|の最小値です。距離の2乗の総和を最小にする値は(2−x)2+(3−x)2+(5−x)2+(7−x)2の最小値です。絶対値の計算はけっこう面倒なので、Grapherを使ってグラフを描いてみます。
このグラフのカクカクした方が絶対値の総和のグラフです。このことからも分かるように、距離の総和の最小値は1つだけではありません。計算してみましょう。
となります。同様に、x=5のときも、最小値は7となります(3 < x ≦ 5を満たすxであればいいので、無限にあります)。一方、2乗を最小にする値は唯一に決まります。
蛇足ですが、三角形の各頂点からの距離の和を最小にする点をフェルマー点と呼びます(フェルマーさんはよく登場しますね)。また、三角形の各頂点からの距離の2乗の和を最小にする点は重心と呼ばれます。重心は三角形のように点が3つの場合だけでなく、点が幾つあっても1つに決まります。ちなみに、重心はk-means法と呼ばれるクラスタリング(=グループ分け)のアルゴリズムなど、さまざまな手法で使われます。
(※次の動画は、前述した「平方完成の形への簡潔な変形方法(上級者向け)」を説明しています。興味がある方はご視聴ください。)
動画7 二次式から平方完成の式に変形する別の方法(上級者向け)
次回は……
多くのデータを合計するというのは平均を求める場合だけでなく、さまざまな場面で登場する計算です。次回は、全てを合計する(=総和を求める)のに使うΣという記号を取り上げます。Σを利用した計算ができるようになると、数式をより簡潔に、また正確に表せるようになり、複雑な問題をスッキリと解きほぐすのにも役立ちます。
Copyright© Digital Advantage Corp. All Rights Reserved.