連載
[活性化関数]恒等関数(Identity function)/線形関数(Linear function)とは?:AI・機械学習の用語辞典
用語「恒等関数(線形関数)」について説明。入力値と全く同じ数値を返す、ニューラルネットワークの活性化関数を指す。
用語解説
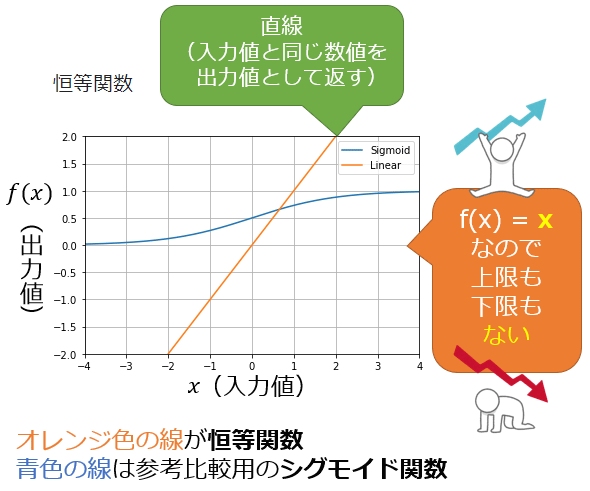
AI/機械学習のニューラルネットワークにおける恒等関数(Identity function)もしくは線形関数(Linear function)とは、あらゆる入力値を、全く同じ数値に変換して(=そのまま)出力する関数である。なお、「線形関数」(線形:リニア=直線的)と言っても、活性化関数の場合は(基本的に)入力と出力が「同じ値」となる直線を指す(図1)。
主に回帰問題における出力層の活性化関数として用いられる。主要ライブラリでは、次の関数/クラスで定義されている。
- TensorFlow(2.x)/Keras: linear()関数など
- PyTorch: Identityクラスなど
定義と数式
名前は仰々しいが、関数の中身は非常に単純だ。数式としてあらためて書き出すほどではないが、他の活性化関数の説明と体裁を統一するために書き出しておくと次のようになる。
説明不要だと思うが、この数式の導関数(Derivative function:微分係数の関数)を求めると、次のようになる。
Pythonコード
Pythonコードの説明も不要だと思うが、説明表記の統一のために書き出しておくとリスト1のようになる。
def identity(x):
return x
リスト1 恒等関数のPythonコード例
その導関数(derivative function)のPythonコードは、リスト2のようになる。
def der_identity(x):
return 1.0
リスト2 恒等関数の「導関数」のPythonコード例
Copyright© Digital Advantage Corp. All Rights Reserved.