［活性化関数］ソフトマックス関数（Softmax function）とは？：AI・機械学習の用語辞典

用語「ソフトマックス関数（Softmax function）」について説明。複数の入力値（＝ベクトルの各成分）をそれぞれ「0.0」～「1.0」の確率値に変換し、複数の出力値（＝ベクトルの各成分）の合計が常に「1.0」（＝100％）になる関数を指す。ニューラルネットワークの出力層での活性化関数として、特に多クラス分類問題で使用される。

[一色政彦，デジタルアドバンテージ] PC用表示関連情報

LINE

Hatena

連載目次

用語解説

　AI／機械学習のニューラルネットワークなどにおけるソフトマックス関数（Softmax function、もしくは正規化指数関数： Normalized exponential function）とは、入力データ（＝ベクトル）内の複数の値（＝ベクトルの各成分）を0.0～1.0の範囲の確率値に変換する関数である。この関数によって出力される複数の値（＝ベクトルの各成分）の合計は常に1.0（＝100％）になる。

　ソフトマックス関数の出力値をグラフにすると、滑らかな（＝ソフトな）曲線が得られる（図1）。この滑らかさと、1つの成分だけが最大値を取る特性から「ソフトマックス関数」と呼ばれる。

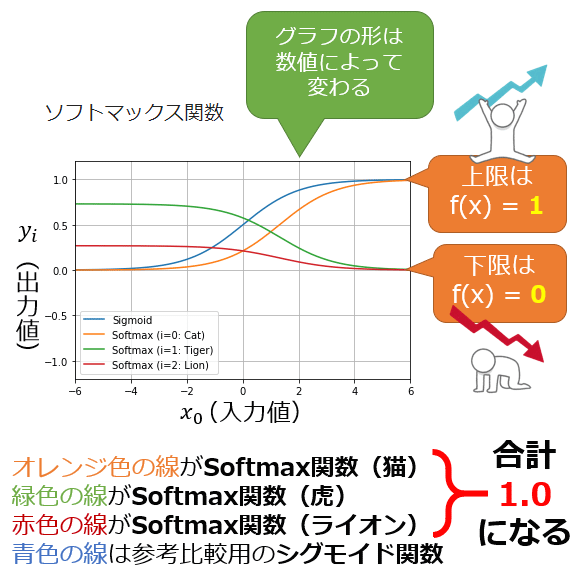
図1　「ソフトマックス関数」のグラフのイメージ
このグラフは、3つの成分を持つベクトルの1つの成分x₀を変化させた際の、ソフトマックス関数の出力を示している。具体的には、x₀（横軸）を変化させ、x₁を1.0、x₂を0.0と固定してソフトマックス関数に入力。出力は「猫」「虎」「ライオン」という3つのクラスの確率値として曲線で表現されている。また、参考のためにシグモイド関数のグラフも示している。

　例えば図1は、「猫」「虎」「ライオン」を分類する問題を仮定している。その問題を解くニューラルネットワークの出力層において、

猫（x₀、i＝0）
虎（x₁、i＝1）
ライオン（x₂、i＝2）

という3つの入力（x_i、xはベクトル）があり、それをソフトマックス関数で変換した出力結果（y_i、yはベクトル）をグラフ化したものである。例えば入力値x₀が4.0のときを見てほしい。オレンジ色の線（y₀＝猫）だけがほぼ1.0となり、それ以外の緑色の線（y₁＝虎）や赤色の線（y₂＝ライオン）はほぼ0.0となっている。※なお、この曲線は、各変数の入力値の状況などによって変わる（＝常にこのグラフになるわけではない）ので注意してほしい。

　この結果から、x₀が4.0のときは、「猫」と分類されることになる。

　このようにソフトマックス関数は、主に分類問題におけるニューラルネットワークの出力層の活性化関数として用いられる。その場合、損失関数には（基本的に）交差エントロピー（Cross entropy、後日解説）が用いられる。

　主要ライブラリでは、次の関数／クラスで定義されている。

TensorFlow（2.x）／Keras： softmax()関数など
PyTorch： Softmaxクラスなど

定義と数式

　冒頭では文章により説明したが、厳密に数式で表現すると次のようになる。xやyはベクトル、nはクラスの数、iやkは特定のクラスを示すインデックスを意味する。

　e（オイラー数）や、それに対応するnp.exp(x)という後述のコードについては、「シグモイド関数」で説明しているので、詳しくはそちらを参照してほしい。オイラー数は、微分計算がしやすいというメリットがある。具体的に上記の数式の導関数（Derivative function：微分係数の関数）を求めると、次のように非常にシンプルな式になる。

Pythonコード

　上記のソフトマックス関数の数式をPythonコードの関数にするとリスト1のようになる。なお、テンソル（多次元配列）の計算を簡単にするため、ライブラリ「NumPy」をインポートして使った。

import numpy as np

def softmax(x):
if (x.ndim == 1):
x = x[None,:] # ベクトル形状なら行列形状に変換
# テンソル（x：行列）、軸（axis=1：列の横方向に計算）
return np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)

# 入力（x）と出力（y）の例
x = np.array([[1,0,0], [0,1,0], [0,0,1]])
y = softmax(x)
print(y) # 以下のように出力される
# [[0.57611688 0.21194156 0.21194156] # → 猫：全部足すと「1.0」になる
# [0.21194156 0.57611688 0.21194156] # → 虎： Σ＝1.0
# [0.21194156 0.21194156 0.57611688]] # → ライオン： Σ＝1.0

リスト1　ソフトマックス関数のPythonコード例

　ソフトマックス関数の導関数（derivative function）のPythonコードも示しておくと、リスト2のようになる。

# ※リスト1のコードを先に記述する必要がある

def der_softmax(x):
y = softmax(x)                        # ソフトマックス関数の出力
jcb = - y[:,:,None] * y[:,None,:]     # ヤコビ行列を計算（i≠jの場合）
iy, ix = np.diag_indices_from(jcb[0]) # 対角要素のインデックスを取得
jcb[:,iy,ix] = y * (1.0 - y)          # 対角要素値を修正（i＝jの場合）
return jcb                            # 微分係数の行列（ヤコビ行列）を出力

der_y = der_softmax(x)
print(der_y) # 以下のように出力される
# [[[ 0.24420622 -0.12210311 -0.12210311]
# [-0.12210311 0.16702233 -0.04491922]
# [-0.12210311 -0.04491922 0.16702233]]
#
# [[ 0.16702233 -0.12210311 -0.04491922]
# [-0.12210311 0.24420622 -0.12210311]
# [-0.04491922 -0.12210311 0.16702233]]
#
# [[ 0.16702233 -0.04491922 -0.12210311]
# [-0.04491922 0.16702233 -0.12210311]
# [-0.12210311 -0.12210311 0.24420622]]]

リスト2　ソフトマックス関数の「導関数」のPythonコード例

「AI・機械学習の用語辞典」

ここを更新しました（2023年10月2日）

冒頭の定義の説明を「ベクトル」の変換であることが分かるように修正し、図1内のグラフの作成方法についてより詳しく追記、数式の注釈も追記しました。