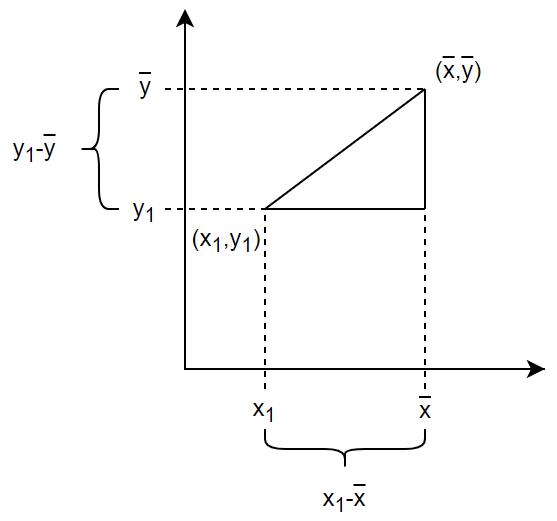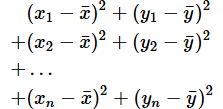［AI・機械学習の数学］総和を表すΣは機械学習に必須の記号：AI・機械学習の数学入門（5/5 ページ）

「Σ」を理解して総和をマスターしよう。応用で、Σの公式を使って平均を求めてみる（最小二乗法につながる基礎知識）。さらに、平均を使って重心を求める計算も行う（クラスタリング「k-means法」につながる基礎知識）。

[羽山博，著]

応用：重心を求める

　もう少し応用的なお話もしておきましょう。機械学習の一つにクラスタリングと呼ばれる方法があります。これは、データを幾つかのグループに分けるのに使われる手法です。そのときに、各グループのデータの「重心」を求める必要があり、そのためにも平均値が使われます。

　重心とは、各データからの距離の二乗和が最小になる点のことなので、やはり平均値に他なりません。小学校の頃から慣れ親しんできた平均値がここでも大活躍です。

　平面上の二点の距離を求める方法については、この連載の第1回で見ました。そのときには具体的な数値を使って計算しましたが、文字式を使って表してみましょう。

は、図4の斜辺の長さに当たります。

図4　2点の距離

　ピタゴラスの定理を使って計算すると、

は、

ですね。いちいち√を求めるのも面倒なので、2乗のままにしておきましょう。つまり、

は、

ということになります。

　次に、複数の点の重心を求めてみましょう。重心の座標を

とします。

が

を求めればいいですね。

図5　重心

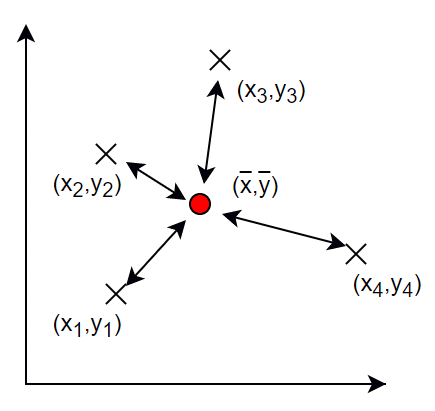
　上の図では、点は4つしか描かれていませんが、点が(x₁,y₁),(x₂,y₂)...(x_n,y_n)のようにたくさんあるなら、

は、

となりますね。これをΣを使って表せば、

となります。この式の値を最小にする

の値は、それぞれの平均値なので、

です。これが重心の座標です*2。

*2　

を求めるためには、微分法（偏微分）を使うのが便利です。いずれお話することになると思います。お楽しみに。

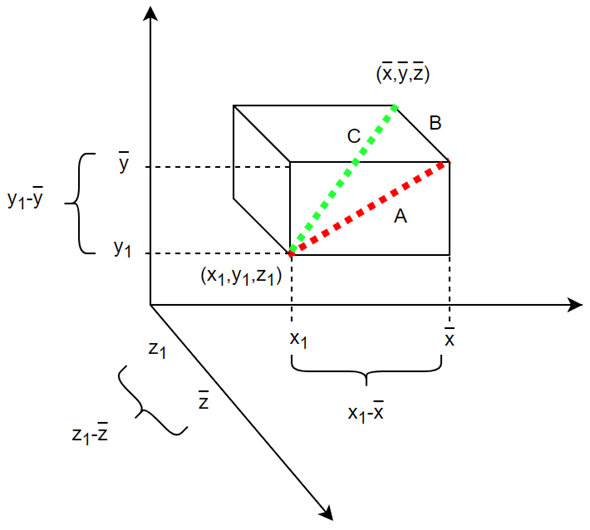
　軸（変数）がもう一つ増えて、三次元になっても同様に計算できます（図6）。考え方は同じですが、ちょっと複雑に見えるので、動画での解説も用意してあります（動画3）。

動画3　重心の座標を求める（三次元編）

図6　2点の距離（三次元）

　求めたい距離は、

で、図6のCの長さに当たります。ここでは、三角形ABCが直角三角形になっていることに注目してください。直角三角形ということは、やはりピタゴラスの定理が使えますね。つまり、

です。

　A²は上で求めた通り、

です。B²は

です。よって、C²は、

であることが分かります。

　重心も同様に求められます。点が(x₁,y₁,z₁),(x₂,y₂,z₂)...(x_n,y_n,z_n)のようにたくさんあるなら、

は、二次元の場合と同様、

となり、この式の値が最小になるときの

の値は、それぞれの平均値なので、重心の座標は、

となります。さらに変数が増えても考え方は同じです*3。

*3　軸の数が増えてくるとx,y,zでは変数を表しにくくなるので、x₁,x₂,x₃,...のように添字を使って変数を区別することがあります。この場合の添字は個々のデータを区別するものではなく、あくまで軸（変数）を区別するためのものです。従って、x₁とx₂は別の変数です（xという変数の1番目と2番目ではありません！）。x₁という変数の個々のデータを区別するためには、もう一つ添字を使って、

のように表します。これは、x₁という変数の1番目の値、x₁という変数の2番目の値、...、x₁という変数のn番目の値という意味になります。

　ちなみに、m次元のn個の点の重心の座標は、

と表されます。

　ここではクラスタリングなどの詳細については触れませんが、例えばk-means法では、以下のような手順でグループを分けます（これまでに学んだ知識だけでできます）。

1. 最初はランダムに幾つかのグループの重心の座標を決める
2. 各点を、重心との距離が一番近いグループに入れる
3. 各グループの重心の座標を計算し直す
4. 2に戻る（重心が動かなくなるまで繰り返す）

*余談　これまで、機械学習で使われる数学を理解するためにx,y,zといった変数を使って数式の意味や使い方を解説してきました。それでは実感が湧かない、現実の仕事にどう使われているのか分からないという人も多いでしょう。

　今回のお話とは異なる例ですが、重回帰分析では「面積」「駅歩」から「家賃」を予測するというようなことを行います。この場合は「面積」をx、「駅歩」をy、「家賃」をzで表す、と考えれば実感が湧くのではないかと思います。さらに「築年数」も考慮すると、変数が多くなって、文字が足りなくなるので、「面積」をx₁、「駅歩」をx₂、「築年数」をx₃という変数で表し、「家賃」をyという変数で表すといった方法を使います。

　念のために繰り返しておきますが、この場合の添字は各データを区別するためのものではなく、変数を区別するためのものです。

次回は……

　これまでのお話では二次式までしか扱ってきませんでした。機械学習では、三次、四次といった高次の関数や指数関数、対数関数などを扱うことも考えられます。また変数をたくさん使い、それらの連立方程式を解く、といったことも必要になってきます。さらに、値の変化を見て最適な解を求めることもあります。そういった問題を解決するための強力な助っ人が「微分」です。

　次回は、微分法を取り上げ、さまざまな関数の解析ができるようにするための基礎を学びます。計算方法は平方完成よりもはるかに簡単なので、ご心配なく。

「AI・機械学習の数学入門」