第8回 分類問題をディープラーニング(基本のDNN)で解こう:TensorFlow 2+Keras(tf.keras)入門(2/3 ページ)
回帰問題の次は、分類問題の基礎をマスターしよう。二値分類/多クラス分類の場合で一般的に使われる活性化関数や損失関数をしっかりと押さえる。また過学習問題の対処方法について言及する。
―――【多クラス分類編】―――
それでは準備が整ったとして、(1)から順に話を進めていこう。
(1)データの準備
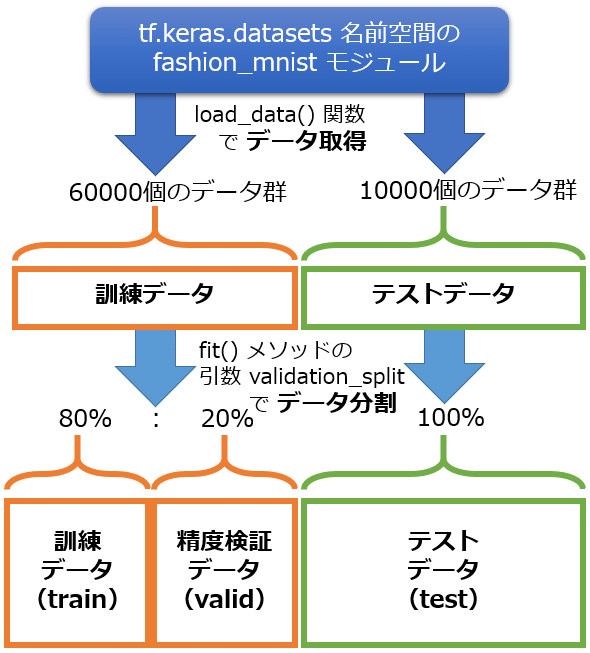
前述の通り、多クラス分類問題では「Fashion-MNIST」データセットを用いる。このデータセットは、TensorFlowやtf.kerasで簡単に導入できるので、特別な準備は必要ない。Fashion-MNISTデータセットの内容は、図5に示すようなファッション商品の小さな写真であり、教師データとなるラベルには、分類カテゴリーごとに(商品カテゴリー名ではなく)0〜9のクラスインデックスが指定されているので、カテゴリー変数エンコーディングの作業も不要である。
実際にtf.kerasを使ってtf.keras.datasets.fashion_mnist.load_data()というコードで、Fashion-MNISTデータセットを取得しているのがリスト1-1である(※重要箇所は太字にした)。
# TensorFlowライブラリのtensorflowパッケージを「tf」という別名でインポート
import tensorflow as tf
import matplotlib.pyplot as plt # グラフ描画ライブラリ(データ画像の表示に使用)
import numpy as np # 数値計算ライブラリ(データのシャッフルに使用)
# Fashion-MNISTデータ(※NumPyの多次元配列型)を取得する
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# データ分割は自動で、訓練用が6万枚、テスト用が1万枚(ホールドアウト法)。
# さらにそれぞれを「入力データ(X:行列)」と「ラベル(y:ベクトル)」に分ける
# ※訓練データは、学習時のfit関数で訓練用と精度検証用に分割する。
# そのため、あらかじめ訓練データをシャッフルしておく
p = np.random.permutation(len(X_train)) # ランダムなインデックス順の取得
X_train, y_train = X_train[p], y_train[p] # その順で全行を抽出する(=シャッフル)
# [内容確認]データのうち、最初の10枚だけを表示
classes_name = ['T-shirt/top [0]', 'Trouser [1]', 'Pullover [2]',
'Dress [3]', 'Coat [4]', 'Sandal [5]', 'Shirt [6]',
'Sneaker [7]', 'Bag [8]', 'Ankle boot [9]']
plt.figure(figsize=(10,4)) # 横:10インチ、縦:4インチの図
for i in range(10):
plt.subplot(2,5,i+1) # 図内にある(sub)2行5列の描画領域(plot)の何番目かを指定
plt.xticks([]) # X軸の目盛りを表示しない
plt.yticks([]) # y軸の目盛りを表示しない
plt.grid(False) # グリッド線を表示しない
plt.imshow( # 画像を表示する
X_train[i], # 1つの訓練用入力データ(28行×28列)
cmap=plt.cm.binary) # 白黒(2値:バイナリ)の配色
plt.xlabel(classes_name[y_train[i]]) # X軸のラベルに分類名を表示
plt.show()
このコードを実行すると、データセットの最初の10枚の画像を2行5列で表示する(※写真自体は図5で示したので、実行結果の掲載は省略した)。
リスト1-1を見ると、今回は、データセットとして、
- 訓練データ: 入力データとなる特徴量X_trainと、正解となるラベルy_train
- テストデータ: 特徴量X_testと、ラベルy_test
の2種類を用意しているのが分かる。ちなみにこのような分け方をホールドアウト法(Hold-out method)と呼ぶ。連載中に何度も言及しているが、テストデータ(ホールドアウトデータ、Hold-out setsとも呼ぶ)は最終的な性能テストに使うので、訓練時の精度検証には使わないように別枠で取っておかなければならい。
「あれ? 精度検証データは?」と思った人は鋭い。ホールドアウト法は、統計学/データサイエンスの重回帰分析をする場合などでは有効である。しかし、ニューラルネットワーク(ディープラーニング)では、過学習などが起こりやすいのでハイパーパラメーターのチューニングを行う必要があり、そのため、精度を検証(validation)するためのデータも必要となるのだ。
繰り返しになるが、この検証作業にテストデータを使ってはいけない。機械が何度もトレーニングすることによって訓練データへの過学習が生まれるように、人間が何度もチューニングすることによって精度検証データへの偏向が生まれている可能性がある。そのため、「そういった過学習や偏向が確実にない」と言える未知のテストデータに対しても(つまり汎用的に)、学習済みモデルが本当に使える性能を発揮するか(=汎化性能)を最終テストした方がよいからだ。
そういった理由で、訓練データの中から精度検証データを分離する必要があるのだ(※本連載では「精度検証」と呼んでいるが、正式には単に「検証」が正しい。ただし、「検証」と「テスト(検定)」の違いが「特に初学者には分かりづらい」と想定して、あえて「精度検証」と呼んでいる)。チュートリアルや書籍によっては、テストデータで検証しているが、これは「テストデータ」という名前の「精度検証データ」なのだ、と捉えてほしい。
で、なぜここで、前回までのように、
- 精度検証データ: 特徴量X_validと、ラベルy_valid
を作成しないかというと、tf.kerasのfit()メソッドにvalidation_split引数が用意されており、そこに任意の精度検証データの割合を指定できるからだ。割合として、例えば20%(=0.2)を指定すると、訓練データが「訓練データ80%」と「精度検証データ20%(=0.2)」に分割される(本当に便利な機能である)。
ちなみに、validation_split引数の指定は「訓練データの後ろから何%」という固定的な分割方法になる。そのため、リスト1-1で事前に訓練データをシャッフルして、データが固定的にならないようにしておいたのだ。このように検証を固定的にしない別のアプローチに、交差検証(Cross validation)というテクニックがある。交差検証の中でも特に有名なのがk分割交差検証(k-fold cross validation)で、具体的にはデータをK個(例えば5個)に分割して、その1つを検証データとして、訓練のたびに検証データの位置を(例えば、1個目、2個目、3個目、4個目、5個目、……と)ずらしながら繰り返し学習していく。特に訓練データ数が少ない場合には、k分割交差検証が効果的である。……と、このような説明だけでは伝わらないと思うが、交差検証だけで記事が1本書けるので、より詳しくは今後の連載に委ねることにする。
まとめると、最終的なデータ分割は図6のようになる。
また前回同様、ミニバッチ学習用のデータ分割は、fit()メソッドが自動的に行ってくれるため、今回もバッチデータ化は行わない。
MNIST系の画像データセットのフォーマットについて
これまでの連載では、座標点という非常にシンプルなデータを扱ってきたので、「画像データ」というのがどういうデータで、それがどのように入力されるのか、想像が付かないという人もいるだろう。そこで画像データセットのフォーマットについて簡単に説明しておく。
取りあえず、訓練データの1つ目の入力データとラベルを、出力して確かめてみよう(リスト1-2)。
import pandas as pd # データ解析支援「pandas」
# 1件の訓練データの、ラベルと入力データを表示する
print('y_train(正解ラベル): 「',y_train[0],'」');
print('X_train:');
display(pd.DataFrame(X_train[0])) # NumPy多次元配列をpandasデータフレームに変換して表示
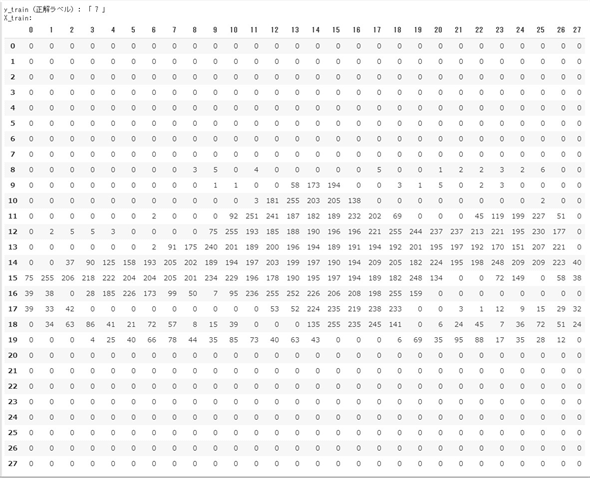
このコードを実行した結果、筆者の場合は図7のように表示された(※訓練データはシャッフルしたので、結果が人によって異なる)。
1つ目のデータの正解ラベルは「7」(=Sneaker)となっている。なお、前掲のリスト1-1のコードからも分かったと思うが、Fashion-MNISTデータセットは10個の分類カテゴリーのデータとなっており、0スタートで次のようにクラスインデックスが定義されている。
- ラベル「0」: T-shirt/top(Tシャツ/トップス)
- ラベル「1」: Trouser(ズボン)
- ラベル「2」: Pullover(プルオーバー、頭から被って着る服)
- ラベル「3」: Dress(ドレス)
- ラベル「4」: Coat(コート)
- ラベル「5」: Sandal(サンダル)
- ラベル「6」: Shirt(シャツ)
- ラベル「7」: Sneaker(スニーカー)
- ラベル「8」: Bag(バッグ)
- ラベル「9」: Ankle boot(アンクルブーツ、かかとが隠れる丈のブーツ)
入力データの方は、28行×28列の表形式で出力されている。各セル内には0〜255(256段階)の数値が入っており、それぞれが画像内の1つの画素(ピクセル)に相当する。数値は0が「白色」を意味し、255が「黒色」を意味する。Web開発をしている人は「光の三原色」であるRGB(赤色/緑色/青色)形式に詳しいと思うが、RGBでは色が重なるほど白くなるので、
- (R=0、G=0、B=0)が黒色で、(R=255、G=255、B=255)が白色
になる仕様である。よってRGBとは、正反対の数値範囲の仕様
- 0=白色、255=黒色
になっていることに注意してほしい。
ちなみに「28行×28列」「0〜255」「0=白色、255=黒色」といった仕様は、後述の二値分類編で使うMNISTデータセットの制作者(Yann LeCun氏ら)のサイトに載っている(※Fashion-MNISTデータセットは、より手応えのある代わりのMNISTデータセットとして使えるように、MNISTデータセットの仕様に合わせて作られている)。具体的には、「FILE FORMATS FOR THE MNIST DATABASE(MNISTデータベースのファイルフォーマット)」欄に、
- 「28(number of rows:行数)×28(number of columns:列数)」
- 「Pixels are organized row-wise. Pixel values are 0 to 255. 0 means background (white), 255 means foreground (black).
(画像のピクセルデータは行ごとに並んでいる。ピクセルの値は0〜255。0は背景/白色、255は前景/黒色を意味する。)」
のように記載されている(※チュートリアルやサンプルによっては、RGBに合わせて「255=白色、0=黒色」と定義している場合もある。本稿では上記の定義を採用した)。ちなみに前掲のリスト1-1で、白黒(2値:バイナリ)の配色(カラーマップ)として
- cmap=plt.cm.binary
を指定したが、これを
- cmap=plt.cm.gray
にすると黒白(RGBグレースケール)の配色で画像を表示できる。
入力データの正規化(Normalization)
今回の入力データは、28行×28列の画素データのみなので、
- 0〜255
という数値範囲のまま使うことも不可能ではないが、通常、機械学習(特に画像の画素データ)では、データの数値範囲を、
- 0.0〜1.0
にスケーリングして、他の入力データ(特徴量)との数値範囲の違いが無くなるように加工する。この加工テクニックを正規化(Normalization、厳密にはMin-Max normalization:最小値・最大値の正規化)と呼ぶ。
今回のような「画素データの正規化」によって、トレーニングでの収束が速くなる(=学習時間がより短くて済む)などの効果がある。よって今回も正規化を実施しておこう。
X_train = (X_train / 255.0).astype(np.float32)
X_test = (X_test / 255.0).astype(np.float32)
といっても難しくはない。リスト1-3のように「0〜255」の範囲数値を255.0で割ることで、0.0〜1.0にスケーリングされる。
ちなみに数値計算ライブラリ「NumPy」は、デフォルトでfloat64型(64ビットの浮動小数点数型)の値となるが、TensorFlowの基本はfloat32型(32ビットの浮動小数点数型)なので数値のデータ型を変換しておく。
(2)モデルの定義
ニューラルネットワークのモデルの書き方について再確認しておこう。今回も以下の書き方を採用する。
- tf.keras.Modelクラスをサブクラス化してモデルを定義する(初中級者以上にお勧め)
- tf.kerasの基本であるcompile()&fit()メソッドを使用する(今回はカスタムループの実装は不要なため)
ディープニューラルネットワークのモデル設計
ニューラルネットワークのモデル設計は、以下の仕様とする(※本稿の場合。もちろん、これ以外の仕様を定義してもよい。これは筆者が試行錯誤した後、より説明しやすいネットワーク構造を選択した結果である)。
- 入力の数(INPUT_FEATURES)は、28行×28列(=784)になっているので、フラット化(Flatten)して784個
- 隠れ層のレイヤー数は、2つ
- 隠れ層にある1つ目のニューロンの数(LAYER1_NEURONS)は、128個
- 隠れ層にある2つ目のニューロンの数(LAYER2_NEURONS)は、32個
- 出力層にあるニューロンの数(OUTPUT_RESULTS)は、10個
今回の入力データは、前述の通り28行×28列(=784個)となっており、それをフラットな1行に変換することで、入力層の特徴量(features: 特徴を表現する数値)は784個になる。784個の特徴量が、128個の特徴量、32個の特徴量、10個の特徴量と次第に絞られることで、全画素という生画像データそのものに近い低次の特徴から、徐々に高次の特徴を発見していき(=一般的には「自動的に特徴を獲得する」と表現される)、最終的にクラス分類を行うという流れを意識して、各層におけるニューロンの数を決定した。
今回の隠れ層の活性化関数は、最も一般的なReLU関数を使用する(前回までは基礎的なTanh関数を使っていた)。現在のディープラーニングでは、まずはReLU関数を使うことが基本であるので覚えておいてほしい。
また、出力層の活性化関数は、前述した通り、多クラス分類時に一般的に利用されるソフトマックス関数を指定する。
以上の仕様に基づくニューラルネットワークのモデル設計コードは次のようになる。コード全体の説明はもう不要だろう(※重要箇所は太字にした)。
import tensorflow as tf # ライブラリ「TensorFlow」のtensorflowパッケージをインポート
from tensorflow.keras import layers # レイヤー関連モジュールのインポート
# 定数(モデル定義時に必要となるもの)
INPUT_ROWS = 28 # 入力行の数: 28行
INPUT_COLS = 28 # 入力列の数: 28列
# 入力(特徴)の数: 784(=28行×28列)
LAYER1_NEURONS = 128 # ニューロンの数: 128
LAYER2_NEURONS = 32 # ニューロンの数: 32
OUTPUT_RESULTS = 10 # 出力結果の数: 10(=「0」〜「9」の10クラスに分類)
#OUTPUT_RESULTS = 1 # 後述する二値分類の場合: 1(=「0.0」〜「1.0」の2値に分類)
# 過学習対策でドロップアウトを使う場合はコメントオフ:
#DROPOUT1_RATE = 0.2 # 第1隠れ層から第2隠れ層へのドロップ率: 0.2(20%)
# 変数(モデル定義時に必要となるもの)
activation1 = layers.ReLU(name='activation1') # 活性化関数(隠れ層用): ReLU関数(変更可能)
activation2 = layers.ReLU(name='activation2') # 活性化関数(隠れ層用): ReLU関数(変更可能)
act_output = layers.Softmax(name='act_output') # 活性化関数(出力層用): Softmax関数(固定)
# tf.keras.Modelによるモデルの定義
class NeuralNetwork(tf.keras.Model):
# レイヤー(層)を定義
def __init__(self):
super().__init__()
# 入力層:入力データのフラット化(Flatten)
self.flatten_input = layers.Flatten( # 行列データのフラット化
input_shape=(INPUT_ROWS, INPUT_COLS), # 入力の形状(=入力層)※タプル形式
name='flatten_input')
# 隠れ層:1つ目のレイヤー(layer)
self.layer1 = layers.Dense( # 全結合層(線形変換)
# 入力ユニット数は、前の出力ユニット数が使われるので、指定不要
LAYER1_NEURONS, # 次のレイヤーへの出力ユニット数
name='layer1')
# 第1レイヤーの後でドロップアウトを使う場合はコメントオフ:
#self.dropput1 = layers.Dropout( # ドロップアウト
# DROPOUT1_RATE, # 何%ドロップするか
# name='dropput1')
# 隠れ層:2つ目のレイヤー(layer)
self.layer2 = layers.Dense( # 全結合層
LAYER2_NEURONS, # 次のレイヤーへの出力ユニット数
name='layer2')
# 出力層
self.layer_out = layers.Dense( # 全結合層
OUTPUT_RESULTS, # 出力結果への出力ユニット数
name='layer_out')
# フォワードパスを定義
def call(self, x, train_mode=True):
x = self.flatten_input(x) # 入力データのフラット化
# 「出力=活性化関数(第n層(入力))」の形式で記述
x = activation1(self.layer1(x)) # 活性化関数は変数として定義
#ドロップアウトを使う場合はコメントオフ:
#if train_mode: # 訓練時のみ……
# x = self.dropput2(x) # ……ドロップアウト(不活性化)
x = activation2(self.layer2(x)) # 活性化関数は変数として定義
x = act_output(self.layer_out(x)) # ※活性化関数は「softmax」固定
return x
# モデル内容の出力を行う独自メソッド
def get_static_model(self):
x = layers.Input(shape=(28,28), name='input_features')
static_model = tf.keras.Model(inputs=[x], outputs=self.call(x))
return static_model
見知らぬ部分は、入力層にFlattenクラスが使われている点だろう。これにより、前述のフラット化を実現している。
他には、ニューロンの数や活性化関数が変わっている。それ以外は、前回とほとんど変わらないコードである。前回と同様に、実装しているget_functional_modelメソッドは、次のリスト2-2でモデル内容を描画するために用意した独自の関数である(本来の処理には不要。第5回で説明済み)。
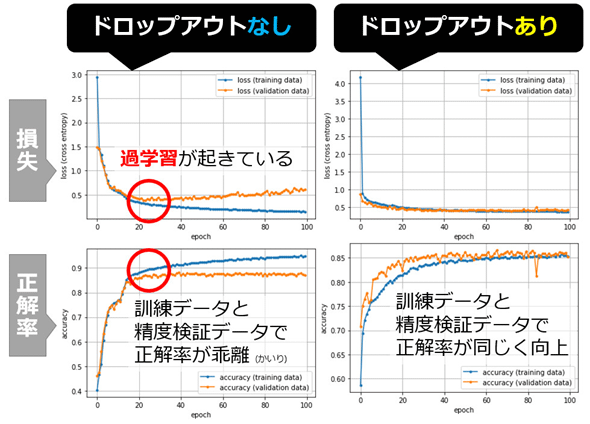
「ドロップアウト」と書かれてコメントアウトされている箇所があるが、ドロップアウト(Dropout)とは主に過学習を防ぐためのテクニックである。特に特徴量/ニューロンの数が多い複雑なネットワークの場合は、本来は不要なニューロン(いわばノイズ)も数多く含まれていると考えられるので、そのノイズを学習してしまうことで学習が安定しなかったり過学習(Over-fitting:過剰適合)が起きたりしやすい。これを回避するために、一定割合のニューロンをランダムにドロップして(=落として)不活性化させながら学習するテクニックである。
例えばリスト2-1で「ドロップアウトしない」のまま訓練したのが図8の左で、「ドロップアウトした」状態で訓練したのが図8の右である。ドロップアウト「なし」では、途中から訓練データだけ損失が下がり、また正解率は上がり始め、精度検証データとの乖離(かいり)が大きくなっていっている。これは、訓練データに過剰に適合し過ぎた結果、つまり過学習なのである。このような過学習が、ドロップアウト「あり」では起きていないのが分かるだろう。
ドロップアウトについてもより丁寧に詳しく解説した方がよいと思うが、長くなるので本稿では雑感をつかんでいただくだけにとどめる。ちなみに過学習を防ぐ方法は他にもある。例えば、精度検証データの正解率が途中から改善しなくなった地点から過学習が発生していると考えられるが、改善しなくなった段階ですぐに学習をやめてしまえば、過学習は起きない。これが早期終了(Early Stopping:早期停止)である。tf.kerasでは早期終了は簡単に実装できるので、後述のリスト3-2ではコメントアウトした状態で含めている。他には、第2回で解説した正則化(Regularization)を用いる方法や、ニューロン数(ユニット数)を減らしたり、訓練データ数を増やしたりする方法などがある。
さて、少し脱線したが、モデル定義に話を戻す。定義したモデルを生成して内容を図で確認してみよう(リスト2-2)。
# モデル(NeuralNetworkクラス)のインスタンス化
model = NeuralNetwork()
# モデル概要の図を描画する
f_model = model.get_static_model()
filename = 'model.png';
tf.keras.utils.plot_model(f_model, show_shapes=True, show_layer_names=True, to_file=filename)
from IPython.display import Image
Image(retina=False, filename=filename) # 図で描画
#f_model.summary() # テキストで出力
Image(retina=False, filename=filename)
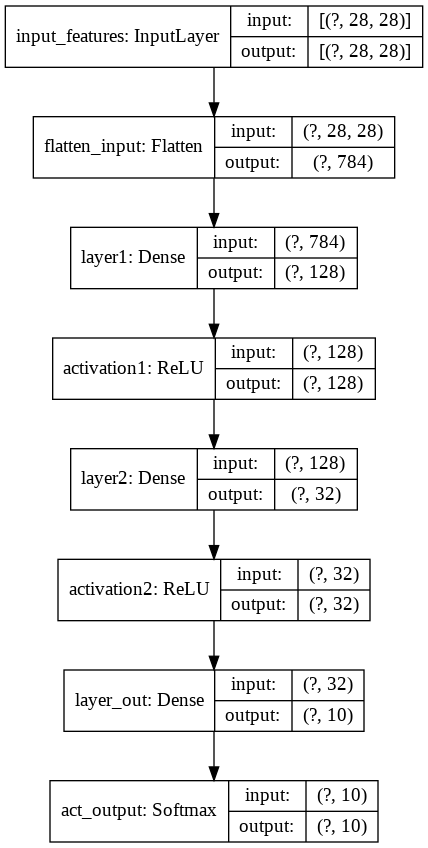
これを実行すると、図9のように描画される。
特に難しいところはないだろう。
(3)学習/最適化(オプティマイザ)
学習に関するコードも、使うものを細かく変えたが、設定項目自体はこれまでと変わらない。
# 定数(学習方法設計時に必要となる数値)
LOSS = 'sparse_categorical_crossentropy' # 損失関数:多クラス分類用の交差エントロピー
METRICS = ['accuracy'] # 評価関数:正解率
OPTIMIZER = tf.keras.optimizers.Adam # 最適化:Adam
LEARNING_RATE = 0.001 # 学習率: 0.001(学習率の調整)
# 学習方法を定義する
model.compile(optimizer=OPTIMIZER(learning_rate=LEARNING_RATE),
loss=LOSS,
metrics=METRICS) # 精度(分類では正解率。回帰では損失)
多クラス分類の問題で使うソフトマックス活性化関数とセットで、学習方法における損失関数には「多クラス分類用の交差エントロピー」を使うと既に説明した。'sparse_categorical_crossentropy'(スパースラベル対応の多クラス分類用の交差エントロピー)がそれである。ちなみに、スパースラベル(=クラスインデックス)ではなく、正解ラベルをone-hotエンコーディングした場合は、'categorical_crossentropy'(one-hot表現対応の多クラス分類用の交差エントロピー)を使えばよい。
精度指標となる評価関数は、分類問題なので「正解率(Accuracy)」を採用した。['accuracy']がその箇所だ。
また最適化アルゴリズム(オプティマイザ)には、最も一般的でよく使われているAdamを指定している(前回までは基礎的な「SGD:確率的勾配降下法」を使っていた)。現在のディープラーニングでは、まずはAdamを使うことが基本であるので覚えておいてほしい。なお、Adamの中身の計算式を知っておくに越したことはないが、知らなくても実用上の問題は基本的にないので、本稿では説明を割愛する。
最適化アルゴリズムに指定する学習率は、試行錯誤した結果、今回は0.001を指定している。
続いて、fit()メソッドを呼び出して、トレーニングを実施しよう(リスト3-2)。
# 定数(ミニバッチ学習時に必要となるもの)
BATCH_SIZE = 96 # バッチサイズ: 96
EPOCHS = 100 # エポック数: 100
# 早期終了
#es = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=3)
# 学習する
hist = model.fit(x=X_train, # 訓練用データ
y=y_train, # 訓練用ラベル
validation_split=0.2, # 精度検証用の割合:20%
batch_size=BATCH_SIZE, # バッチサイズ
epochs=EPOCHS, # エポック数
verbose=1, # 実行状況表示
callbacks=[ # コールバック
#es # 早期終了(する場合はコメントアウトを解除)
])
ミニバッチ学習のバッチサイズを96、トレーニング単位であるエポック数は100とした。なお、今回は入力データの数などが多いので、学習にしばらく(状況によるが3分近く)かかるので注意してほしい。
前述した通り、fit()メソッドにvalidation_split引数を指定して、訓練データが80%、精度検証データが20%(0.2)になるように、訓練データを分割している。
過学習を回避するためのテクニックの一つである早期終了(Early Stopping)のサンプルコードも、前述した通り、コメントアウトした状態で含めている。
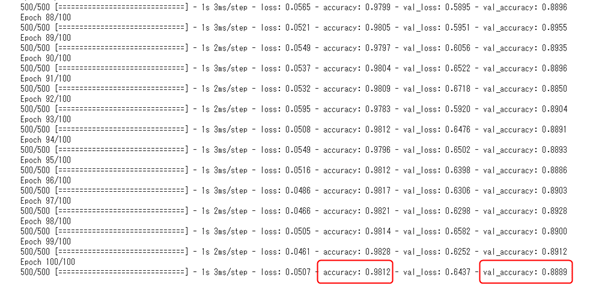
以上のリスト3-2までのコードを実行すると、モデルのトレーニングが実施される(図10)。
(4)評価/精度検証
あとは、出来上がった学習済みモデルの精度検証(validation)を行い、「このまま学習を完了とするか」「ハイパーパラメーター(=リスト2-1のモデル定義やリスト3-1の学習方法の定義、リスト3-2のトレーニングの各コード内に記載した各定数の値)を変えて試行錯誤するか」を決める。
今回は、学習結果として「損失」と「正解率」の履歴をグラフに描画してみよう(リスト4-1)。
import matplotlib.pyplot as plt
# 学習結果(損失=交差エントロピー)のグラフを描画
plt.figure()
train_loss = hist.history['loss']
valid_loss = hist.history['val_loss']
epochs = len(train_loss)
plt.plot(range(epochs), train_loss, marker='.', label='loss (training data)')
plt.plot(range(epochs), valid_loss, marker='.', label='loss (validation data)')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss (cross entropy)')
# 評価関数(正解率)のグラフを描画
plt.figure()
train_mae = hist.history['accuracy']
valid_mae = hist.history['val_accuracy']
epochs = len(train_mae)
plt.plot(range(epochs), train_mae, marker='.', label='accuracy (training data)')
plt.plot(range(epochs), valid_mae, marker='.', label='accuracy (validation data)')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
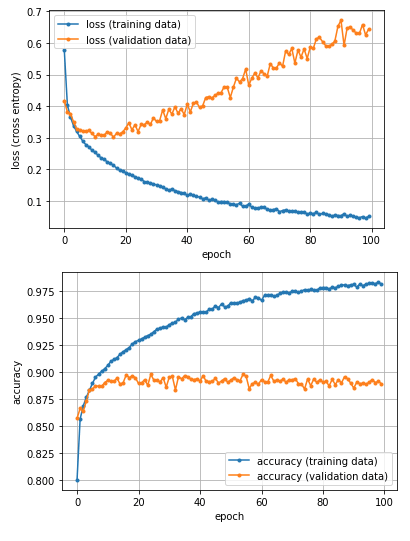
このコードを実行すると、筆者の場合は図11のようなグラフが描画された。
筆者の実行例では、途中から訓練データのみ損失が下がり、正解率が上がっており、精度検証データとの乖離(かいり)が大きくなっていっている。これは先ほども見たように過学習である。前回の図11と「損失のグラフ」を見比べると、その違いがよく分かるはずだ。
この状態では「完成」とはできずに、ハイパーパラメーターをチューニングして学習し直す必要があるだろう。今回は便宜上、この状態で次に進め、最後の汎化性能の評価を行うことにする。
(5)テスト/未知データによる評価
実際にテスト(=未知のテストデータを使って評価)を行うコードがリスト5-1だ。
#BATCH_SIZE = 96 # バッチサイズ(リスト3-2で定義済み)
# 未知のテストデータで学習済みモデルの汎化性能を評価
score = model.evaluate(X_test, y_test, batch_size=BATCH_SIZE)
print('test socre([loss, accuracy]):', score)
# 出力例:
# 105/105 [==============================] - 0s 1ms/step - loss: 0.7703 - accuracy: 0.8766
# test socre([loss, accuracy]): [0.7702566981315613, 0.8766000270843506]
このコードを実行した結果、評価関数('accuracy':正解率)の結果値として0.8766が出力された。この数値は、前述の訓練データに対する最終的な正解率(0.9812)とは大きく違う(=10.4%以上の差がある)ので、汎化性能として問題がある。つまり過学習などの問題がある、と分かる。
実運用のイメージ
多次元クラス編の最後に、独自のデータを仮作成して、それを使って推論する過程を体験してみよう。
まずはリスト5-2のコードにより、1つのデータを手動で作成してみよう。
import matplotlib.pyplot as plt # グラフ描画ライブラリ(データ画像の表示に使用)
#import pandas as pd # データ解析支援「pandas」
temp_data = np.array([[ # 9番:アンクルブーツ
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 31,178,162,153,151,142,138, 65, 0, 0, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 78,232,209,202,198,194,203,179, 97, 89, 73, 59, 47, 28, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,121,228,202,196,189,185,175,198,244,245,232,223,218,160, 4, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,157,223,203,199,192,176,186,215,235,228,220,216,214,164, 8, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 12,192,216,204,198,185,179,211,228,232,225,220,216,213,159, 6, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 40,214,210,201,195,182,191,223,232,233,227,224,219,216,150, 2, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 75,224,203,197,193,182,202,229,231,233,230,228,220,217,140, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,113,228,198,188,188,187,208,229,230,234,232,230,220,215,164, 4, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,154,226,197,182,184,189,210,228,231,234,233,231,221,213,196, 35, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10,190,219,193,183,184,190,210,228,232,234,233,232,223,212,211, 96, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 39,214,212,186,181,183,189,207,225,230,232,233,232,223,212,208,151, 2],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 80,227,208,185,179,183,192,205,210,222,229,229,231,225,214,204,177, 21],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,122,229,206,185,180,184,192,196,192,215,226,232,234,226,215,205,177, 24],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 3,169,225,208,188,180,189,187,180,170,218,235,234,224,217,212,210,160, 10],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 38,212,220,206,179,179,190,186,173,182,229,229,220,213,211,210,207, 84, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0,101,229,216,197,177,188,191,180,187,219,222,214,218,216,211,212,177, 19, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 5,174,226,211,190,179,189,191,189,215,217,213,216,167,174,211,210,131, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 62,221,218,203,183,179,185,198,214,214,214,214, 96, 2, 25,198,214, 79, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 11,166,225,211,192,177,184,203,216,216,212,212, 69, 0, 0, 14,190,204, 34, 0, 0],
[ 0, 0, 0, 0, 0, 0, 22,127,219,219,206,187,178,198,223,221,212,219, 86, 0, 0, 0, 11,190,181, 9, 0, 0],
[ 0, 0, 0, 2, 33, 92,165,204,211,208,191,185,201,220,228,220,224,134, 0, 0, 0, 0, 14,198,157, 0, 0, 0],
[ 0, 21,102,160,192,212,214,199,193,193,182,199,220,226,224,219,202, 26, 0, 0, 0, 0, 16,205,137, 0, 0, 0],
[ 44,193,227,222,217,212,205,190,183,186,198,225,230,228,218,224,111, 0, 0, 0, 0, 0, 17,209,122, 0, 0, 0],
[109,230,213,208,205,205,204,198,196,205,215,227,229,225,221,205, 24, 0, 0, 0, 0, 0, 15,208,113, 0, 0, 0],
[ 25,103,159,193,213,218,215,215,213,213,215,217,220,225,229, 97, 0, 3, 3, 3, 2, 0, 25,225,114, 0, 1, 0],
[ 0, 0, 7, 44,100,150,177,192,203,209,212,215,216,198,110, 17, 15, 12, 10, 9, 8, 4, 30,153, 77, 1, 1, 1],
[ 0, 0, 0, 0, 0, 0, 5, 15, 23, 31, 35, 37, 34, 17, 2, 4, 2, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0]
]], dtype=float)
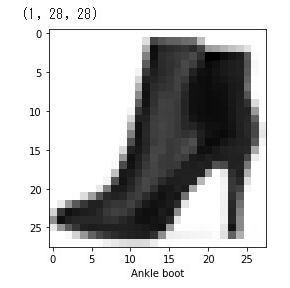
print(temp_data.shape) # 多次元配列の形状: (1, 28, 28)
# 図を描画
plt.imshow( # 画像を表示する
temp_data[0], # 1つの訓練用入力データ(28行×28列)
cmap=plt.cm.binary) # 白黒(2値:バイナリ)の配色
plt.xlabel('Ankle boot') # X軸のラベルに分類名を表示
plt.show()
#display(pd.DataFrame(temp_data[0])) # 表形式で表示する場合
ちなみにこのデータは、Fashion-MNISTデータセットのものではなく、筆者が手動で作成したものである。今後のディープラーニングの実践のためにも、自分でMNIST系画像データを作れるようになりたいという人もいるかもしれない。その方法についての説明は割愛するが、後述の「リスト10-2 推論: 手書き文字データを自作」が参考になるだろう。
リスト5-2を実行すると、図12のようなAnkle boot(対応するクラスインデックス:9)の画像が表示される。
次に、いつも通りにpredict()メソッドで推論すればよい(リスト5-3)。
import matplotlib.pyplot as plt # グラフ描画ライブラリ(データ画像の表示に使用)
# 推論(予測)する
predictions = model.predict(temp_data)
print(predictions)
# 以下のように出力される(インデックス番号「9」が99.88%)
# array([[1.50212283e-20, 1.48110773e-15, 1.04932664e-13, 2.96827862e-12,
# 6.80513210e-08, 5.95744408e-04, 1.75191891e-18, 6.33274554e-04,
# 6.95163068e-12, 9.98770893e-01]], dtype=float32)
# 数値が最大のインデックス番号を取得(=分類を決定する)
pred_class = np.argmax(predictions, axis=-1)
print(pred_class) # 9 (=Ankle boot)……などと表示される
推論された予測値は、ソフトマックス関数により10クラスの合計の数値が100%(=1.0)になる。出力された10個の数値から一番大きな数値を探せばよいが、数値の桁数が多く、読み取りづらい。そこで、NumPyのargmax()関数を使って各行の中で最大の数値を持つ要素の配列インデックスを取得すればよい。この配列インデックスは、クラスインデックスと一致する。ちなみに引数のaxisについては、「Lesson 3 NumPyによる数学計算と、数学用語の「テンソル」:機械学習&ディープラーニング入門(データ構造編) - @IT」でも説明しているが、ここでの予測値は行列データなので軸(axis)は行方向(0)と列方向(1)があり、-1は最後の軸、つまり列方向(1)を意味する。列方向に配列の要素が10個並んでおり、その中から最大値を見つけるということである。
以上で分類結果は十分に分かると思うが、より視覚的に見たい場合は、リスト5-4のようなコードを書けばよい。
x = range(10) # 0, 1, 2, ……, 9
thisplot = plt.barh(x, predictions[0])
plt.xlim([0.0, 1.0])
classes_name = ['T-shirt/top [0]', 'Trouser [1]', 'Pullover [2]',
'Dress [3]', 'Coat [4]', 'Sandal [5]', 'Shirt [6]',
'Sneaker [7]', 'Bag [8]', 'Ankle boot [9]']
plt.yticks(x, classes_name) # X軸のラベル
plt.gca().invert_yaxis()
plt.show()
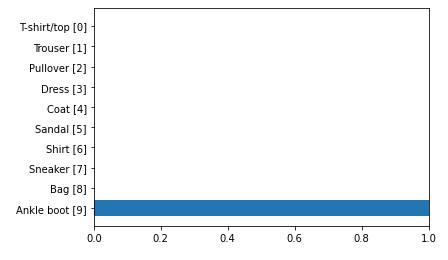
このコードを実行すると、図13のように横棒グラフで表示され、「どのカテゴリーが何%か」という比較がしやすい。といってもこの例では、リスト5-3から分かるように99.9%「Ankle boot」(クラスインデックス:9)と判定されているので、他のクラスインデックスと比較することはできないが。
次のページは……
以上で多クラス分類の習得は完了だ。説明不要な箇所は省略して進めてきたが、それでもかなり疲れてきていることだろう。しかしもう少しだけ話を進めさせてほしい。というのも、多クラス分類と二値分類はセットで理解した方が効率がよいからである。ただし、多くのコードは重複するので、説明は極力なしで、書き換えたコードのみを太字で示していく。コード自体は全体を掲載するので長いが、太字以外は読み飛ばしていただいて構わない。
二値分類編の説明は、次のページで行う。
Copyright© Digital Advantage Corp. All Rights Reserved.