RNNに触れてみよう:サイン波の推測:作って試そう! ディープラーニング工作室(1/2 ページ)
RNNを見ていくその手始めとして、サイン波のグラフを構成する値から、連続するデータの次の値が何かを推測したり、その推測値を基にグラフをプロットしたりしてみます。
前回までは、CNNの基本的な動作について説明をして、MNISTの手書き数字を関数にまとめて、その結果をグラフに描画するといった話をしてきました。今回からは数回に分けて、RNN(Recurrent Neural Network)がどんなものかを見ていきましょう。
RNNとは
RNN(Recurrent Neural Network)とは、「時系列データをうまく扱う」のに適したニューラルネットワークです。ここでいう「時系列データ」とは、連続する複数のデータが時間軸に沿ったものであったり、何らかの順序で並んでいたりするもののことです。数年間にわたる降水量のデータを日ごとにまとめたデータは想像しやすい時系列データの一つでしょう。あるいは「Python is great !」(Pythonはスゴイ!)という英単語の綴りもまた時系列データの一つといえます。この文は「主語 述語 形容詞 感嘆符」という4つの語が一定の規則に従って並べられたもので、こうしたものもRNNでは時系列データとして扱えます。
時系列データを扱う際に重要になるのは、ある時点のデータが、それ以降のデータに影響を与えている(と見なせる)という点です。例えば、サイン波について考えてみましょう。
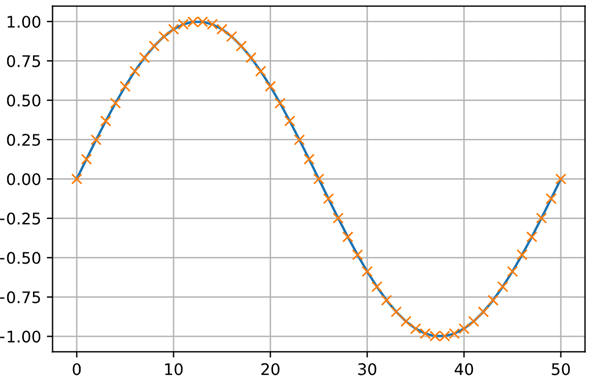
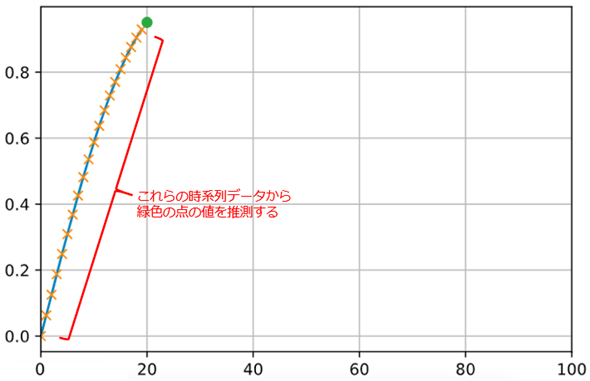
上の図は、ある時刻tにおけるsin関数(正弦関数)の値をグラフにプロットしたものです。グラフの×はサイン波の1周期を50分割して、それらの各地点(各時刻)におけるsin関数の値(sin(t)の値)を示しています。ここで重要なのは、立ち上がり(t=0の近辺)の時点では変化が大きく、極大値の1へとsin関数の値が近づくにつれて、その変化は少なくなっていく点です。そして、極大値から極小値である-1へと値が変化する際には、極大値付近での値の変化は少なく、それがしだいに大きくなってから、極小値に近づくにつれてまた小さくなっています。サイン波は-1と1の間を振動しますが、今述べたような数値変化が繰り返されていきます。
sin関数で計算されるこれらの値「だけ」を与えられたときに、人がそのデータをグラフにプロットしてみれば、「これはサイン波だね」と瞬間的に判断できるでしょう。しかし、コンピューターにこれを与えたときに、すぐにそれをサイン波と理解して、その波形がどんなものかを推測できるようになるでしょうか。この問題を解くには幾つかの手法が考えられますが、今回はサイン波の値を時系列データとして捉えて、RNNを使って取り扱ってみましょう。あまり深いところの話はせずに、取りあえずRNNに慣れることを目的としています(今回の内容はこのノートブックで公開しているので、必要に応じて参照してください)。
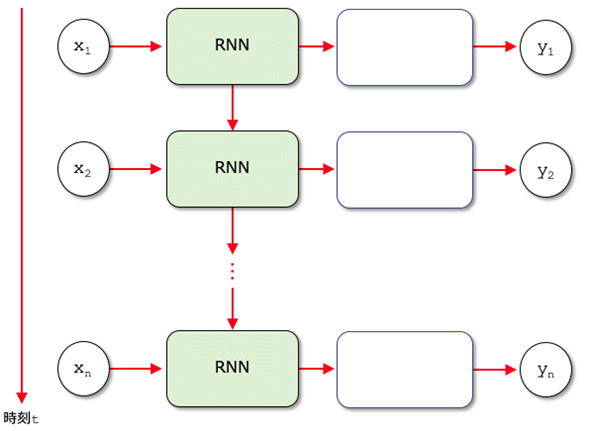
RNNの振る舞いはよく次のような図で示されます。
この図では、x1〜xnがRNN層へ(時刻の経過に従って)入力されています。RNNは入力された値を処理しますが、このときRNN層から2つの矢印が出ている点に注目してください。1つは次の層(本稿では全結合層)への入力となっていますが、もう1つは次(の時刻の)データを処理するRNN層への入力となっています。前回までに見てきたニューラルネットワークとは異なり、このようにある入力の処理結果が次の入力の処理結果に関与するようにすることで、RNNでは時系列データが持つ関係性を計算に組み込もうとしているというわけです。
この処理は「隠れ状態」などと呼ばれるオブジェクトを用いて実現しています。
RNNを使ってサイン波を推測/プロットするための準備
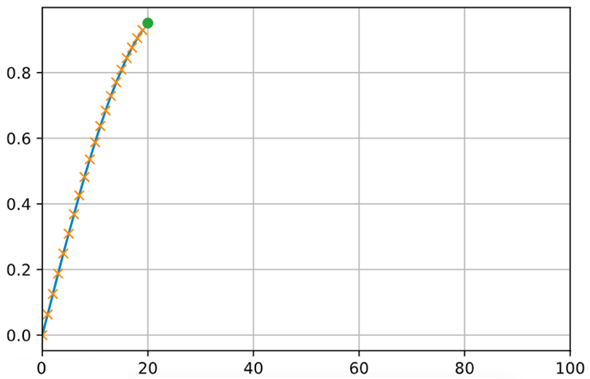
今回は、以下のグラフの×で表された連続するデータを時系列に沿ったひとかたまりのデータ(バッチ)として、バッチごとに次の値(以下のグラフの緑色の点)を正解ラベルとするような訓練データを作成して、RNNに「ある連続する値が入力されたら、次の値はコレになる」ということを学習させることを目的としています。そうすることで、ニューラルネットワークが、sin関数がどんなものであるかを知らなくとも、それと同様な値を推測できるようになるでしょう。そうなれば、推測値からサイン波をプロットできるようになるはずです。
サイン波の値を格納するデータは次のようにして作成します。
import numpy as np
import matplotlib.pyplot as plt
import torch
from random import uniform
def make_data(num_div, cycles, offset=0):
step = 2 * np.pi / num_div
res0 = [np.sin(step * i + offset) for i in range(num_div * cycles + 1)]
res1 = [np.sin(step * i + offset) + uniform(-0.02, 0.02) for i in range(num_div * cycles + 1)]
return res0, res1
num_div = 100
cycles = 1
sample_data, sample_data_w_noise = make_data(num_div, cycles)
このmake_data関数は、num_div/cycles/offsetの3つのパラメーターを取ります。num_divは1周期を何分割するかを、cyclesは周期の数を指定するものです。最後のoffsetはX軸(時刻)に対するオフセットを指定するものです(本稿の最後でこれを使ってみます)。range関数の引数で最後に1を足しているのは、その方が周期最後のデータがうまくはまったからで、それ以上の意味はありません。
関数内部では2つのリストを生成していますが(リスト内包表記部分)、1つはノイズを含まないキレイなサイン波となるような値を、もう1つはノイズを含めたサイン波となる値を格納します。正解ラベルの値については、ノイズを含まないサイン波を基にしたいので、少々汚いコードになっていますが、このようにしています。
実際にこの関数を呼び出して、データを作成して、グラフをプロットしてみましょう。
num_div = 100
cycles = 2
sample_data, sample_data_w_noise = make_data(num_div, cycles)
plt.plot(sample_data_w_noise)
plt.grid()
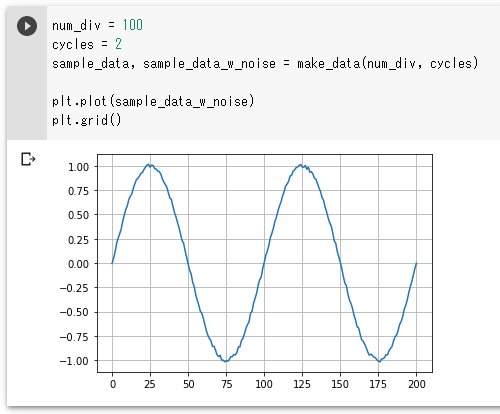
ここではノイズ付きのデータをプロットしました。実行結果を以下に示します。
ガビガビのグラフがプロットされましたね。ただし、このデータにはさらに手を加える必要があります。先ほどの図を以下に再掲しますが、必要なのは、ひとかたまりの時系列データとそれに対応する正解ラベルだからです。
make_data関数で作成する値を基に、訓練データと正解ラベルを生成する関数のコードを以下に示します。
def make_train_data(num_div, cycles, num_batch, offset=0):
x, x_w_noise = make_data(num_div, cycles, offset)
data, labels = [], []
count = len(x) - num_batch
data = [x_w_noise[idx:idx+num_batch] for idx in range(count)]
labels = [x[idx+num_batch] for idx in range(count)]
num_items = len(data)
train_data = torch.tensor(data, dtype=torch.float)
train_data = train_data.reshape(num_items, num_batch, -1)
train_labels = torch.tensor(labels, dtype=torch.float)
train_labels = train_labels.reshape(num_items, -1)
return train_data, train_labels
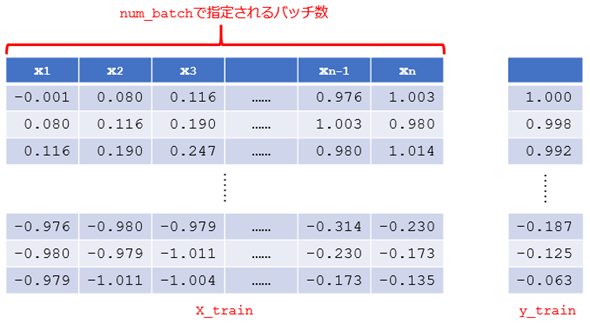
make_train_data関数では、先ほどの関数を呼び出した上で、生成されたデータを基に次のような訓練データと正解ラベルを生成します(以下の図では前者をX_train、後者をy_trainとしています)。
上のX_trainの表では、先ほどのRNNの振る舞いの図との関連が分かりやすくなるように、タイトル行にx1などの添字を足していますが、実際にはX_train[0]のようにアクセスすることには気を付けてください。もう一つ、注目する点としては、上のデータと下のデータの関係です。例えば、一番上の行のx2の値は、2行目のx1の値となっています。このように、make_data関数で作成した時系列データからnum_batchパラメーターに指定された数だけのスライスを、少しずつずらしながら、まとめたのが訓練データです。y_trainは、これらの値の次の値を表す正解ラベルになります。
ひとかたまりの時系列データを何個にするかは、num_batchパラメーターで指定します。他のパラメーターに受け取った値はそのままmake_data関数へと渡しているだけです。そして、make_data関数から返される2つのリスト(ノイズなし、ノイズあり)を使用して、上の図に示したような「リストのリスト」と「正解ラベルを要素とするリスト」を生成しています。
torch.tensor関数でリストをテンソルに変換した後に、その形状をreshapeメソッドで変更しているのは、PyTorchのRNNオブジェクトに渡せるようにしているためです(詳しくは後続の回で取り上げる予定です)。これにより、ニューラルネットワークに入力する訓練データは「バッチの個数×バッチのサイズ×1」という3次元のテンソルに、正解ラベルは「バッチの個数×1」という形状のテンソルになります。試しに実際にこれらを作ってみましょう。
X_train, y_train = make_train_data(num_div, cycles, 25)
print(X_train.shape, y_train.shape)
ここではバッチサイズ(ひとかたまりの時系列データの個数)は25としました。実行結果を以下に示します。
これでデータの準備は完了です。次にRNNを使用したニューラルネットワーククラスを定義します。
Copyright© Digital Advantage Corp. All Rights Reserved.