［AI・機械学習の数学］ベクトルの基本と類似度の計算：AI・機械学習の数学入門（2/4 ページ）

機械学習では、普通、多くの変数や係数を同時に取り扱う。そのような場合にそれぞれの変数や係数を別々に取り扱うと数式が煩雑になってしまう。ベクトルや行列を利用すれば、複数の値をひとまとめにして取り扱えるので、数式が極めて簡潔になる。今回はベクトルについて、基本的な計算方法を紹介する。

[羽山博，著]

目標【その2】： ベクトルの定数倍と和の計算

　ベクトルの定数倍（スカラー倍）と和の公式は以下の通りです。

p＝(x₁,y₁)、q＝(x₂,y₂)とし、aを定数（スカラー）とすると、

　ベクトルの差は、和の公式の＋を−に変えるだけです。つまり、以下のようになります。

解説【その2】： ベクトルの定数倍と和・差の計算

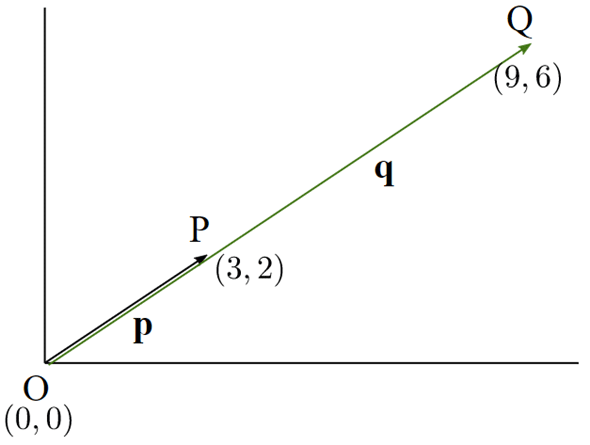
　ベクトルの定数倍というのは、ベクトルの長さを定数倍することにほかなりません。図形で表すと以下のようになります。

図2　ベクトルの定数倍

　上の図では、p＝(3, 2)を3倍しています。それをqとすると、その成分は以下のように計算されます。

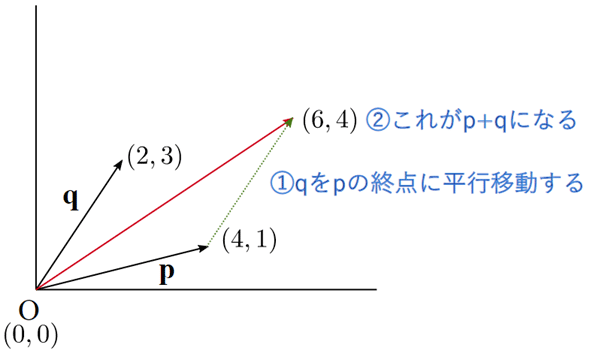
　ベクトルの和も図形で表してみましょう。

図3　ベクトルの和

　この例では、p＝(4, 1)、q＝(2, 3)として、p＋qを求めています。結果は(6,4)となります。これは、qを平行移動して、pの終点につないだもの（緑色の点線）と考えれば納得できると思います。

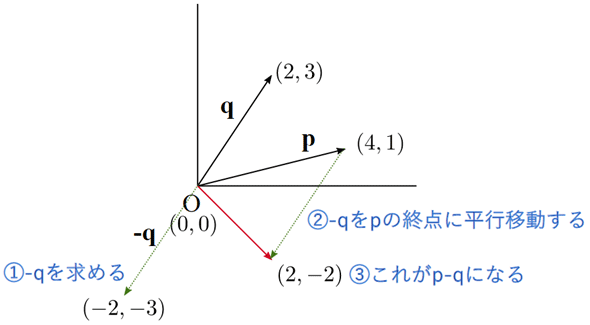
　ベクトルの差についても同様です。p−qであれば、−q、つまり(−2,−3)を足すと考えればいいですね。これも一応、図にしておきます。

図4　ベクトルの差

　ベクトルの定数倍もベクトルの和や差も、成分ごとに掛け算をしたり足し算や引き算をしたりするだけのことです。これは次元が増えても同じなので、図形的に表現できなくても、数式として操作するのは簡単です。上の例でも、いちいち図として表現するより、ルールに従って数式として操作した方が単純ですね。

　さて、これまでベクトルの計算方法について見てきましたが、重要なことは、成分ごとに計算すればいいということではなく、むしろその逆です。つまり、値を個別に扱うなら、成分ごとに計算しなければならないものを、例えば、

のように簡単に表せるということです。大事なことなので繰り返して言いますが、

や

という計算をする代わりに、例えば、

だけで表せる、というのがベクトルの便利なところなのです（次元がいくら増えてもこれだけで表せます！）。成分の計算は簡単なルールでできてしまうので、いくつかの値をベクトルとして表すことができれば、あとの計算はPCに任せてしまえばいいということです。ただ、ここでは理解を深めるために成分の計算を手計算でやってみようというわけです。