［AI・機械学習の数学］ベクトルの基本と類似度の計算：AI・機械学習の数学入門（3/4 ページ）

機械学習では、普通、多くの変数や係数を同時に取り扱う。そのような場合にそれぞれの変数や係数を別々に取り扱うと数式が煩雑になってしまう。ベクトルや行列を利用すれば、複数の値をひとまとめにして取り扱えるので、数式が極めて簡潔になる。今回はベクトルについて、基本的な計算方法を紹介する。

[羽山博，著]

目標【その3】： ベクトルの内積を求める

　ベクトルの内積は「・」を使って表します。内積を求めるための公式は以下の通りです。ただし、以下の式のxやyはただの変数名です。x軸とかy軸といった座標軸の名前ではありません。

のとき、pとqの内積p ⋅ qは以下のように計算されます。

　つまり、内積は成分ごとの積の和となります。これは次元が多くなっても同じです。一般的に表すと、

のとき、これらの内積の計算式は以下のように表現できます。

　ベクトル同士の内積の値はスカラーになることに注意してください。

解説【その3】： ベクトルの内積を求める

　内積とは何か、というのを一言で説明するのは難しいのですが、ベクトル同士の類似度（コサイン類似度）を表す基として使われる値とでも位置付けることができます。後で具体的に類似度を求める計算をしますが、そのときに内積が大きな役割を果たすことが分かります。

　ともあれ、ここでは、内積の計算に慣れておきましょう。まずは簡単な例を示します。

として、上の公式を当てはめて内積を求めてみましょう。

となります。掛け算と足し算だけなので簡単ですね。少しだけ練習問題もやっておきましょう。練習問題の（2）と（3）については、深い意味があるので、答えを確認するだけでなく解説もぜひ読んでみてください。動画での解説も用意しておくのでぜひ参考にしてください。

動画1　「ベクトルの内積」の練習問題

練習問題

（1） (1,2,3)と(4,5,6)の内積を求めてみましょう。

（2） 以下の内積をそれぞれ求めてみましょう。
　　a. (1,0)と(1,0)
　　b. (1,0)と(0,1)
　　c. (1,0)と(−1,0)

（3） w＝(−0.5,−0.5)、x＝(x₁,x₂)、b＝0.8のとき、w⋅ x＋bの値を求めてみましょう。

練習問題の解答

　練習問題の解答を穴埋め方式で記します。オレンジ色の部分をクリックまたはタップすると答えが表示されるので、考えながら読み進めていってください。

（1） 成分ごと積を求め、全て足せば求められます。

(1,2,3) ⋅ (4,5,6) ＝ 1 ⋅ 　4　 ＋ 2 ⋅ 5 ＋ 　3　 ⋅ 6
　 　　　　　　　＝　4　＋10＋　18　
　 　　　　　　　＝32

（2） やはり成分ごとの積和です。

a. (1,0) ⋅ (1,0) ＝ 1 ⋅ 　1　 ＋ 　0　 ⋅ 0
　 　　　　　　＝　1　＋ 0
　 　　　　　　＝1

b. (1,0) ⋅ (0,1) ＝ 1 ⋅ 　0　 ＋ 0 ⋅ 　1　
　 　　　　　　＝　0　＋ 0
　 　　　　　　＝0

c. (1,0) ⋅ (-1,0) ＝ 1 ⋅ 　−1　 ＋ 0 ⋅ 0
　 　　　　　　＝　−1　＋ 0
　 　　　　　　＝−1

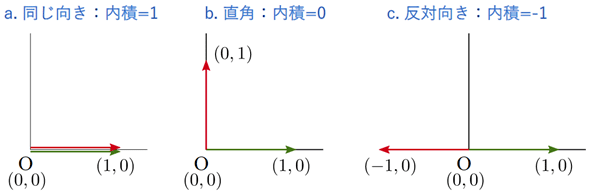
　a／b／cで見たベクトルを図で表すと以下のようになります。いずれもベクトルの大きさ（長さ）は1です。

図5　ベクトル同士の関係と内積

　ベクトルの大きさを1にそろえると、内積がベクトル同士の関係を表していることに気付くと思います。

　内積が1に近い場合は、ベクトル同士が同じ向きである（似ている）ことを表しています。(1,0)と(1,0)は全く同じものなので、当然といえば当然です。

　また、内積が0に近いと、ベクトル同士が直角であることを表します。この場合、2つのベクトルは「似ていない」と考えていいでしょう。(1,0)と(0,1)の各成分には何も共通点がないですね。

　さらに、内積が-1に近いと、ベクトル同士が反対を向いていることが分かります。正反対ということなので、いわば「似てはいるが向きが逆」と捉えられます。(-1,0)と(1,0)なら、各成分の絶対値は等しいので、その点においては「似ている」ともいえますね。

　実は、これらの値（1／0／-1）は2つのベクトルがなす角のコサイン（cos）の値になっており、これがコサイン類似度と呼ばれるものです。ただし、内積がそのままコサイン類似度になるわけではありません。この例では、大きさが1のベクトル（単位ベクトル）同士だったので、そのままコサイン類似度が求められただけです。大きさが異なる場合には、向きを変えずに大きさを1にそろえてあげればいいのですが、それについては後ほど説明します。

（3） これも公式をそのまま適用するだけです。数値の計算は必要ではないので、公式を適用して終わりです。

　w＝(−0.5,−0.5)、x＝(x₁,x₂)、b＝0.8なので、

w ⋅ x ＋ b ＝ 　−0.5　 ⋅ x₁ − 0.5 ⋅ 　x₂　 ＋ 　0.8　

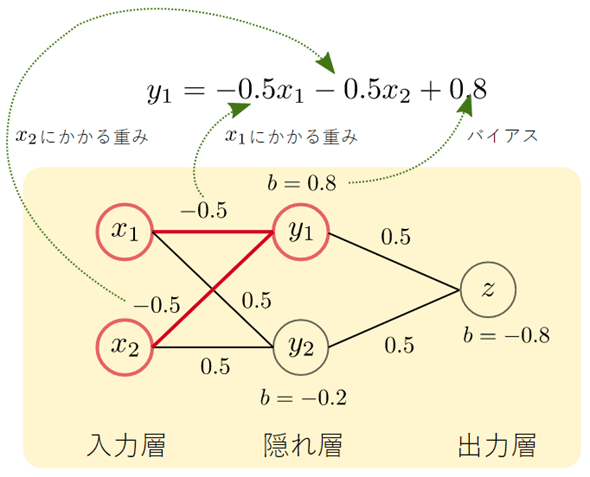
となります。実は、この式は前回見たニューラルネットワークの一部を表しています。wが重みを表すベクトル、xが入力層の値で、bがバイアスです。

図6　ニューラルネットワークの例

　前回は、y1へに入力される値を表す式を、

と表しました。重みの-0.5をw1やw2という文字、バイアスの0.8をbという文字で表すと、

のような形になりますが、ベクトルを使えば、

と、簡単に表せることが分かります。変数と重みが多くなると［A］式はどんどん複雑になりますが、［B］式はまったく変わりません*2。

*2　この例では、1つの式でニューラルネットワークの一部しか表せませんが、さらに「行列」を利用するとニューラルネットワークの各層を1つの式で表せるようになります。

　最後に、ベクトルの大きさについて見るとともに、任意のベクトルについてコサイン類似度を求める方法を見ておきましょう。