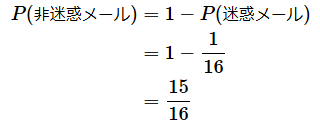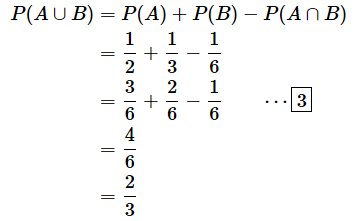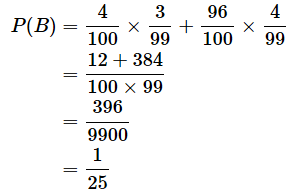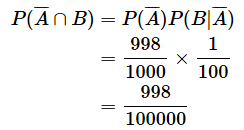[AI・機械学習の数学]確率の基本から条件付き確率までをおさらいしよう:AI・機械学習の数学入門
分類や推定、予測など、機械学習のさまざまな手法の基礎をなす確率/統計の基本として、確率の表し方、和事象/積事象/排反事象、独立と従属、条件付き確率をおさらいする。
確率という言葉は、微分やベクトルなどとは異なり日常生活でもよく使われる言葉です。しかし、その割に、何だかよく分からないという印象を持っている人も多いようです。感覚的に理解できるというのがかえってアダになっているのかもしれませんね。
そこで、今回は確率をきちんとおさらいします。その上で次回は、機械学習の基礎として幅広く利用されているベイズの定理についての理解を深めていきたいと思います。具体的には、今回と次回で以下のようなトピックを扱います。
用語だけを見ると何だか難しそうに思えるかもしれませんが、結局のところ、やはり四則演算だけで全て計算できてしまいます。というわけで、簡単な例から一つ一つ見ていきましょう。なお次々回は、「分布」を中心に統計について取り上げます。
目標【その1】: 確率の表し方
ある事象をAと表したとき、その事象が起こる確率をP(A)と表します。例えば、どの目も同じように出る6面体のサイコロを振ったときに、1が出る事象をAとしたとき、その確率は1/6なので、以下のように表されます。「P」は「Probability(確率)」の頭文字です。
それぞれの事象をAiと一般的に表すと、それらの確率は、
となります。サイコロの場合、Aiは{1,2,3,4,5,6}のいずれかになります。なお、全ての事象の確率の総和は1になります。
また、ある事象Aが起こらないという事象のことを余事象と呼び、
と表します。全ての事象の確率を足すと1になるので、以下の関係が成り立ちます。
解説【その1】: 確率の表し方
コインを投げる、サイコロを振る、などの行為を試行と呼び、そのときに起こる出来事を事象と呼びます。堅苦しい用語を使っていますが、それぞれ「何かをやること」「できごと」と考えれば身近に感じられると思います。
確率とは、ある事象が起こる「確からしさ」を表した値です。具体的には、その事象が起こる数を全ての事象が起こる数で割ったものです。なお、全ての事象は全事象と呼ばれます。
事象が起こる数というのは、もう少し正確に言うと「場合の数」なのですが、要するにその事象には何通りの起こり方があるか、ということです。
例えば、どの目も同じように出る6面体のサイコロで考えてみましょう。
- 試行 …… サイコロを振ること
- 全事象 …… サイコロの目は{1,2,3,4,5,6}の6通り
ですね。このとき、サイコロの目「1」が出るという事象は{1}の1通りなので、その確率は、
となるわけです。従って、300回サイコロを振ると、サイコロの目「1」は300×(1/6)=50回出るであろうと考えられます。もちろん、実際にサイコロを振ると、300回のうちぴったり50回(全体の1/6)ではなく48回しか「1」が出なかったとか、53回も「1」が出たということもあるでしょうが、理想的なサイコロを何度も振ると、「1」の出る回数が全体の1/6に限りなく近づいていくということです(このことを大数の法則と呼びます)。
念のため、穴埋め問題で確認しておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます。サイコロの例では、偶数の目が出る事象は{2,4, 6 }の 3 通り なので、その確率は、
偶数の目 が出る事象の数
P(偶数) = ─────────────
全事象 の数
3 1
= ─── = ───
6 2
となります。簡単でしたね。なお、ある事象が全く起こらないとき(サイコロで「7」の目が出るなど)の確率は0で、その事象が必ず起こるとき(サイコロの「1」〜「6」のいずれかの目が出るなど)の確率は1です。「私がそんなことをする確率は2万パーセントない」などという言い方がありますが、確率は0以上1以下の値を取り、確率が1である(つまり、何らかの事象が必ず発生する)ことを100%(パーセント)とするので、2万パーセントというのは、強調したい気持ちは分かりますが、数学的には誤った表現です(2万パーセントでは、確率が200になってしまいますが、今述べた通り、確率は0以上1以下の値しか取りません)。
さて、このあたりは初歩の初歩ですが、ちょっと違った例も見ておきましょう。受信した160通の電子メールのうち10通が迷惑メールであったとします。このとき、迷惑メールである確率は、目的の事象が10、全事象が160なので、
となります。非迷惑メールである確率は、迷惑メールの余事象なので、
となります。
ところで、最初に見たサイコロの例と今の迷惑メールの例では違うところがあることに気が付いたでしょうか。サイコロの例は実際にサイコロを振ったわけではなく、理想的な場合の値です。一方、迷惑メールの例は実際の試行から推定した確率です。これらをきちんと区別する場合、前者のような確率を数学的確率と呼び、後者のような確率のことを統計的確率と呼びます*1。
*1 中学や高校の数学で、場合の数や確率に苦手意識を持っていた人も多いのではないでしょうか。かくいう著者もその一人です。その理由の一つがコイン投げやサイコロ、壺(つぼ)に入った赤玉・白玉といった例でした。人生の中で赤玉や白玉を取り出すことなんてありっこないよ、とモチベーションが全く上がらなかったのでした。が、今から考えると、それらは話を簡単にするためで、かといって、あまりに抽象化しすぎると実感が湧かないので、ある程度の具体性を持たせるという配慮(苦肉の策かもしれませんね)であったということに思いが至らなかっただけなのでした。
いずれにせよ、確率の基本は、事象の数を「数え上げること」です。では、次に和事象や積事象などの確率についても見ていきましょう。
目標【その2】: 和事象・積事象、排反事象
事象Aと事象Bの少なくともいずれか一つに当てはまる事象のことを和事象と呼び、∪という記号を使ってA∪Bと表します。∪はコップのような形なのでコップ……ではなくちょっと気取ってカップ(CUP)と読みます。つまり「エー・カップ・ビー」ですね。そして、A∪Bの確率を、
と表します。
一方、事象Aと事象Bの両方に当てはまる事象のことを積事象と呼び、∩という記号を使ってA∩Bと表します。∩は帽子のような形なのでキャップ(CAP)と読みます。つまり「エー・キャップ・ビー」となります。A∩Bの確率は、
と表します。P(A)、P(B)、P(A∪B)、P(A∩B)の関係は以下の公式で表されます。というと、何やら難しい公式を覚えなければいけない気分になるかもしれませんが、この公式は覚えるほどではない当たり前のことを表しているだけです。解説のところでベン図を見ると、[1]は簡単に理解できます。
排反事象とは、事象Aが起こるときには事象Bは起こらないし、事象Bが起こるときには事象Aが起こらないということです。事象Aと事象Bの両方に当てはまる事象が起こることはないので、P(A∩B)=0になります。これも後述のベン図を見れば明らかです。
ここで示した式以外にも幾つかの公式がありますが、それらについては上の公式から導き出せるので、具体例で見ていきましょう。
解説【その2】: 和事象・積事象、排反事象
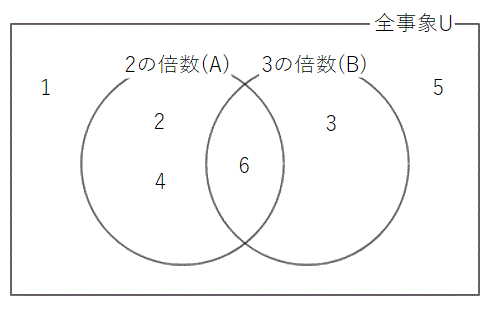
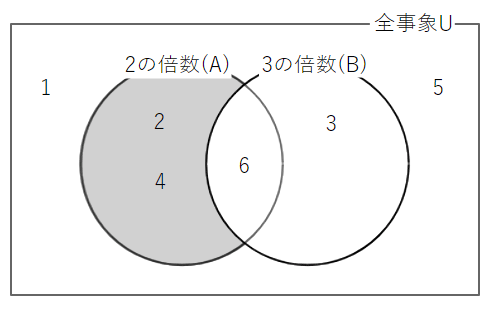
目標のところに記した式を具体例で確かめていきましょう。話を簡単にするためにサイコロを使いますね。事象Aを「2の倍数が出る」とし、事象Bを「3の倍数が出る」としましょう。これらを小学校のときに習ったベン図で表すと以下のようになります。
確率を求める前に、まず、図を見ながら事象の数を数え上げてみましょう。これは穴埋め問題にしておきます。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
A = {2,4, 6 }
B = { 3 ,6}
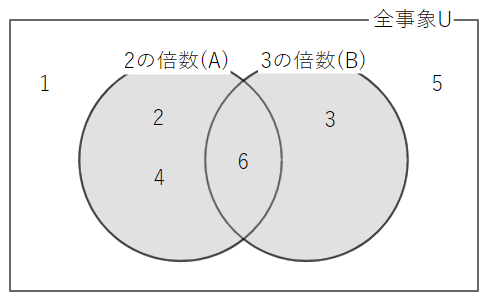
となります。Aは3通り、Bは2通りです。続いて、和事象と積事象についても数え上げていきましょう。以下のベン図に示されたアミカケの部分が和事象と積事象を表すので、図を見ながら答えると簡単です。まず、和事象からです。いずれかの輪の中にあるものが和事象ですね。
A∪B = {2, 3 ,4, 6 }
となるので、A∪Bは4通りです。
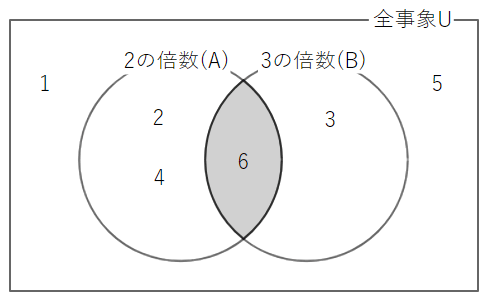
一方、積事象は、両方の輪の交わった部分で表されます。
A∩B = { 6 }
となるので、A∩Bは1通りであることが分かりました。
次に、それぞれの確率を求めてみます。全事象は6通りなので、以下のようになります。
3 1
P(A) = ─── = ───
6 2
2 1
P(B) = ─── = ───
6 3
4 2
P(A∪B) = ─── = ─── … [2]
6 3
1
P(A∩B) = ───
6
目標のところに記した公式([1]式)が成り立っているかどうか確認してみましょう。
となり、数え上げて求めた[2]式の結果と一致しています。
くどくなりますが、ベン図をもう一度見てみると、以下のようなことが分かります。
- Aは{2,4,6}の3個、Bは{3,6}の2個
- AとBをそのまま並べると{2,4,6,3,6}となり、A∩Bである{6}が重複する
- 従って、A∪Bの個数を求めるためには、Aの個数とBの個数を足し、そこからA∩Bの個数を引けばよい
全事象は6通りなので、P(A∪B)は、
となります。[3]を見れば分かりますが、分母は全て全事象の数の6なので、事象の個数を数え上げなくても、確率が分かっていれば同様の計算ができるというわけです。
さて、目標の公式を変形すると、さまざまな確率が求められます。例えば、サイコロの目が2の倍数であって3の倍数でない場合は、ベン図で表すと以下のグレーの部分になり、その確率は、事象の個数を数え上げれば2/6=1/3であることがすぐに分かりますが、式を変形すれば個数を数えなくても求められます。
グレーの部分の確率を式で表すと、
となります。
なので、それをそのまま式で表しただけです。ベン図を見ると、この確率がP(A)−P(A∩B)とも表されることが分かります。そこで、[1]式を変形します。
P(B)を左辺に移項した後、左辺と右辺を入れ替えただけです。右辺を計算してみましょう。
確かに答えが合っていますね。
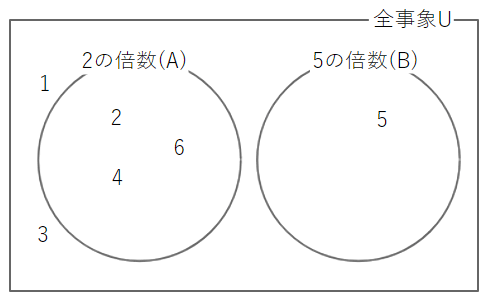
排反事象は簡単です。例えば、サイコロの目が2の倍数である事象と5の倍数である事象の両方に当てはまる事象はないので排反です。もちろん、P(2の倍数∩5の倍数)は0です。
サイコロばかりではつまらないので、少し思いを巡らせて、身近な例を自分で考えてみましょう。……いかがでしょう。例えば、ある時間に、A氏がキッチンでつまみ食いしたという事象と、A氏が熟睡していて寝室から出なかったという事象は排反ですね(数学は「構造」の学問だといわれることがありますが、同じ構造を持つ具体例をいろいろと考えたり、逆に、さまざまな具体例がどのような構造になっているのかを考えたりすれば、理解が深まります)。
さて、これまでは基本的に1回の試行での確率について見てきました。ここからは複数試行の場合についても考えてみましょう。
目標【その3】: 独立と従属、条件付き確率
ある試行の結果が別の試行に何ら影響を及ぼさないことを独立と呼びます。例えば、サイコロを1回振るという試行ともう1回振るという試行の結果は独立事象です。2回目にどの目が出るかは、1回目にどの目が出たかということとは無関係だからです。事象Aと事象Bが独立の場合、両方の事象が起こる確率は、
のようにそれぞれの確率の積で表されます。
一方、ある試行の結果が別の試行に影響を及ぼすことを従属と呼びます。例えば、福引の例がそれに該当します。アタリが何本かあり、1回目にアタリが出たときに2回目にアタリが出る確率と、1回目にハズレが出たときに2回目にアタリが出る確率は異なります。つまり、ある試行の結果が別の試行に影響を及ぼすわけです。
このような場合、事象Aが起こったときに事象Bが起こる確率は、
と表されます。あとでも触れますが、|は「ギブン(given)」と読みます。つまり、「ピー、ビー、ギブン、エー」と読みます。
このような確率を条件付き確率と呼びます。P(B|A)は、高校の数学ではPA(B)と表されることもありますが、機械学習ではP(B|A)の方が一般的な表し方です。
既に見たように、事象Aと事象Bが共に起こる確率はP(A∩B)ですが、これは「事象Aが起こる確率」×「事象Aが起こったときに事象Bが起こる確率」なので、
となります。この式は条件付き確率の乗法公式と呼ばれる公式で、機械学習でよく使われる「ベイズの定理」(次回解説)の基礎となっています。以降、単に「乗法公式」というと、この条件付き確率の乗法公式を指すものとします。また、あいまいにならない場合は、掛け算の記号は省略して、
と書くことにしますが、慣れないうちは「ここは掛けるだな」と意識しながら読むようにするといいでしょう。
P(A)≠ 0 の場合、乗法公式は以下のように変形できます。
解説【その3】: 独立と従属、条件付き確率
「独立」に関しては、具体的な例で解説しなくても容易に理解できると思います。とはいえ、私たちの直感と異なる場合もあるので注意が必要です。例えば、全ての目が同じように出る理想的なサイコロを5回振って{1,4,2,6,3}が出る確率と{1,1,1,1,1}が出る確率は、それぞれの試行が独立なので、いずれも、
となり、等しくなります。しかし、私たちの直感では、サイコロの目が{1,1,1,1,1}と続くことは「まれ」にしか出ないような気がするので確率が小さく、{1,4,2,6,3}のように不連続に続く方が「ありふれている」ような気がするので確率が大きいと思いがちですが、これは認知の歪(ゆが)み(認知バイアス)によるものです。
次に、事象が「従属」である場合について見てみましょう。ここからは動画でも解説しているので、苦手意識のある人はぜひ参照してみてください。
動画1 条件付き確率
目標のところに記したように、事象Aが起こったときに事象Bが起こる確率を以下のように表しました。
まずは、この式の書き方を確実に身に付けておきましょう。求める確率はあくまでも事象Bが起こる確率なので、Bを最初に書くと考えれば納得がいくでしょう*2。
*2 「簡単な確率は分かるけど、条件付き確率はややこしくて」と、このあたりで確率につまずいてしまう人はけっこう多いようです(実は筆者もその一人でした)。それは、P(B|A)という書き方に慣れていないせいかもしれません。日本語だと「事象Aが起こったときに」という条件を先に言うので、書き方と順序が逆になっています。確かにちょっとややこしいですね。英語だと「probability of B given A」のような言い方なので、式の書き方と同じ順序になりますし、あくまでも事象Bが起こる確率であるということも明確に分かります。分かりにくいと感じたら、英語でどう表すのかを調べてみると案外スッキリと理解できることもあります。
では、乗法公式を具体例で確認しておきましょう。話を簡単にするために、100本のうち4本のアタリがあるくじを2回引くものとします。1本目がアタリであったときに、2本目もアタリである確率を求めてみます。
1本目がアタリである確率は当然4/100、つまり1/25です。2本目については、アタリくじが既に1本引かれているので、残りは99本で、その中にアタリが3本あります。従って、その場合の2本目のアタリの確率は3/99、つまり1/33です。というわけで、1本目がアタリであるという事象をA、2本目がアタリであるという事象をBとすると、事象Aが既に起こったときに事象Bが起こる確率(条件付き確率)は、図7のようになります。
では、1本目と2本目の両方がアタリであるという事象P(A∩B)の確率はいくらになるでしょう。これは、乗法公式を使えば簡単に求められます。
となります。P(A∩B)は1本目と2本目の両方がアタリである確率です。それは、1本目がアタリである確率P(A)と、1本目がアタリであったときに2本目もアタリである確率P(B|A)の積となっています。……と日常の言葉を交えて書くと当然のことだというのが分かりますね。しかし、いちいち日常の言葉を使うのが面倒なので、文字や記号を使った式で簡潔に表しているだけのことです*3。
もちろん、「条件付き確率P(B|A)」は「事象Bのみが起こる確率P(B)」とは異なります。P(B)は、「2本目がアタリ」のみが起こる確率なので、1本目がアタリで2本目がアタリ、1本目がハズレで2本目がアタリの確率の和になります。よって、
です。つまり、1回目にくじを引いても、2回目にくじを引いても当たる確率は同じです。が、1回目の結果を見てからだと、2回目に当たる確率は変わるというわけです。
*3 「1本目と2本目の両方がアタリ」というのと、「1本目がアタリであったときに2本目もアタリ」というのは、どちらにしても両方当たっているんだから、同じじゃないの?と思われるかもしれませんが、どの時点で求めた確率かということが異なります。前者はくじを引く前に考えられるアタリかハズレかの全ての事象が全事象です。一方、後者は、1本目が既に当たっている場合が全事象で、そのような状況で2本目が当たる確率という意味です。
条件付き確率は重要なので、練習問題を通して別の例も見ておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます(※編集部注:余事象を表す「文字のオーバーライン」は本稿のテキスト文では「Ā」「B̄」のようにBでは分離されて表示されますので、ご了承ください。適宜、読み替えてください)。
練習問題:
あるウイルスに感染していることを事象Aとし、検査で陽性になることを事象Bとします。以下のような事象の確率を式で表してみてください。
1. ウイルスに感染していることが既に分かっていて、検査で陽性になる確率 …… P( B|A )
2. ウイルスに感染していることが既に分かっていて、検査で陰性になる確率 …… P( B̄|A )
3. ウイルスに感染しており、かつ、検査で陽性になる確率 …… P( A∩B )
4. ウイルスに感染しており、かつ、検査で陰性になる確率 …… P( A∩B̄ )
練習問題の解答:
1. ウイルスに感染しているという事象がA、陽性になるという事象がBなので、Aであるという条件の下でBが起こる確率ということですね。従って、P(B|A)となります。確実に理解し、式の書き方に慣れるためにもう一度確認しておきましょう。
2. 陰性であることがP(B̄)で表されるので、P(B̄|A)ですね
3. AかつBである確率なのでP(A∩B)です。P(B∩A)でも構いません
4. Aかつ(Bでない)なので、P(A∩B̄)となります。P(B̄∩A)でも構いません
次に、具体的な例について考えてみます。ここも穴埋め問題にしてあるので、答えを考えながら読み進めてください。以下のことが分かっているものとしましょう。やはり、オレンジ色の部分をクリックまたはタップすると答えが表示されます。なお、ここからは動画でも解説しているので、ぜひ参照してみてください。
動画2 条件付き確率の具体例
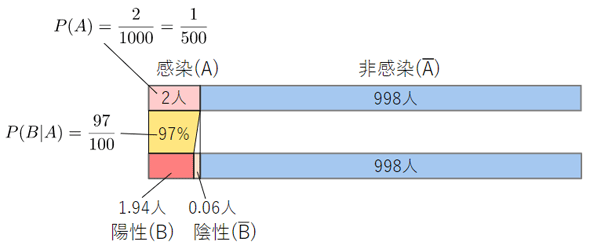
例えば、以下のようなことが分かっているものとします。
- ウイルスに感染している人は1000人中2人である
- ウイルスに感染していることが既に分かっている人が、検査で陽性になる確率は97%である
上記の確率を式で表すと、
2 1
P(A) = ──── = ────
1000 500
97
P(B|A) = ────
100
となりますね。条件付き確率では、条件に当てはまった事象が全事象となることに注意してください。97%というのは全ての人の97%ではなく、感染していることが分かっている人のうちの97%ということです。
では、このとき、感染者であり、かつ陽性となる人は1000人中何人いるでしょうか。乗法公式を使って、感染者であり、かつ陽性となる確率P(A∩B)を求めてみましょう。
P(A∩B) = P(A)P( B | A )
1 97
= ─── × ───
500 100
97
= ───────
50000
= 0.00194
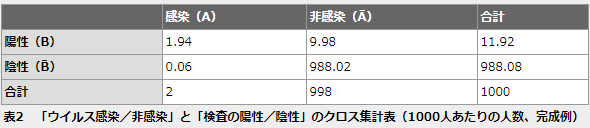
ということで、0.194%です。つまり、1000人中1.94人が感染していて検査の結果も陽性になるということです。これまでのお話を図10で確認しておきましょう。
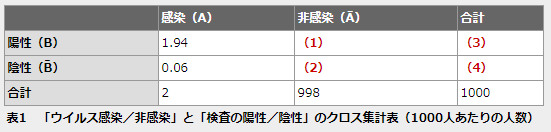
さらに、これまでに得られた情報を表にまとめておくと表1のようになります。表の中の値は確率ではなく人数であることに注意してください。1.94という数字は感染者で、かつ陽性である人数(A∩Bの人数)でしたね。条件付き確率の97%というのは1.94÷2で求められることも分かりますね。
(1)〜(4)に関してはまだ値を示していませんが、これらのうち1つでも分かれば、残りの部分も埋められます。乗法公式の計算練習も兼ねて、表を埋めてみましょう。例えば、
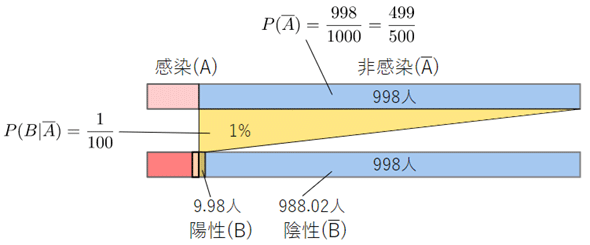
- ウイルスに感染していないことが既に分かっている人が、検査で陽性になる確率は1%である
であったとしましょう。この確率は、
と表されます。
さて、(1)は非感染でかつ陽性である人数ですが、その確率P(Ā∩B)は、乗法公式を使って、以下のように求められます。
を書いただけです。
これについても、図11で確認しておきましょう。
表1には1000人あたりの人数が記入されているので、表1の(1)には、1000×998/100000=9.98が入ることが分かります(そもそも、非感染者998人のうちの1%なので、9.98人であることは暗算でも求められますが、乗法公式の検算ができたということでヨシとしましょう)。
表1の(2)〜(4)も埋めると表2のようにまとめられます。縦横の合計もきちんと合っていますね。
この表ができれば、ベイズの定理により、検査で陽性であったときにウイルスに感染している確率P(A|B)を求めることができるようになります。そこで……と言いたいところですが、今回は条件付き確率をしっかりと理解することに主眼を置きたいので、ベイズの定理については次回見ていくこととします(答えだけ先に書いておくと、0.1628(=約16.3%)です。以外に小さな値だと思われるかもしれませんが、図11を見れば、非感染者が圧倒的に多く、非感染者の中でも陽性になる人が9.98人いることなどから何となく納得できると思います。……が、きちんと計算して答えを求める方法は次回のお楽しみです)。
コラム 条件付き独立とは
ある条件Xのもとで起こった事象Aと事象Bが独立であることを条件付き独立と呼びます。それらの事象の両方が起こる確率は以下のように表されます。
と表されます。例えば、競馬である馬が勝ったという条件のもとで、AさんとBさんがランダムな数字を言って予想が当たったということは独立と考えられます(もっとも、この場合は条件がついていなくても独立ですが)。上の式で、事象を一般的にAiと表し、それらが全て起こることをAと表すと、
となります。∏はπの大文字で「全てを掛ける」という意味です。
次回は……
今回は、確率と統計のうち、主に確率について、その基礎について見てきました。次回は、今回の条件付き確率を踏まえて、ベイズの定理を学んでいきます。ベイズの定理と聞くだけで難しくて手に負えないと感じてしまう人もいるかもしれませんが、条件付き確率が理解できれば、もうほとんどベイズの定理も理解できたようなものです。ゆっくりと丁寧に解説しますのでご安心ください。
Copyright© Digital Advantage Corp. All Rights Reserved.