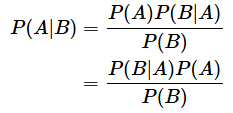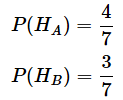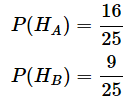[AI・機械学習の数学]機械学習でよく使われる「ベイズの定理」を理解する:AI・機械学習の数学入門
確率と統計の基本を踏まえた上で、スパムフィルターをはじめとして幅広く利用されているベイズの定理の考え方や応用について見ていく。
前回は高校で学んだ確率の基礎と条件付き確率をおさらいしました。今回は、その内容を踏まえて、機械学習の基礎として幅広く利用されているベイズの定理についての理解を深めていきたいと思います。前回と今回で取り扱っているトピックは以下の通りです。
ベイズの定理は、難しい印象のあるベイズ統計学の基礎の基礎ですが、条件付き確率の乗法公式さえ分かれば、簡単に理解できます。一歩ずつ丁寧に説明していくので、急がずにゆっくりと読み進めていってください。なお、前回の「条件付き確率」を読んでいない場合は、先に一読することをお勧めします。セットでまとめて読みやすいように、今回は各節や図、脚注などの番号は、前回の番号からの続きとなっています。
目標【その4】: ベイズの定理
まずは前回学んだ条件付き確率の乗法公式(以下、単に「乗法公式」)の復習です。「事象Aと事象Bの両方が起こる確率」は「事象Aが起こる確率」と「事象Aが起こったときに事象Bが起こる確率」の積で表されます。つまり、
と表現できましたね。この式は、機械学習でよく使われるベイズの定理の基礎となっています。これについては前回見た通りです。
ベイズの定理の基本的な形は以下の通りです。
事象Aを原因や仮説(Hypothesis)、事象Bを結果やデータ(Data)と考え、その頭文字を使って、以下のように表すこともあります(むしろ、この表し方がよく使われます)。
この式を見ると、左辺は「結果が得られたときの原因の確率」であることが分かります。右辺を計算すれば、何かの原因の確率が求められるというわけです。なお、P(H)は事前確率、P(H|D)は事後確率と呼ばれます。また、P(D|H)は尤度(ゆうど)、P(D)は周辺尤度と呼ばれます(※「尤度」の意味は後述)。これらの用語を使って上の式を書くと、以下のように表されます。
事前確率は「コトが起こる前の原因の確率」で、事後確率は「コトが起こった後に考えられる原因の確率」です。尤度の「尤」は「尤(もっと)もらしい」という意味で、P(D|H)はHという原因が分かればDという結果が得られるのは、その確率はまあもっともらしいと考えられる値だよね、といった意味合いです。英語のlikelihood(ありそうなこと、見込み)の訳ですね。周辺尤度はもう少し後で説明します。
解説【その4】: ベイズの定理
ここから乗法公式を使ってベイズの定理を導き出していきます。その方法については動画でも解説しているので、ぜひ視聴してみてください。
動画2 ベイズの定理
条件付き確率の乗法公式は、AとBを別の文字にしてももちろん成り立ちます(例えば、目標のところではDとHに書き換えた例を示しました)。そこで、AとBを入れ替えてみましょう。すると、以下のような式が成り立つことが分かります。
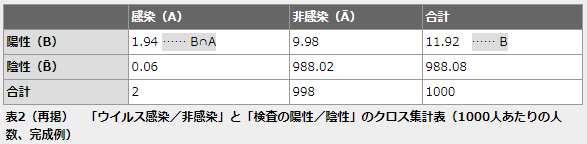
[1]式は最初に見た乗法公式で、具体的な数値を使って前回確かめました。[2]式がAとBを入れ替えたものです。「え、ホント? 何だか騙(だま)されているような気が……」という人もいるかもしれないので、ちょっと寄り道になりますが、乗法公式のおさらいも兼ねて、[2]式がちゃんと成り立っていることを具体的な数値で確認しておきましょう。以下の表は前回見たウイルスの感染/非感染と検査の陽性/陰性の人数の表です。
[2]式の左辺、つまりP(B∩A)の値は1.94/1000です。右辺は、以下の通りです。
- P(B) …… 11.92/1000 (陽性である確率)
- P(A|B) …… 1.94/11.92 (陽性であったときに感染している条件付き確率)
計算してみると、以下のようになり、ちゃんとP(B∩A)の値と一致していますね。
では、本筋の話に戻ります。通常、私たちが求めたい確率は、陽性であるときに感染している確率です。つまり、P(A|B)の確率です(上で見た例で1.94/11.92であることが既に分かってしまっていますが)。そこで、[2]式の方をP(A|B)=の形に変形してみましょう。[2]式の両辺をP(B)で割ります。ただし、P(B) ≠ 0 とします。
右辺はP(B)で約分できるので、P(A|B)だけになりますね。左辺と右辺を入れ替えると以下のようになります。
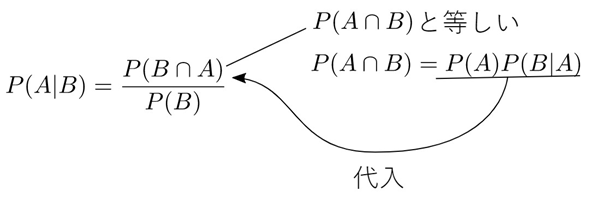
ここで、右辺の分子を見てください。Bという事象とAという事象の両方が起こることは、Aという事象とBという事象の両方が起こることと同じなので、P(B∩A)=P(A∩B) です。ということは、[1]式を代入できますね(図12)。
代入を行って、式を整理すると以下のようになります。
はい、これで目標の式が導き出されました。これがベイズの定理の基本的な形です。結果(B)が分かっているときの、原因(A)の確率がこの式で求められます。例えば、検査で陽性になったときに、ウイルスに感染している確率が求められるというわけです。
では、ウイルスの例に実際に適用してみましょう。感染しているという事象は原因と考えられ、検査で陽性になるという事象は結果と考えられるので、HとDという文字で表したいところですが、引き続きAとBを使うことにします。
ベイズの定理により、陽性になった場合にウイルスに感染している確率P(A|B)を求めてみます。ここからは穴埋めにしておくので考えながら読み進めてください。オレンジ色の部分をクリックまたはタップすれば答えが表示されます。まず、目標のところに書いた式(先ほど導き出した式)をそのまま書きましょう。
P( B|A )P( A )
P(A|B) = ────────────
P(B)
P(B|A)は「ウイルスに感染していることが既に分かっていて、検査で陽性になる確率」でしたね。前回見た通り、これは97%=0.97であることが分かっているものとします。
P(A)は感染している確率です。これも既に2/1000=0.002であることが分かっています。分母のP(B)は陽性である確率ですね。これは表2から11.92/1000=0.01192であることが分かります。
というわけで、
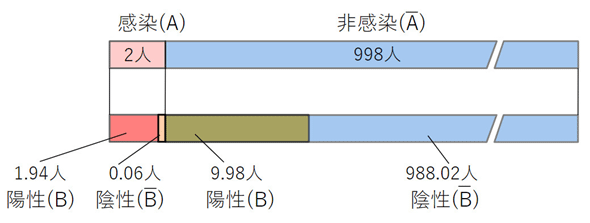
となります。検査の結果が陽性であったときに、感染している確率P(A|B)は約16.3%になります。直感的には90%を超える値が思い浮かぶかもしれませんが、意外なほどに小さい値ですね。これは、以下の図でも確認できます。
感染者よりも非感染者のほうが圧倒的に多いので、図では、非感染者の部分の幅が実際よりずいぶんと小さくなっていて、それぞれの部分の幅が比率を忠実には表していませんが、前回の図よりは多少実際のイメージに近くしてあります。ともあれ、図を見ると、陽性者全体は1.94人+9.98人=11.92人であることが分かります。そのうち、感染している人は1.94人なので、陽性者のうち、感染している人の割合は1.94÷11.92=0.1628となり、上で計算した結果と一致します。
実際のところ、表2ができていれば、図を描いたり、ベイズの定理を使って計算したりしなくても1.94÷11.92で答えは求められるのですが、ここでは、ベイズの定理が確認できたということで、ヨシとしましょう。
目標【その5】: ベイズの定理の展開
ここからは、A、Bの代わりにH、Dという文字を使うことにしましょう。単に違う文字を使うだけですが、それでも頭の切り替えが必要になるので、少しリフレッシュしてから読み進めていただくといいでしょう。
さて、ベイズの定理を一般的な表現に展開した公式は以下のようになります。以下の式のHiは原因を表すような事象Hが幾つかある場合のi番目の事象、Dは結果を表す事象です。これまでは取り扱ってきた事象が、陽性か陰性かといった2つでしたが、3つ以上になることも考えられます。そこで、式を一般化しておこうというわけです。
取りあえず、日本語でこの式の各項の説明を記しておきます。抽象的すぎて実感が湧かないかもしれませんが、今は分からなくてもあまり気にしないでください。この式を導き出す方法も含めて具体的な詳しい説明は次の解説セクションで行うので、まずは、式と以下の説明をざっと眺めておいてください。
- 左辺
- P(Hi|D) …… Dという結果が得られたときにその原因がHiである確率(事後確率)
- 右辺の分子
- P(D|Hi) …… 原因がHiであるときにDという結果が得られる確率(尤度)
- P(Hi) …… 原因がHiである確率(事前確率)
- 右辺の分母
- Σ(P(D|Hj)P(Hj)) …… 原因がHjであるときにDという結果が得られる平均的な確率(Dという結果が得られる確率、周辺尤度)
ここでの目標は、上の式を理解し、事例に適用できるようになることです。では、解説に進みましょう。
解説【その5】: ベイズの定理の展開
最初にHiやHjの意味を具体的に確認しておきましょう。実は、これまで見てきたウイルスの例では、原因となる事象が2つで排反(同時に起こらない)だったので、感染をA、非感染をĀのように簡単に表してきました。しかし、実際にはいくつもの事象がある方が普通です。その場合も、これまでの例と同様、事象は互いに排反であるものとします。
例えば、「黙読する(H1)」「音読する(H2)」「筆記する(H3)」という3つのいずれかの方法を使って、単語を記憶する実験を行うなどがそれに当たります。それらの事象に対する結果としては「合格(D1)」「不合格(D2)」などが考えられます。そこで、添字を使って一般的に表したわけです。
とはいえ、別の例で考えるとさらに頭の切り替えが必要になるので、これまでのお話の中で頭に入っているウイルスの例をそういった表し方にしてみましょう。実際にはH1、H2、H3、……のように事象が幾つかあるわけですが、話を簡単にするためにH1、H2だけで見ていこうというわけです。また、陽性がD1、陰性がD2になりますが、添字が増えると煩雑になるので、陽性のところだけを単にDと表すことにします。
なお、表の中の数値は1000人中何人かという値ではなく、確率にしておきました。
| 感染(H1) | 非感染(H2) | 合計 | |
|---|---|---|---|
| 陽性(D) | 0.00194 …… P(H1∩D) | 0.00998 …… P(H2∩D) | 0.01192 …… P(D) |
| 陰性 | 0.00006 | 0.98802 | 0.98808 |
| 合計 | 0.002 | 0.998 | 1 |
| 表3 「ウイルス感染/非感染」と「検査の陽性/陰性」のクロス集計表(数値は確率) | |||
検査の結果が陽性(D)であったときに、ウイルスに感染している(H1)確率は、P(H1|D)と表されますね。既に前項の解説【その4】でその値(P(A|B)=約16.3%)を求めましたが、ここでは、目標のところに示したベイズの展開公式が成り立つことを確認した上で、あらためてその公式を使ってP(H1|D)の値を求めてみることにします。ベイズの展開公式を導き出す方法については動画でも解説しているので、ぜひ視聴してみてください。
動画3 ベイズの定理の展開
まず、ベイズの展開公式が成り立つことを確認しましょう。H1とDという文字を使ってベイズの公式をそのまま書いてみます。
H1とH2は排反(同時に起こらない)なので、
と表すことができます。え? ちょっと何を言っているのか分からない、という人もいるかもしれませんが、以下のように、日本語で言い替えてみると、なんだ当たり前じゃん、となりますね。前掲の表3を見てもらっても明らかです。
- P(D) …… 陽性になる確率(以下の2つの和):上の例なら0.01192
- P(H1∩D) …… 感染していて、かつ陽性になる確率:上の例なら0.00194
- P(H2∩D) …… 非感染で、かつ陽性になる確率:上の例なら0.00998
[1]式の分母に[2]式の右辺を代入してみましょう。
条件付き確率の乗法公式を適用すると、分母の各項は、
と表されます。これらの右辺を[3]式の分母の各項に代入してみましょう。
分母の部分は、結局のところ「総和」なのでΣを使って表すと以下のようになります。添字としてjを使っていることに注意してください。jという文字には特に意味はありませんが、事象がH1,H2,...,Hnであれば、j=1からnまでの合計になります。
P(H1|D)などのH1の部分はH2かH3のいずれかなので、Hiと表すことにします。このiは変化するわけではなく特定の値を一般的に表しただけです。
はい、いかがでしょう。目標のところで示した式ができましたね。分母の「周辺尤度」は、表の周辺部分に現れる値とでもいったイメージで捉えておいていただいて結構かと思います(正確に言うと、対象としている尤度も含め、全ての尤度を事前確率で重み付けした期待値になっています……が、結局のところP(D)の値なので、その事象が起こる平均的な確率ということになります)。
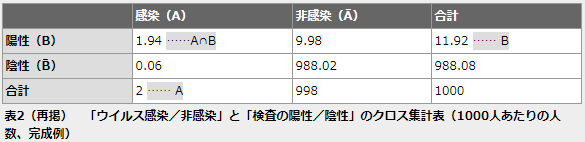
では、念のため、P(H1|D)の値も求めておきましょう。表3を再掲し、既に分かっている値も示しておきます。
| 感染(H1) | 非感染(H2) | 合計 | |
|---|---|---|---|
| 陽性(D) | 0.00194 | 0.00998 | 0.01192 |
| 陰性 | 0.00006 | 0.98802 | 0.98808 |
| 合計 | 0.002 …… P(H1) | 0.998 …… P(H2) | 1 |
| 表3(再掲) 「ウイルス感染/非感染」と「検査の陽性/陰性」のクロス集計表(数値は確率) | |||
以下の値を公式に当てはめれば求められます。
- 分子
- P(D|H1) …… 感染していることが分かっていて陽性である確率(97%なので0.97)
- P(H1) …… 感染している確率(1000人中2人なので0.002)
- 分母
- P(D|H1) …… 上に書いた通り(0.97)
- P(D|H2) …… 感染していないことが分かっていて陽性である確率(1%なので0.01)
- P(H1) …… 上に書いた通り(0.002)
- P(H2) …… 上に書いた通り(0.998)
計算してみましょう。単に値を代入して答えを求めるだけです。
となり、前に計算した結果と合っています。ここで見た例では、Hjが2つだけでしたが、ベイズの定理を展開した公式を使えば、Hjが3つ以上の場合にも計算できることが分かったと思います。
目標と解説【その6】: ベイズ更新
データが逐次得られるときに、事前確率P(Hi)を事後確率P(D)で逐次更新していくことをベイズ更新と呼びます。事前確率P(Hi)が分からない場合に、ベイズ更新によって事前確率P(Hi)を推定するのに使われます。
ベイズ更新を理解することがここでの目標です。動画も用意してあるので、計算の流れを追いかけるのがつらい方はぜひ視聴してみてください。
動画4 ベイズ更新
具体例として、予備校の大学合格率の例で考えてみましょう。A予備校では、これまでの実績からXX大学への合格率が80%(=4/5)であると分かっているものとします。一方、A予備校以外の合格率は60%(=3/5)と分かっているものとします。ちょっとわざとらしいですが、話を簡単にするために、この確率は年度によって変わらないものとしましょう。
XX大学での合格発表があり、同じ予備校のグループにいた何人かの人に順にインタビューしたところ、以下のようになりました。
- 1人目:合格
- 2人目:合格
- 3人目:不合格
このとき、このグループがA予備校の出身者のグループである確率を求めてみましょう。
なので、この式に沿って問題を整理しておきましょう。A予備校の出身者であることをHAとし、それ以外の受験生であることをHBとします。また、合格を単にDと表すことにします。不合格はD̄です(※編集部注:余事象を表す「文字のオーバーライン」は本稿のテキスト文では「Ā」「D̄」のようにDでは分離されて表示されますので、ご了承ください。適宜、読み替えてください)。
- 事後確率
- P(HA|D) …… 合格だと分かったときにA予備校の出身者である確率
- 事前確率
- P(HA) …… A予備校の出身者である確率: 取りあえず1/2
- P(HB) …… A予備校以外の出身者である確率: 取りあえず1/2
- 尤度
- P(D|HA) …… A予備校の出身者であることが分かっているとき、合格する確率: 4/5
- P(D|HB) …… A予備校の出身者以外であることが分かっているとき、合格する確率: 3/5
- P(D̄|HA) …… A予備校の出身者であることが分かっているとき、不合格となる確率: 1/5
- P(D̄|HB) …… A予備校の出身者以外であることが分かっているとき、不合格となる確率: 2/5
- 周辺尤度
- P(D|HA)P(HA)+P(D|HB)P(HB) 後で計算する
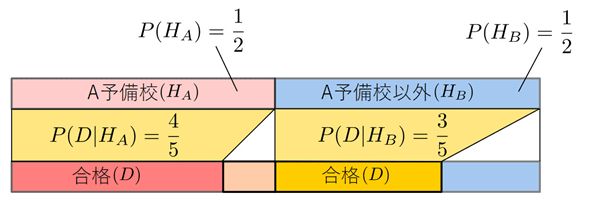
事前確率は分からないので、取りあえず1/2(=0.5)ずつにしておきました(理由不十分の原則:明確な根拠がない場合は同じ確率とします)。事後確率を求めるための値は全て出そろっています。取りあえず、必要な部分だけ図にしておくので、確認してから進めましょう。
ここからの計算は穴埋め問題にします。オレンジ色の部分をクリックまたはタップすると答えが表示されます。まず、周辺尤度だけを計算します。
4 1 3 1
= ─── ⋅ ─── + ─── ⋅ ───
5 2 5 2
4 3
= ─── + ───
10 10
7
= ───
10
事後確率P(HA|D)は以下のようになります。
4 1
─── ⋅ ───
5 2
= ───────────
7
───
10
4
───
10
= ───────
7
───
10
4 10
= ─── × ───
10 7
4
= ───
7
事後確率は4/7=0.571なので、得られた情報から、A予備校出身者のグループである確率が少し高まりました。この事後確率を次の事前確率として使います。つまり、
とします*4。
*4 A予備校以外の出身者の事後確率も同様にして求めて、次の事前確率として使うこともできますが、ここでは、事象HAと事象HBが排反なので、1−4/7で求めました。ただし、Hiが3つ以上ある場合は、1から引くというわけにはいかないので、それぞれの事後確率を同様の計算で求める必要があります。
この時点での事前確率は以下の図のように更新されています。
2人目も合格でした。同様に計算してみましょう。だいぶ慣れてきたでしょうから一気に事後確率を計算しましょう。
4 4
─── ⋅ ───
5 7
= ───────────────────
4 4 3 3
─── ⋅ ─── + ─── ⋅ ───
5 7 5 7
16
───
35
= ───────
25
───
35
16 35
= ─── × ───
35 25
16
= ───
25
計算の流れをよく見ると、分母と分子はいずれも分数で、それぞれの分母の部分は同じ値(上の例なら35)になり、約分されて消えてしまうので、実際にはその部分の計算をしなくても答えが求められます。事後確率は16/25=0.64なので、得られた情報から、A予備校出身者のグループである確率がさらに少し高まりました。この事後確率を次の事前確率として使いましょう。
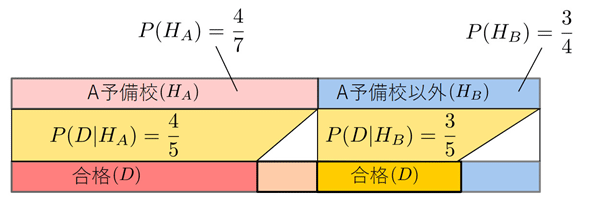
3人目は、残念ながら不合格だったということなので、尤度は以下のようになります。
- 尤度(再掲)
- P(D̄|HA) …… 1/5
- P(D̄|HB) …… 2/5
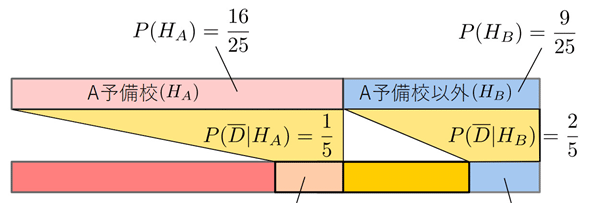
これも図で表しておきましょう。
事後確率を求めましょう。分母と分子の両方の分母部分(5⋅25の部分)は消えるので簡単に計算ができます。
1 16
─── ⋅ ───
5 25
= ───────────────────
1 16 2 9
─── ⋅ ─── + ─── ⋅ ───
5 25 5 25
1 ⋅ 16
= ─────────────
1 ⋅ 16 + 2 ⋅ 9
16
= ───
34
8
= ───
17
事後確率は8/17=0.47なので、A予備校出身者のグループである確率が減りました。……という具合に試行を逐次繰り返し、事後確率を使って事前確率を更新していくと、少しずつよりよい推定値に近づいていくというわけです。
次回は……
前回〜今回は、確率と統計のうち、主に確率について、その基礎とベイズの定理の考え方、計算方法などについて見てきました。とはいえ、取り扱った例は単純で、値も離散的なものばかりでした(離散的な値はグラフにすると棒グラフで表されるようなとびとびの値ですが、連続的な値はスムーズな曲線で表されるような値です)。次回は、離散的な値だけでなく、連続的な値も含めた分布を中心に統計の基礎を見ていくことにします。
Copyright© Digital Advantage Corp. All Rights Reserved.