中学・高校数学で学ぶ、数学×Pythonプログラミングの第一歩:数学×Pythonプログラミング入門
「Pythonの文法は分かったけど、自分では数学や数式をプログラミングコードに起こせない」という人に向けて、中学や高校で学んだ数学を題材に「数学的な考え方×Pythonプログラミング」を習得するための新連載がスタート。連載コンセプトから、前提知識、目標、本格的に始めるための準備までを説明する。
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
今回は、それに先だって、プログラミングを学ぶ上で数学を使うことのメリットや、Pythonでどのようなことができるのかを概観することにします。
1. 問題解決の方法を学ぶための最強のツールとは
プログラミングは問題解決のための強力な方法の一つです。プログラミングを学ぶことは、プログラミング言語の文法を身に付けることだけではなく、問題解決の方法を学ぶことでもあります。
では、問題解決の方法をどのようにして身に付ければいいのでしょうか。実は、私たちは中学や高校の数学(もちろん小学校の算数も含めて)で問題解決の方法を学んできています。数学とプログラミングは親和性が高いので、これまでに学んだ数学の知識を少しずつ思い出しながらプログラミングを学ぶのは効果的な攻め方です。また、AI/機械学習などの手法は数学を使って構築されているので、数学的な考え方を身に付けることは、これからのプログラマーにとっては必須のスキルといっていいでしょう。
とはいえ、数学に苦手意識を持つ人も少なからずいると思います。が、この連載では基本的な考え方を理解することに重点を置いてお話を進めるので、安心して読み進めてください。目標はズバリ、数式を見れば自分でプログラミングできるようになることと、AI/機械学習などで使われている数式を理解するための基礎力を身に付けることです。この2点について「2. 文法からアルゴリズムへ」と「3. 数学×Pythonを学ぶことの相乗作用」で説明します。
2. 文法からアルゴリズムへ
プログラミングに挫折した人の多くは「文法は分かるんだけど、自分でプログラムを作ろうと思うと途方に暮れてしまう」と口をそろえて言います。そのことについて、簡単なプログラムを例に考えてみましょう。
以下のプログラムは、フィボナッチ数列の先頭からn個分のリストを作るプログラム(関数makefib)の作成例です。今はまだコードの意味を詳しく説明しないので、分からなくても全く問題ありません。ざっと雰囲気だけ眺めてください。なお、この連載では開発環境としてGoogle Colaboratoryのscratchpadを使います。そこで、プログラムの作成手順を簡単に説明するための動画を用意しておきました。プログラムの中身については触れませんが、どういう手順でプログラムを作り、実行するかが分かるようになっているので、はじめての方はその流れをぜひ動画で確認しておいてください。
動画1 Google Colabでプログラム作成から実行まで
def makefib(n): # 関数の定義
fib = []
for i in range(0,n):
if i == 0 or i == 1:
fib.append(i)
else:
fib.append(fib[i-2]+fib[i-1])
return fib
makefib(10) # 関数を呼び出して先頭から10項分を表示する
# 出力例:[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
*1 Pythonのプログラムではインデント(字下げ)が、関数定義や繰り返し処理などの範囲を表すのに重要な意味を持ちます。Pythonの書き方についてのガイド(PEP8と呼ばれます)では、4つの半角スペースを使うことが推奨されていますが、この連載では、Google Colaboratoryの標準設定に合わせて2つの半角スペースにしてあります。
関数の定義はたったの8行ですが、Pythonのプログラムでよく使われる初歩的なキーワードや記号が登場しています。順に抜き出して見ると以下のようになります。
- キーワード def for in if or else return
- 記号など () : [] = == + -
- 識別子など makefib n fib i range append
これらのキーワードや記号の意味を理解するのはそう難しいことではありません。また、どのようなプログラムであっても、基本的には以下の処理を組み合わせれば作成できることも想像に難くありません(上のプログラムにもこれらの処理が全て含まれています)。
- 順次処理: 文を上から順に実行していく
- 選択処理: いずれかの文を実行する(いわゆる条件分岐)
- 反復処理: 文を何度も実行する(いわゆる繰り返し処理)
しかし、実際にプログラムを作ろうとすると、どこから手を付けていいのか分からないというわけです。
では、いったい何が足りないのでしょうか。それは、問題をどのように表現し、処理の組み合わせに落とし込んでいくかというスキルです。それができれば、Pythonの文法に従ってプログラムを書くことはさほど難しいことではありません。
- 問題を適切な形で表現する
- 処理の組み合わせに落とし込む
- Pythonの文法に従って書く ← ここは比較的容易
アルゴリズムは計算の手順のことですが、上の1と2を考えることにほかなりません。そして、私たちは数学を通してこれまでにかなりのことを学んできています。忘れてしまったものもあるかもしれませんが、公式や解法のパターンを見ればすぐに思い出せるはずです。私たちは、すでに問題解決のための「引き出し」をたくさん持っているのです。それらをプログラミングの学習に使わない手はありません。そういうわけで、この連載では、中学・高校の数学を思い出しながら、それらを使って特に数学に関するPythonのプログラミングを効率良く学ぼうというわけです。
なお、フィボナッチの数列のプログラムは、数学での定義そのままです。数列の先頭の項を第0項とし、各項をnと表すなら、以下のようになります。
- i=0のときn0=0
- i=1のときn1=1
- i>1のときni=ni−2+ni−1 ⋯
[A]
最後の[A]を「ある項の値は、2つ前の項と1つ前の項を足したもの」と日本語に翻訳できれば、あとはPythonの文法に従って、順に数列のリストを作っていくだけです。
コラム 良いアルゴリズムと数学の知識
フィボナッチの数列を求める方法(アルゴリズム)にはさまざまなものがあります。下手な方法を使うと、計算量が指数関数的に大きくなり、nが増えるととてつもなく時間がかかってしまい、実用に耐えなくなります。しかし、アルゴリズムを改善したり、数学的な知識を使って式を変形したりすることにより、計算量を減らすことができます(ちなみにリスト1の計算時間はnに比例します)。そのことについては回を改めて紹介しようと思いますが、実は、フィボナッチの数列の第n項anを求めるには、以下の式が使えます。
つまり、第n項だけを求めるなら、0から順に計算していかなくても、この式を当てはめるだけで求められるというわけです。数学的な知識といっても、それほど高度な知識が必要になるわけではないので、より効率のいい方法や、より簡単に計算できる式についての知識も少しずつ増やしていくと、問題解決の大きな力になります。また、単純な足し算の繰り返しなのに、なぜか√5が登場するなど、数学の不思議さも楽しめます。
3. 数学×Pythonを学ぶことの相乗作用
前項でも述べたように、数学で培った問題解決のスキルはプログラミングに活用できます。一方、プログラミングは、一つ一つの単純な手順を組み合わせながら複雑な処理を組み立てていく作業です。したがって、それらの手順を丁寧に追いかけていく中で、数学の公式や解法を使った計算がどのように行われていくのかを具体的に確認できます。そのことにより、逆に数学の理解を深めることもできます。数学とプログラミングの学びには相乗作用があるというわけです。
以下のプログラムは、ベクトルの内積を求めるプログラムですが、プログラムの動きを追いかけることにより、内積の計算方法もしっかり理解できるようになります(これについても、今はコードの意味が分からなくても全く問題はありません)。
def inner_product(x,y): # 関数の定義
sum = 0
for i in range(0,len(x)): # xとyは同じ次元であるものとする
sum += x[i]*y[i]
return sum
inner_product([2,3],[4,5]) # 関数を呼び出して[2,3]と[4,5]の内積を求める
# 出力例:23
ベクトルx=(x1,x2,...,xn)とベクトルy=(y1,y2,...,yn)の内積は以下の式に従って計算します。xとyの対応する要素の積の総和なのですが、この式だけを見てもイメージが湧かなかった人もいるかもしれません。
プログラムを見ると、総和を求めるΣの働きが具体的な手順として表されているので、静的に見えた数式が動的に見えてくるようになります。中学・高校で十分理解できていなかった数式や大学レベルの数式についての理解が助けられるというわけです*2。
*2 数学を通してPythonプログラミングを学ぶことは、いわば「一石二鳥」の効果を持ちます。が、逆に「二兎を追う者は一兎をも得ず」にならないように、なじみの薄い公式や定理については、できるだけやさしく丁寧に解説することにします。
なお、内積の計算は、AI/機械学習の多くの手法で使われる基本的な計算です。「応用」は基本的な事柄の組み合わせなので、基本の理解を深めておけば、スムーズな応用にもつながります。
4. 前提知識と目標
これまでにお話ししたように、この連載では中学・高校で学ぶ数学を使って、プログラミングを学びます。サンプルプログラムとしては主に数学に関するものを取り上げますが、前提知識として中学・高校の数学をマスターしている必要は全くありません。教科書に掲載されていた公式ならなんとなく覚えがあるといったレベルで十分です。試験でさんざん苦しめられたトラウマのせいで、苦手意識を持つようになったという人も(実は、筆者もその一人です)安心して読み進められるようにするつもりです。
数学に関しては、事前に参考書などを読んでおかなくても理解できるように説明しますが、それでも不安があるという方は、『AI・機械学習の数学入門 ― 中学・高校数学のキホンから学べる』の「中学/高校数学のおさらい 〜 微分/線形代数につながる基礎」の部分に目を通していただくといいでしょう。
Pythonのプログラミングに関しても、なんとなく文法を覚えているといったレベルで十分です。必要に応じて文法についてのまとめを入れるので安心して取り組んでください。多少の不安があるという方は、『Python入門』を参照していただくといいでしょう。
この連載のゴールは、最初にもお話しした通り、AI/機械学習で使われている数式を理解するための基礎力を身に付けることと、数式を見れば自分でプログラミングができるようになることです。連載の流れによっては順序や内容が変わることもあるかもしれませんが、次回からは図2に示すようなテーマごとに例を取り上げ、サンプルプログラムを作りながら、ゴールに一歩ずつ近づいていきたいと思います。
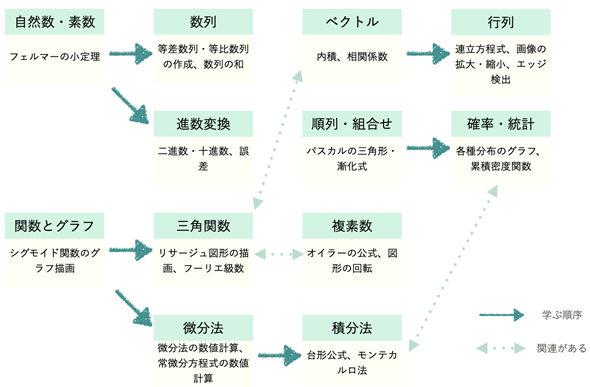
図2 本連載のゴールと学べる内容
各テーマの下に取り扱う例を示してある。学ぶ順序に決まりはないが、比較的自然な流れが分かるようにした。また、どのテーマも互いに関連しているが、特に関係があるものを点線の矢印で示した。
5. Pythonプログラミングの準備と便利なライブラリ
次回以降の記事では、サンプルプログラムと解説を読み進めるだけでも知識は得られますが、やはり、実際にプログラムを作りながら読み進めた方が確実に身に付きます。そこで必要となるのがPythonの開発環境です。取りあえずサンプルプログラムを試してみたいという方には、Google Colaboratory(以下、Colab)のscratchpadをおすすめします。以下のサイトにアクセスすると、ブラウザ上でPythonのプログラミングができるようになります。上で述べたように、この連載ではGoogle Colabのscratchpadの画面で説明します。
ただし、Googleのアカウントでログインする必要があります。
本格的にPythonのプログラミングに取り組みたい方は、Anaconda開発環境個人版を以下のサイトからインストールして利用するといいでしょう。
Ancondaを起動し、Jupyter NotebookまたはJupyterLabを選択すると、ブラウザが起動し、プログラムのコードを入力できるようになります。
いずれの環境でも、コードを入力した後、[Shift]+[Enter]キー(Windowsの場合。Macなら[shift]+[return]キー)を押せば、すぐに実行できます。
Google ColabもAnaconda開発環境個人版も無償で使えます。また、さまざまなライブラリ(目的ごとに、便利なプログラム部品をひとまとめにしたもの)が数多く提供されているので、高度な機能も簡単に呼び出して使えます。表1に示すのはこの連載で使う主なライブラリとよく使われる機能(関数)の一覧です。
| ライブラリ名 | 用途 | よく使う関数 |
|---|---|---|
| 組み込み関数 | プログラムで一般的に使われる関数 (特に何も指定しなくても使える) |
abs, format, id, input, int, len, list, max, min, print,range, round, sorted, sum, tuple |
| math | 数学のための関数 | ceil, comb, cos, degrees, dist,exp, factorial, floor, gamma, gcd, lcm, log, pi, radians, sin, sqrt, tan, trunc |
| random | 乱数作成のための関数 | betavariate, expovariate, normalvariate, random, randrange, seed, shuffle, uniform |
| numpy | 科学技術計算のための関数 | arange, array, copy, diagonal, mean, ones, reshape, shape, sum, transpose, zeros |
| matplotlib.pyplot | グラフ描画のための関数 | axes, hist, imshow, pie, plot, scatter, show, xlabel, ylabel |
これらは、Pythonから利用できるライブラリのあくまでごくごく一部です。この他にも圧倒されるほど数多くのライブラリとそれらで利用できる関数などの機能が提供されているので、興味のある方はPython公式ドキュメントの「Python標準ライブラリ」(https://docs.python.org/ja/3/library/index.html)をざっと眺めてみてください。
さて、今回は中学・高校の数学を使ってPythonのプログラミングを学ぶことのメリットや前提知識、目標などについてお話をし、最後に開発環境の利用方法を紹介しました。
次回からは、いよいよ具体的な例を使ってプログラミングに取り組んでいきたいと思います。次回は、フェルマーの小定理と呼ばれる簡単な定理(中学の数学で理解できる内容です)のプログラミングを通して、計算の方法、変数、関数の作り方などについて学びます。
動画2 中学・高校数学で学ぶ、数学×Pythonプログラミング
Copyright© Digital Advantage Corp. All Rights Reserved.