Matplotlibで折れ線グラフ（正規分布など）を描こう：数学×Pythonプログラミング入門（3/3 ページ）

「モデルとデータの可視化」というテーマで関数グラフの描画やヒストグラムや散布図などの各種グラフの取り扱い方を前後編で解説。前編である今回はシグモイド関数のグラフを描く問題を手始めに、さまざまなグラフの描画方法を見ていく。

[羽山博，著]

練習問題

　練習問題でどのようなものを作成すればいいかが分かるように、実行例を動画で紹介しています。ぜひ視聴してみてください（解答例のコードについては解説に従ってひたすら入力するだけになるので、動画では1行ずつ細かく説明することはしていません）。

動画2　練習問題の実行例〜フーリエ級数による矩形波の描画、3D散布図、回帰直線の表示

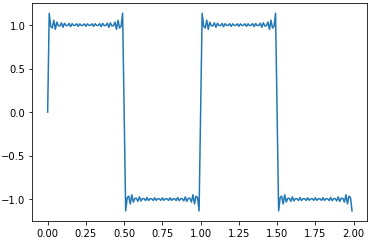
（1）フーリエ級数を利用して矩形波を描画する

　矩形波（くけいは）とは、下の実行例に見られるような矩形（くけい：四角い形）の波で、フーリエ級数によって表すことができます。フーリエ級数とは、さまざまな関数を三角関数の無限級数（無限に足していくこと）で表したものです。矩形波の場合は以下のような式になります。

　では、x＝0〜2の範囲（2秒間）を0.01ずつで刻んだグラフを描いてみてください。周波数（1秒当たりの波の数）を表すfは1とします。また、上の式ではΣの上限は∞ですが、無限に繰り返すことはできないので、繰り返しの最大数を20回としましょう。

　実行例は図7のようになります。

図7　フーリエ級数を使って矩形波を描いた例
この例では、時間を2、周波数fを1として描いているので、周期1/f＝1の波が2つ表示される。繰り返しの最大数を増やすとスムーズなグラフになる。

（ヒント）　まず、x, f, kmaxの値を指定して、yの値を求める関数fourierを作成しましょう。これは、数式をそのまま関数にすればいいだけですが、総和（Σ）を計算するので、繰り返し処理を使う必要があります（総和の計算は前回やりましたね）。次に、xの値を最小値（0）から最大値（2）まで、0.01刻みで変えながら、yの値を求め、xのリストとyのリストを作ります。これはリスト14で作成した関数makedataを呼び出すだけでできます。というわけで、以下に示すリスト17のfourier関数が作成できればグラフが描けます。

import numpy as np
import matplotlib.pyplot as plt

def fourier(x, f, kmax):
  # この中身を書いてください

args = {'f': 1, 'kmax': 20} # 周波数と繰り返し数を指定する
x, y = makedata(fourier, 0, 2, 0.01, **args) # リスト14の関数を呼び出す
plt.plot(x, y)

リスト17　矩形波を描画するためのコード（未完成）
関数makedataはリスト14で作ったもの。引数にはデータを作るために使う関数名（ここではfourier）、xの定義域の最小値（0）、xの定義域の最大値（2）、増分値0.01、データを作るために使う関数（fourier）に渡す可変個の引数**argsを指定する。

（2）多変数関数で表された曲面のグラフを描く

　曲面を描画する例は、本編では紹介していませんが、numpyモジュールのmeshgrid関数を使って座標の配列を作成し、matplotlib.pyplotモジュールのplot_surfaceメソッドの引数に指定すれば、簡単に曲面が作成できます。その部分のコードについては、あらかじめ書いておきます。今回学んだ内容に関係するのは、数式に従ってデータを作成する部分です。その部分を書いてみてください。

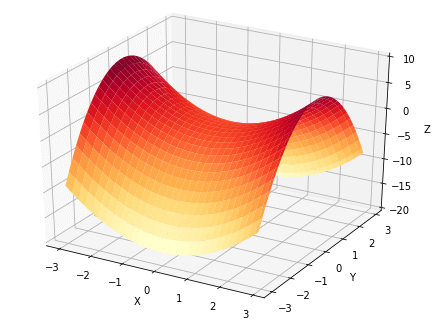
　ここでは、「［AI・機械学習の数学］偏微分の基本（意味と計算方法）を理解する」で、多変数関数の例として紹介した以下の式をグラフ化してみます。

　ただし、−3 ≤ x < 3、−3 ≤ y < 3の範囲で、x, yともに0.1刻みでグラフを描くことにします。

　リスト18のコードを穴埋めして完成させてください。正しく実行できれば、曲面のグラフが描けます。

import numpy as np
import matplotlib.pyplot as plt 

x = np.arange(___ア___) # -3以上3未満まで0.1刻みで
y = np.arange(___イ___) # -3以上3未満まで0.1刻みで
x, y = np.meshgrid(x, y) # 座標の配列を作る
z = ___ウ___  # 多変数関数の式をPythonのコードとして書く

plt.figure(figsize=[8, 6])
ax = plt.subplot(projection='3d')
ax.set_zlim(-20, 10) # zの範囲は-20〜10までとする
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.plot_surface(x, y, z, cmap='YlOrRd') # カラーマップは黄色から赤
plt.show()

リスト18　曲面を描画するためのコード（未完成）
meshgrid関数は、xとyで指定された範囲の全ての座標の配列を返す（後述）。それを使ってzの値を求めるとデータの準備ができる。あとはplot_surfaceメソッドにx,y,zを指定するだけ。ここでは、色が黄色からオレンジを経て赤に変わるように、カラーマップとして'YlOrRd'を指定した（YellowOrangeRedの略）。

　実行例は図8の通りです。

図8　多変数関数z＝x²−2y²で表される曲面を描いた例
xの値は-3〜3まで0.1ずつ変わり、yの値も-3〜3まで0.1ずつ変わる。その全ての座標の組み合わせに対するzの値を求め、曲面を描く。

（ヒント）　ここでは、meshgrid関数の働きを知らなくても、解答はできますが、やはり、分かっていた方が見通しがよくなります。簡単な例で見てみましょう。例えば、x=[1,2,3],y=[4,5,6]とすると、meshgrid関数はそれらの交点に当たる全ての座標の配列を返します（リスト19、図9）。

import numpy as np

x = [1, 2, 3]
y = [4, 5, 6]
np.meshgrid(x, y)
# 出力例：
# [array([[1, 2, 3],
#         [1, 2, 3],
#         [1, 2, 3]]), # x座標に当たる要素
#  array([[4, 4, 4],
#         [5, 5, 5],
#         [6, 6, 6]])]  # y座標に当たる要素

リスト19　meshgrid関数の働き
これについては以下の図9で一目瞭然なので、そちらを参照するとよい。

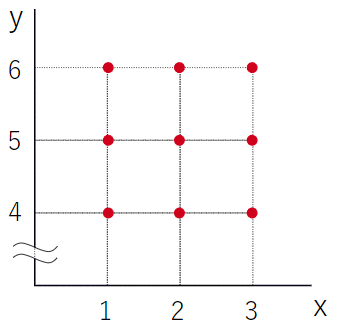
図9　meshgrid関数により作成される座標配列
リスト19に示したmeshgrid関数の出力例は上の9つの点の座標を表している。出力例のx座標に当たる要素とy座標の当たる要素を先頭から対応させて順に並べてみると、9つの点の座標(1, 4), (2, 4) ,(3, 4), (1, 5), (2, 5) ,(3, 5), (1, 6), (2, 6), (3,6)になっていることが分かる。

練習問題の解答例

　以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではありません。

（1）フーリエ級数を利用して矩形波を描画する例

　一見、難しそうですが、数式をそのまま関数として表現するだけです。これまで、繰り返し処理を使わずに配列の要素を計算する方法を見てきましたが、総和を求めるためには繰り返し処理が必要になります。

import numpy as np
import matplotlib.pyplot as plt

def fourier(x, f, kmax):
  tmp = 0
  for k in range(kmax):
    tmp += np.sin(2*(1+2*k)*np.pi*f*x) / (1+2*k)
  return tmp * 4 / np.pi

args = {'f': 1, 'kmax': 20}
x, y = makedata(fourier, 0, 2, 0.01, **args)
plt.plot(x, y)

リスト20　矩形波を描くためのコード（完成例）
関数fourierのtmp=0からreturn文の前までの3行は、リスト内包表記を使って、tmp = sum([np.sin(2*(1+2*k)*np.pi*f*x) / (1+2*k) for k in range(kmax)])と書くこともできる。sum関数はリストの要素の総合計を求める組み込み関数。

（2）多変数関数で表された曲面のグラフを描く

　meshgrid関数やplot_surfaceメソッドについては、取りあえずそのまま書けばいいですね。問題はarange関数を使って連続値を作るところと、関数を表す数式をPythonのコードで書くところだけなので、難なくできると思います。答えは以下の通りです。

（答え）
ア. -3, 3, 0.1
イ. -3, 3, 0.1
ウ. x**2 - 2*y**2

---

　今回は、ビジュアライズ（可視化）というテーマの前半として、関数のグラフを描く方法を見ました。NumPyの機能を使って、プロットするためのデータを作成する方法についてのお話が多くなりましたが、可視化によって、モデルが理解しやすくなったり、データの分布や変数同士の関係などについてのイメージを得たりするのに役立つことが分かったかと思います。

　次回（後編）では、関数で表されるグラフではなく、収集したデータや分析結果を棒グラフやヒストグラム、散布図などで表し、データの特徴を可視化する方法を見ていきます。今回作成したグラフは、いわば理論的なモデルを可視化したものですが、次回は、現実の値を分析するためにデータを可視化する、というわけです。

「数学×Pythonプログラミング入門」