Pythonでグラフを描こう ― 棒グラフ/ヒストグラム/散布図/ヒートマップ:数学×Pythonプログラミング入門(1/3 ページ)
「モデルとデータの可視化」というテーマで各種グラフの描画方法を前後編で解説。後編である今回は、棒グラフ/ヒストグラム/箱ひげ図/散布図/ヒートマップを作成し、複数のグラフを並べて表示する方法を説明する。
前回は、「ビジュアライズ(可視化、視覚化)」というテーマの前編として、関数をグラフ化することによりモデルを可視化する方法を見ました。今回は後編です。収集したデータや分析結果を可視化するために、棒グラフやヒストグラム、散布図、ヒートマップなどを作成します。
今回の練習問題としては、3D散布図と個別の2D散布図を並べて描く例、回帰分析を行って散布図に回帰直線を重ねて描く例を取り上げます。もちろん、全て中学/高校までの数学の知識があれば作成できるプログラムです。グラフ化するデータの準備についてはある程度Pythonの経験がないと難しい部分もありますが、分からない部分については「おまじない」だと思ってサンプルコードをそのまま入力してもらって構いません。
見出し/図/リスト/脚注などの番号は、前編である前回からの続き番号となっています。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。
目標3: さまざまなグラフを描画する
前回は、折れ線グラフを使って関数のグラフを描く方法を見てきましたが、実用面を考えると、数式をグラフ化する方法だけでなく、収集したデータや分析結果をグラフ化する方法についても身に付けておきたいところです。目的に合わせてさまざまな種類のグラフを作成したいですね。
そこで、これだけ知っていればあとは自力で調べながら必要なグラフが描ける、というレベルに到達できる基本的な事例を幾つか紹介することにします。以下のようなグラフが作成できることを目指しましょう。
- [1]棒グラフの作成(単一の系列、複数の系列) …… 数値の規模を見る/比較する
- [2]ヒストグラムの作成 …… 分布を見る
- [3]箱ひげ図の作成 …… 分布や外れ値を見る
- [4]散布図の作成 …… 変数同士の関係を見る
- [5]ヒートマップの作成 …… クラスタの人数などを可視化する
また、複数のグラフを使った比較を行うために、以下の方法についても紹介します。
- [6]複数のグラフを並べて表示する
以下、数学的に難しい概念や計算は出てきませんが、pandasモジュールを使って分析のためのデータを作成する方法やmatplotlib.pyplotモジュールのさまざまなグラフ作成機能など、より実用的な機能の利用について見ていきます。今回は小さなサンプルプログラムばかりなので、作成から実行までの大きな流れが把握しづらいことはないと思います。というわけで[1]〜[5]までの動画は用意していません([6]以降の動画は用意されているので、後ほどご覧ください)。
6. さまざまなグラフを描画する(プログラムの作成)
[1]棒グラフの作成
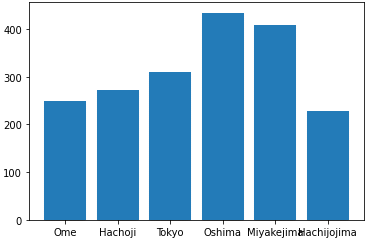
棒グラフは、数値の規模を見たり、数値を比較したりするのに役立ちます。棒グラフの作成には、matplotlib.pyplotモジュールのbar関数を使います。横軸のラベルとグラフ化するデータを用意しておけばグラフが描けます。以下の例は、東京都の幾つかの地点での2021年7月の月間降水量をグラフにしたものです(出典:気象庁の「過去の気象データ」)。
import matplotlib.pyplot as plt
location = ['Ome', 'Hachoji', 'Tokyo', 'Oshima', 'Miyakejima', 'Hachijojima']
amount = [248.5, 273.0, 310.0, 434.5, 408.5, 229.0]
plt.bar(location, amount)
locationが横軸のラベル、amountがグラフ化する値。このままだと、横軸のラベルが少し重なるので、気になるようであれば、bar関数の前にplt.figure(figsize=[7, 4])などと入力してグラフのサイズを変えるとよい。
リスト21の実行例は図10の通りです。
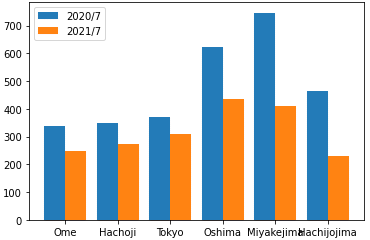
複数の系列を描画するなら、最初の系列の幅(引数width)に負の値(例:-0.4)を指定し、2番目の系列の幅に正の値(例:0.4)を指定します。負の値を指定すると、横軸のラベルの左側に向かって棒の幅が広がり、正の値を指定すると、横軸のラベルの右側に向かって棒の幅が広がります。あとは、位置(引数align)を横軸の端(edge)に合わせるようにすれば2つの系列が並びます。2020年7月の月間降水量と2021年7月の月間降水量を比較してみましょう(出典:気象庁の「過去の気象データ」)。
import matplotlib.pyplot as plt
location = ['Ome', 'Hachoji', 'Tokyo', 'Oshima', 'Miyakejima', 'Hachijojima']
amount202007 = [337.5, 350.0, 370.0, 623.5, 746.5, 462.5]
amount202107 = [248.5, 273.0, 310.0, 434.5, 408.5, 229.0]
plt.bar(location, amount202007, width=-0.4, align='edge', label='2020/7')
plt.bar(location, amount202107, width=0.4, align='edge', label='2021/7')
plt.legend(loc=2)
最初の系列ではwidth=-4を指定しているので、横軸のラベルの左側に向かって棒の幅が広がる。次の系列ではwidth=4を指定しているので、横軸のラベルの右側に向かって棒の幅が広がる。align='edge'とし、棒の位置を横軸の端に合わせると2つの系列が並ぶようになる。なお、labelに文字列を指定しておき、legend関数を呼び出すと系列の色とlabelの文字列が凡例として表示される。凡例の位置は引数locで指定する。1なら右上、2なら左上、3なら左下、4なら右下などとなる。
実行例は図11の通りです。
複数の系列を並べるための設定については、図12の図解を見ると分かりやすいと思います。

図12 複数の系列を並べるための設定
align='edge'は、目盛りに棒の左端を合わせるという設定。棒はwidthで指定された幅で描画される。widthに負の値を指定すると左右が反転するので、棒の右側が目盛りに合った形になる。
[2]ヒストグラムの作成
ヒストグラムは棒グラフに似ていますが、度数分布表を基に頻度(ひんど:値の個数)を棒グラフにし、分布を可視化したものです。普通、棒と棒の間にスペースは設けません。といっても、いちいち度数分布表を作ってから、頻度を棒グラフにし、棒と棒の間にスペースが入らないように調整するという必要はありません。もちろん、そのようにしても作れますが、hist関数を使えば元のデータから直接ヒストグラムが作成できます。
以下の例は、架空の成績データ(ですが、某大学の授業での傾向に合わせて作ったものです)を基にヒストグラムを作成したものです。
データ数がある程度多くないとヒストグラムを描いてもつまらないので、GitHubに置いてあるCSVファイル(値をカンマで区切って表したテキストファイル)のデータを利用することにしました。ここでは、データ分析のために使われるpandasモジュールのread_csv関数を使ってCSVファイルを読み込むことにします。read_csv関数では、ファイルだけでなく、WebサイトからCSVファイルを取得することもできます。返されるデータはpandasのデータフレーム(DataFrame)と呼ばれる表形式のデータなので、直感的にも分かりやすく、扱いやすいと思います。以下の例では、データの形式と内容が分かるように、headメソッド*8を使って最初の5行だけ表示してあります。
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Gessys/math/main/data/score.csv')
df.head()
read_csv関数の引数に、ファイルのURLやパス名を指定するだけで、CSVファイルのデータが取得され、データフレームとして返される。引数の指定により、データの取り扱いについての詳細な設定もできるが、ここでは省略する(気になる方は「pandas公式APIドキュメント」を参照されたい)。headメソッドは先頭から何行かを返す関数。引数を指定しないと5が指定されたものと見なされる。
*8 メソッドは日本語にすると「方法」といった意味ですが、クラスに含まれる関数のことで、一般的な関数とは区別されます。Pythonでは例えば、モジュール名.hogehoge()なら「関数」、クラスインスタンス名.hogehoge()なら「メソッド」と呼ばれます。ただし、hogehoge()という記載だけの場合など、「メソッドなのか、関数なのか」の見分けが付かないこともあります。見分けが付かなくても実用上の問題は基本的にありませんが、メソッドか関数かを見分けたい場合は、print(hogehoge)のようなコードで関数名/メソッド名を指定してその情報を出力すると、関数の場合は「<function ……>」のように、メソッドの場合は「<bound method ……>」のように表示されるので、どちらかを判別できます。
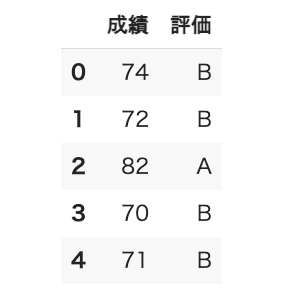
実行例は図13のようになります。CSVファイルには数値も全て文字列として入力されていますが、数値として解釈できる場合は、自動的に数値に変換されます(ここでは成績の値は整数int64に変換されます)。
では、ヒストグラムを作成してみましょう。列のデータはデータフレームに['列名']を指定すると取り出せます。返されるデータはpandasのSeriesと呼ばれる形式ですが、そのままhist関数に指定できます。Seriesは日本語に訳しにくいのでそのまま「シリーズ」と呼ばれますが「一連」や「連続」といった意味です。「系列」と訳されることもあります。
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Gessys/math/main/data/score.csv')
scores = df['成績'] # 「成績」列データを取得
plt.hist(scores, bins=8, range=[20, 100])
binsには階級(区間)の数を指定してもいいし、各階級の最小値をリストとして指定してもいい。rangeにはグラフ化の対象となる値の最小値と最大値が指定できる。この例であれば20以上100未満がグラフ化される(13点の人が1人いるがヒストグラムには表示されない)。ただし、実際には最後の階級に100という値が含まれたヒストグラムが表示される。詳細はこちらの公式APIドキュメントを参照。
実行例は図14の通りです。
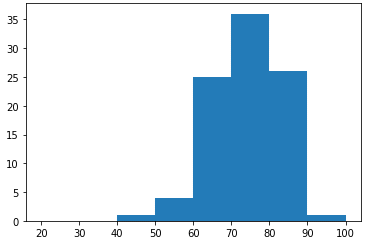
図14 成績をヒストグラムにしたもの
横軸の目盛りから次の目盛りまでの間が1つの階級となる。目盛りの意味は「以上/未満」なので、例えば「30と40」の間は「30以上40未満」の階級を表す。ただし、最後の階級だけは「90以上100以下」となる。分布が視覚的に確認でき、70点以上80点未満の人が多いことが分かる。
コラム pandasでもグラフが作成できる
上の例では、matplotlib.pyplotモジュールのhist関数を使ってヒストグラムを作成しましたが、pandasデータフレームのhistメソッドを使ってヒストグラムを作成することもできます。同様に折れ線グラフ(plot)、棒グラフ(plot.bar)、散布図(plot.scatter)なども描けます。ただし、この記事ではmatplotlib.pyplotモジュールの機能を使ってグラフを描画することにします。
import matplotlib.pyplot as plt # なくても動くが、plt.show()のために書いた
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Gessys/math/main/data/score.csv')
df.hist(column='成績', bins=8, range=[20, 100])
plt.show()
histメソッドの引数にcolumn='列名'を指定すると、その列の値がヒストグラムとして表示される。binsやrangeの指定は既に見た例と同じ。
実行例は図15の通りです。
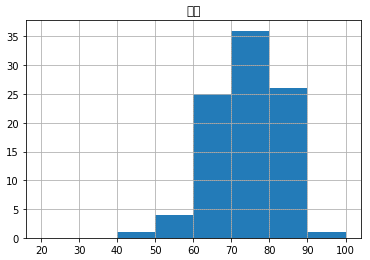
図15 pandasのDaraFrame.histメソッドでもグラフが作成できる
グリッドは自動的に表示される。histメソッドにgrid=Falseを指定すれば、グリッドが表示されないので、図14と同じ表示になる。
この例では、「成績」という列の見出しが日本語文字なので、フォントが正しく表示できないという警告メッセージが表示されます。これはmatplotlib.pyplotでplt.title('成績')と指定し、グラフのタイトルを指定した場合も同じです。グラフの上に「成績」と表示されず、文字化けしているのはそのためです(適切な日本語フォントを指定することで文字化けを回避できますが、Colabで回避するには「こちらの記事」を参考にしてみてください)。
[3]箱ひげ図を作成する
箱ひげ図は、四分位範囲(全体の順位の1/4〜3/4に当たる範囲)を「箱」で表し、四分位範囲から一定の値だけ離れた位置を「ひげ」で表して全体の分布を可視化したものです。さらに、ひげの外側にある外れ値も表示されます。後の実行例を見るとそれぞれどのように表示されるかが分かります。ちなみに、2017年に告示され、2021年から全面実施に移された学習指導要領では、統計的な考え方がますます重要になることが反映され、四分位範囲と箱ひげ図が中学の数学で取り扱うテーマになりました。
リスト26の例は、英語(english)と数学(mathmatics)の成績(架空のデータ)を基に箱ひげ図を作ったものです。箱ひげ図を作成するには、matplotlib.pyplotモジュールのboxplot関数に値のリストを指定します。
import matplotlib.pyplot as plt
english = [98, 77, 64, 45, 58, 62, 89, 30]
mathmatics = [88, 54, 72, 85, 70, 81, 63, 27]
plt.boxplot([english, mathmatics],labels=['english', 'mathmatics'])
plt.show()
複数の箱ひげ図を並べたいので、[english, mathmatics] のようにリストとして指定した(二次元のリストになっている)。箱ひげ図にするデータが1つだけならリストにしなくてもよい(例えば、英語だけの箱ひげ図を作るなら、最初の引数には単にenglishとだけ指定すればよい)。
実行例は図16の通りです。
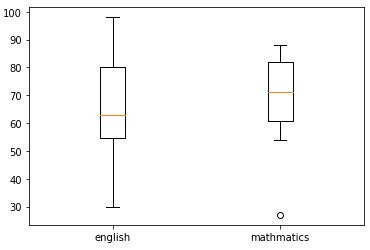
図16 英語と数学の成績を箱ひげ図にしたもの
オレンジ色の線が中央値の位置、箱は第1四分位数(Q1:下から1/4の順位の位置)と第3四分位数(Q3:下から3/4の順位の位置)まで描かれる。上下の端に表示される短い横線までが「ひげ」。ひげの端の線がどの値の位置に描かれるかは後ほど説明する。ひげの外側に値がある場合には、外れ値として○で表示される。この例であれば、数学(mathmatics)の成績の下位に外れ値があることが分かる。
箱ひげ図の基となる四分位数についても求めておきましょう。リスト27の例では、英語の成績についての要約統計量を求めています。数学の成績については、この例を参考にして、練習問題として取り組んでいただくといいでしょう。
import pandas as pd
english = [98, 77, 64, 45, 58, 62, 89, 30]
mathmatics = [88, 54, 72, 85, 70, 81, 63, 27]
sr_e = pd.Series(english) # リストをpandasのSeriesに変換
print(sr_e.describe()) # describeメソッドを使って要約統計量を求める
# 数学の要約統計量を求めるためのコードは、ここに書くとよい
#出力例:
count 8.00000
mean 65.37500
std 22.33471
min 30.00000
25% 54.75000
50% 63.00000
75% 80.00000
max 98.00000
dtype: float64
describeメソッドを使うとデータ数(count)、平均(mean)、標準偏差(std)、最小値(min)、第1四分位(25%)、中央値=第2四分位数(50%)数、第2四分位数(75%)、最大値(max)の要約統計量が求められる。数学の成績についても、同様にして要約統計量を求めておくとよい。
(答え) 数学の要約統計量をsr_mとすると以下のようになります。
sr_m = pd.Series(mathmatics)
print(sr_m.describe())
出力例のうち、箱やひげを描くのに使われる値として、以下の値が求められています。
- 第1四分位数(Q1): 25%の位置、つまり54.75
- 第3四分位数(Q3): 75%の位置、つまり80.0
図16を見ると、第1四分位数(以下「Q1」と略します)から第3四分位数(以下「Q3」と略します)の範囲に箱が描かれていることが確認できますね。この範囲を四分位範囲と呼びます。ここでは、四分位範囲はQ3−Q1=80.0−54.75=25.25です。
ひげの端の位置については、ちょっとした計算が必要です。以下、標準の設定での計算方法を示しておきます。
- 下ひげの端の位置: Q1−(Q3−Q1)×1.5以上の、最も近い値
ここでの例では、54.75−(80.0−54.75)×1.5=16.875なので、この値「以上」で最も近い30点の位置 - 上ひげの端の位置: Q3+(Q3−Q1)×1.5以下の、最も近い値
ここでの例では、80.0+(80.0−54.75)×1.5=178.875なので、この値「以下」で最も近い98点の位置
英語の場合、ひげの外側に値が存在しないので、外れ値と見なせる値は存在しません。
数学の成績についても、コードを入力してそれぞれの値を求め、同様に計算してみてください。以下のオレンジ色の部分をクリックすると、答えが表示されます。
- 第1四分位数(Q1): 60.75
- 第3四分位数(Q3): 82.0
- 四分位範囲: Q3−Q1= 21.25
- 下ひげの端の位置: Q1−(Q3−Q1)×1.5= 28.875 以上の、最も近い値(54点)
- 上ひげの端の位置: Q3+(Q3−Q1)×1.5= 113.875 以下の、最も近い値(88点)
27点という外れ値の存在も分かります。
Copyright© Digital Advantage Corp. All Rights Reserved.