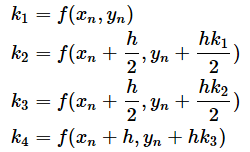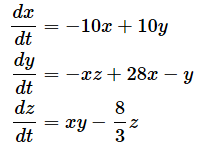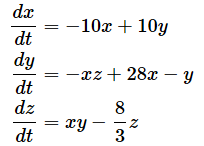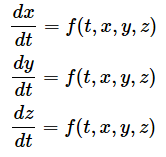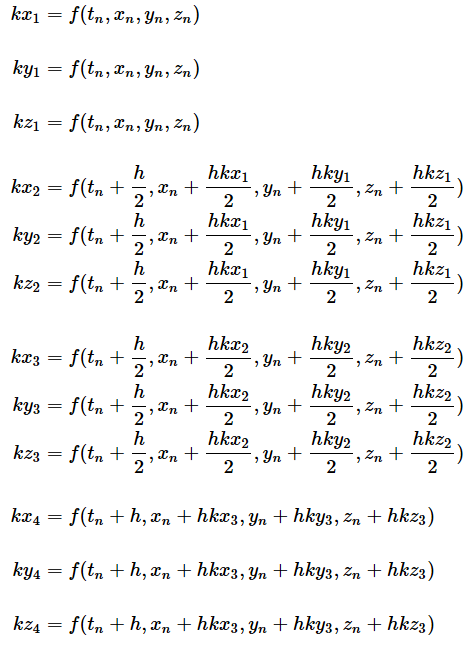微分法の数値計算をプログラミングしてみよう：数学×Pythonプログラミング入門（3/4 ページ）

微分法に関する数値計算のプログラミング方法を見ていく。最初に定義通りに計算する方法を、次に微分方程式を簡単に数値計算する方法を紹介。最後に、ルンゲ・クッタ法と呼ばれる精度のよい近似方法を見る。

[羽山博，著]

目標3： ルンゲ・クッタ法を使って微分方程式の数値計算を行う

　ルンゲ・クッタ法も、微分方程式の数値計算を行う方法ですが、精度のよい近似値が得られることが知られています。聞き慣れない名前かも知れませんが、複雑な計算が出てくるわけではなく、以下のように簡単な四則演算だけでできます。ここに示した式は、変数がxとyの2つの場合の例です。

のとき、

とし、

で、順に値を求めていきます。大まかなイメージは、x_nとx_n＋1の間を4つ（左右1つずつと中央2つ）に分けて、それぞれ微分係数（傾き）を求め、中央の2つの重みを大きくした平均の微分係数に、hを掛けて次のy_n＋1を求めているといった感じです。数学的にこれらの式を導き出すのはかなり難しいので、ここでは割愛しますが、計算の手順については後であらためて図解します。

　ルンゲ・クッタ法にいくつかの種類がありますが、ここに示したものは4次のルンゲ・クッタ法と呼ばれるもので、単にルンゲ・クッタ法と言うと、このような4次のルンゲ・クッタ法を指すのが一般的です。なお、「ルンゲ・クッタ」は、一人の人名ではなく、この方法を開発したカール・ルンゲ（Carl Runge）、マルティン・クッタ（Martin Kutta）という二人の数学者の名前です。

　ここでは、微分方程式の数値計算の例としてよく使われるローレンツの方程式を数値計算し、グラフを描くことを目標にしてみましょう。

　ローレンツの方程式は以下のような連立常微分方程式です。

　これらの微分方程式を元に、ルンゲ・クッタ法を使って、初期条件x＝y＝z＝1で関数f(x,y,z)の数値計算を行い、3Dグラフを描いてみると、以下のようになります。ここでは、hを0.01として、0から100（未満）まで変えながらグラフを描いてみました。

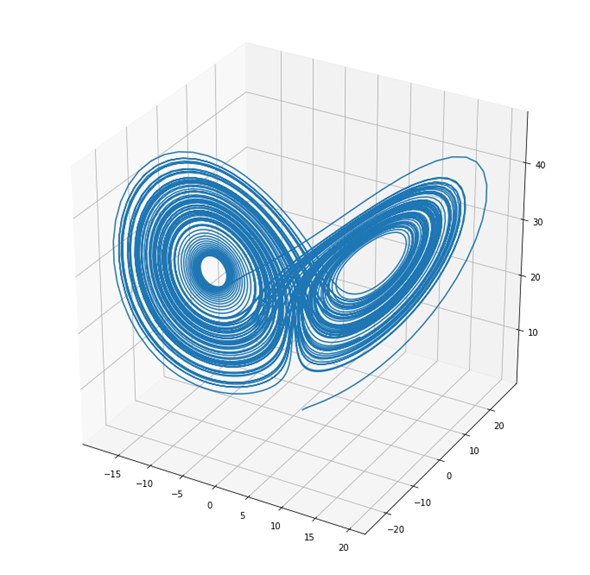
図5　ローレンツのアトラクタ
ローレンツの方程式を数値計算し、グラフを描くとこのような形になる（ローレンツのアトラクタと呼ばれる）。アトラクタとは、軌道を一定の範囲に引き込むような領域のこと。なお、ローレンツは「ソロモンの指輪」（早川書房）で有名な動物行動学者のコンラート・ローレンツ（Konrad Lorenz）ではなく、気象学者のエドワード・ローレンツ（Edward Lorenz）。

　ただ、いきなりローレンツの方程式に取り組むのはハードルが高すぎるので、その前に、目標2で見た簡単な例をルンゲ・クッタ法で数値計算してみるところからスタートします。まだイメージが湧かないという方もおられるかもしれませんが、この段階であーでもないこーでもないと考えるよりは、実際に数式をプログラムとして表していった方が、何をやっているかがよく分かります。とにかく（6）式に従ってコードを書いていきましょう。

4. 微分方程式の数値計算を行う（2） 〜 ルンゲ・クッタ法を使う

　目標2で見た微分方程式は以下のようなものでした。

　この式を表す関数dyは既に作成されていましたね。この関数は変数が1つだけなので、微分係数の計算にはxしか使わないのですが、目標のところに示した数式と形式を合わせるために、yも引数として書いておきます（リスト8）。

def dy(x, y):
  return x**2

リスト8　微分方程式を表す関数dy
既に見た関数dyと同じものだが、形式を合わせるためにyも引数として指定してある。

　（6）式を素直にPythonの関数として表してみましょう。リスト9のコードで、x、y、hを与えれば、kyが求められます。yがy_nの値に当たり、kyがy_n＋1の値に当たるというわけです。

def RungeKutta(x, y, h):
  k1 = dy(x, y)
  k2 = dy(x+h/2, y+h*k1/2)
  k3 = dy(x+h/2, y+h*k2/2)
  k4 = dy(x+h, y+h*k3)
  ky = y + h*(k1+2*k2+2*k3+k4)/6
  return ky

リスト9　y_nからy_n＋1を求める関数RungeKutta
（6）式をそのまま関数として表した。リスト8の関数dyと、このコードを見るとk1〜k4の計算にyの値が使われないので、（3）式の微分方程式を解くだけなら、ムダが多いように思える。しかし、2変数の場合にもこの関数RungeKuttaがそのまま使えるので、あえて1変数にせず、（6）式のままとした（後の練習問題で2変数の例を試してみましょう）。

　xの初期値を0、yの初期値を1とし、刻み値hを0.001として、関数RungeKuttaを呼び出し、リストに返り値を追加していけば、グラフ化のためのデータが作成できます。以下にそのコードを書いてみましょう（リスト10）。よく見ると、オイラー法のプログラムとほとんど同じで、数値計算を行う部分を関数RungeKuttaに置き換えただけだということが分かりますね。

import numpy as np
import matplotlib.pyplot as plt

y = [1] # 初期値
h = 0.001 # 刻み値

for x in np.arange(h, 2, h):
  y.append(RungeKutta(x, y[-1], h))

x = np.arange(0, 2, h) 
plt.plot(x, y) # ルンゲ・クッタ法で求めた値でグラフを描く
plt.plot(x, 13*x**3+1) # 解析的に求めた関数でもグラフを描く
plt.show()

リスト10　関数RungeKuttaを呼び出し、数値計算の結果をグラフ化する
ルンゲ・クッタ法を使って微分方程式の数値計算を行い、結果をグラフとして表示するためのコード。数値計算の部分が異なるだけで、データやグラフの作成方法はオイラー法とほとんど同じ。

　実行例もわずかな誤差の違いがあるだけで同じグラフになりますが、一応掲載しておきます（図6）。

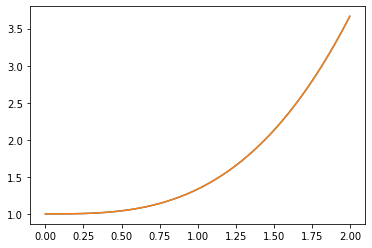
図6　ルンゲ・クッタ法を使って描いた微分方程式の解のグラフ（解析的に求めた結果と重ねて表示）
ブルーの線がルンゲ・クッタ法による解のグラフ、オレンジの線が解析的に求めた関数のグラフ。ほとんど一致するので、背後に表示されているブルーの線が隠されて見えなくなっている。

5. ローレンツの方程式のグラフを描く

　ルンゲ・クッタ法による数値計算のプログラミングができたので、いよいよローレンツの方程式のグラフを描いてみましょう。ローレンツの方程式は、以下のような、変数x, y, zをtで微分した連立常微分方程式でした。ルンゲ・クッタ法はこのような方程式の数値計算にも使えます。

　まず、これらの関数を定義しましょう。上の数式をそのままPythonの関数を使ったコードとして表すだけです（リスト11）。

def dx(t, x, y, z):
  return -10*x + 10*y

def dy(t, x, y, z):
  return -x*z + 28*x - y

def dz(t, x, y, z):
  return x*y - 83*z

リスト11　ローレンツの方程式を表す関数を書く
ローレンツの方程式をそのまま関数として表した。なお、-10、28、8/3といった係数を変えるとグラフの「ふるまい」が大きく変わる。いわゆるカオス理論の研究のさきがけとなった。

　あとは、ルンゲ・クッタ法で数値計算を行うための式に、これらの関数を全て当てはめるだけなのですが、変数が4つになり、微分方程式も3つあるので、式が少し多くなります。が、要領は同じです。微分方程式が、

である場合、

をそれぞれ求め、

を次々と求めていけばいいというわけです。では、コードを書いてみましょう（リスト12）。四則演算のみの単純な式ばかりですが、変数が多いので、間違えないように確実に入力していってください。

def RungeKutta(t, x, y, z, h):
  kx1 = dx(t, x, y, z)
  ky1 = dy(t, x, y, z)
  kz1 = dz(t, x, y, z)

  kx2 = dx(t+h/2, x+h*kx1/2, y+h*ky1/2, z+h*kz1/2)
  ky2 = dy(t+h/2, x+h*kx1/2, y+h*ky1/2, z+h*kz1/2)
  kz2 = dz(t+h/2, x+h*kx1/2, y+h*ky1/2, z+h*kz1/2)

  kx3 = dx(t+h/2, x+h*kx2/2, y+h*ky2/2, z+h*kz2/2)
  ky3 = dy(t+h/2, x+h*kx2/2, y+h*ky2/2, z+h*kz2/2)
  kz3 = dz(t+h/2, x+h*kx2/2, y+h*ky2/2, z+h*kz2/2)

  kx4 = dx(t+h, x+h*kx3, y+h*ky3, z+h*kz3)
  ky4 = dy(t+h, x+h*kx3, y+h*ky3, z+h*kz3)
  kz4 = dz(t+h, x+h*kx3, y+h*ky3, z+h*kz3)

  kx = x + h*(kx1+2*kx2+2*kx3+kx4)/6 # 次のx
  ky = y + h*(ky1+2*ky2+2*ky3+ky4)/6 # 次のy
  kz = z + h*(kz1+2*kz2+2*kz3+kz4)/6 # 次のz
  return kx, ky, kz

リスト12　x_n＋1,y_n＋1,z_n＋1の値を求める関数RungeKutta
ルンゲ・クッタ法により、関数dx／dy／dzを使って求めた微分係数にhを掛け、x_nからx_n＋1を、y_nからy_n＋1を、z_nからz_n＋1をそれぞれ求める。

　あとは、tの値を変えながら、この関数RungeKuttaを呼び出すだけです。

import numpy as np
import matplotlib.pyplot as plt

x = [1] # 初期値の設定
y = [1]
z = [1]
h = 0.01 # 刻み値

for t in np.arange(h, 100, h):
  xt, yt ,zt  = RungeKutta(t, x[-1], y[-1], z[-1], h)
  x.append(xt)
  y.append(yt)
  z.append(zt)

fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(projection='3d')
ax.plot(x, y, z)
plt.show()

リスト13　ローレンツのアトラクタを描画するコード
tの値を0〜100（未満）までとしてx_n＋1, y_n＋1, z_n＋1の値を次々と求めていく。あまり細かく刻むと、繰り返しの回数が増えるので、ここでは、刻み値hを0.01にした（繰り返し数は10000回となる）。

　実行結果は目標のところに掲載したものと同じです。実は、この例ではx、y、zをプロットすればいいので、特にtの値は使っていません。そこで、tをリストのインデックスとして使い、for文を以下のような単純な繰り返し処理にしても構いません（リスト14）。

for t in range(0, 10000):
  xt, yt ,zt  = RungeKutta(t, x[t], y[t], z[t], h)
  x.append(xt)
  y.append(yt)
  z.append(zt)

リスト14　y_nからy_n＋1を求める関数RungeKutta
tの値はグラフ化には使わないので、単純にインデックスとして扱い、繰り返しの回数を指定した。x[t], y[t], z[t]をx[-1], y[-1], z[-1]と書いても結果は同じ。

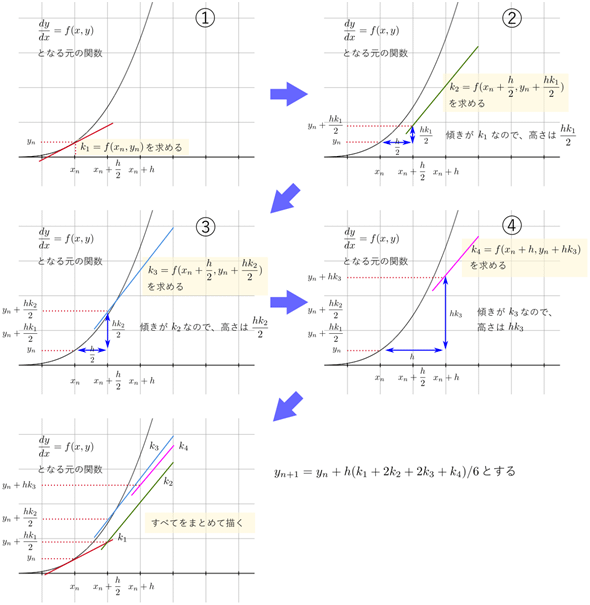
　以上でプログラムは完成です。数式をプログラミングしていく中で、処理のイメージは得られたでしょうか。次に、関数RungeKuttaの働きを図解するので、コードと照らし合わせながら、もう一度、処理の流れを確認しておいてください。

図7　ルンゲ・クッタ法による数値計算の仕組み
微分係数を4カ所で求め、真ん中の2つに重みを置いた平均の傾きに幅hを掛けて、高さを求め、y_nからy_n＋1を求めていくといったイメージ。

　図の番号と対応させて、説明します。

　最後の図は、（1）〜（4）までを1枚にまとめて書いただけです。これらの4つの微分係数について、中央の2つに重みを掛けて求めた平均の微分係数を使って「高さ」を求め、y_nからy_n＋1を求めます。