微分法の数値計算をプログラミングしてみよう:数学×Pythonプログラミング入門(2/4 ページ)
微分法に関する数値計算のプログラミング方法を見ていく。最初に定義通りに計算する方法を、次に微分方程式を簡単に数値計算する方法を紹介。最後に、ルンゲ・クッタ法と呼ばれる精度のよい近似方法を見る。
目標2: 微分方程式の数値計算を行う
今回の2つ目の目標は、微分方程式の数値計算です。微分方程式とは、方程式の中に導関数が含まれているものです。高校で学ぶものとしては、運動方程式が有名です(ただし、高校の物理では微分方程式の形では表現されていないかもしれません)。他にも放射性物質の崩壊や熱伝導など、変化を表すために、さまざまな分野で微分方程式が使われます。が、ここでは、数値計算の方法に集中するために、以下のような簡単な例を使って見ていきましょう。
まず、方程式の中に微分が含まれているということを確認してください。左辺が微分になっていますね。これは、関数y=f(x)をxで微分したものという意味です。右辺は単なるx2という式です。つまり、関数y=f(x)をxで微分したものがx2になっているということですね。
このような方程式を満たすような関数f(x)を求めることが微分方程式を解くということです。なお、独立変数xが1つで、その変数での微分が含まれている微分方程式を常微分方程式(じょうびぶんほうていしき)と呼び、多変数関数で、偏微分を含む場合は偏微分方程式と呼びます。
ところで、微分方程式が登場するまでの数学では、方程式の解は何らかの値でした。しかし、微分方程式の解は特定の値ではなく、関数になります。例えば、(3)式の解は、x=0のときにf(x)=1であるものとするなら、
という関数になります(なぜこのような結果になるのかは後で説明します)。ここでは、答えが簡単に分かるので(4)式を先に示しましたが、実際問題として微分方程式が上のように解けない場合があります。そのような場合に、元の微分方程式からxに対するf(x)の値を求めようというのが微分方程式の数値計算です。ここでは、(3)式の数値計算を行い、グラフを描くことにします。xの値を0〜2(未満)まで0.001刻みで変えながら、プロットすると図3のようなグラフになります。
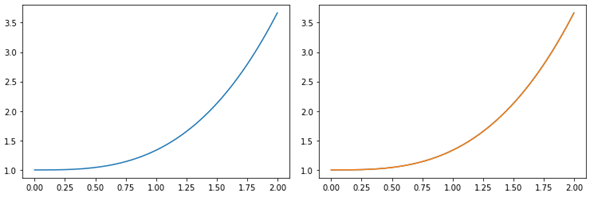
図3 微分方程式の解のグラフ
微分方程式の解は特定の値ではなく、関数になる。微分方程式の解き方を知らなくても、数値計算ができれば、簡単に左側のグラフが描ける。
右側のグラフは数値計算によるグラフ(ブルーの線)と、解析的に解いた関数(4)式のグラフ(オレンジの線)を重ねて描いたもの。やはり、ほとんど一致するので、背後に表示されているブルーの線が隠されて見えなくなっている。
微分方程式の解き方も、計算の方法も全く説明していないので、何だか難しそうだな、と思った方もおられるかもしれませんが、実は、目標1と同様、微分の定義さえ知っていれば、数値計算は簡単にできます。ただし、注意していただきたいのは、目標1は導関数を求めることがゴールでしたが、目標2は導関数が既に分かっているときに、その導関数を含んだ微分方程式の解となっている関数を求めるというのがゴールであるということです。
そこで、微分方程式がどのようなものであるかを理解し、雰囲気に慣れるために、上の微分方程式を解析的に解く方法をまず紹介しておきましょう。既に、微分方程式の解き方について学んだことのある方は、3章に進んでプログラミングに取り組んでみてください。
2. 簡単な微分方程式の解き方
微分方程式が目標のところに示したような形式(直接積分形と呼びます)の場合、微分と積分の関係を知っているなら簡単に解けます*3。ざっくり言うと、微分の逆の計算が積分、積分の逆の計算が微分でしたね。y=f(x)を微分するとx2になるわけですから、微分してx2になるような元の関数(原始関数)を求めればいいということになります。つまり、積分すればいいというわけです。
*3 他にも変数分離形や同次形などの表し方がありますが、ここでは、微分方程式の意味を知ることだけを狙いとしているので、これ以上は触れないことにします。
では、計算してみましょう。微分の場合は次数を1減らし、係数に次数を掛けたので、その逆の計算、つまり、次数を1増やし、係数に1/次数を掛ければオーケーです。ただし、微分の場合、定数項がいくらであっても消えてしまうので、どんな値であったかを決めることはできませんが、定数項を付け加えておく必要があります。従って、
を積分するのであれば、次数の2を1つ増やして3にし、1/次数を係数に掛けるといいですね。定数項をCとすると、
のようになります。これで、微分方程式が解けました。整理しておくと、
の解は、
という関数になるというわけです。Cの値が決まっておらず、一般的な表し方になっているので、このような解のことを一般解と呼びます。
ここで、x=0のとき、f(x)の値を1とする、というように初期条件を決めてやると、
なので、Cの値が1と決まります。つまり、この場合の解は、
となり、関数が一意に決まります。このような解のことを特殊解と呼びます。
微分方程式がどのようなものであるか、イメージはつかめたでしょうか。数値計算を行うには、上のような式の変形は不要なのですが、やり方を知るだけよりは、微分方程式の意味が多少なりとも分かっておいた方がいいので、解説を加えておきました。では、続いて微分方程式を解くための数値計算に取り組みましょう。
3. 微分方程式の数値計算を行う(1) 〜 オイラー法を使う
以下の方法はオイラー法と呼ばれる数値計算の方法ですが、既に述べたように、微分の定義が分かっていれば、簡単に微分方程式の数値計算ができます(またまたオイラーさんが登場しましたね)。おさらいがてら、微分の定義からはじめて、その方法を見ていくことにします。微分(導関数)の定義は以下のようなものでした。
でした。hが十分小さいのであれば、
で近似できることも、目標1で見た通りです。微分方程式を解くということは、関数f(x)を求めるということですね。つまりf(x)の値を次々と求めていけば、関数f(x)がどのような式で表されるかが分からなくても、数値計算はできますし、グラフも描けます。そこで、この式を少し変形しましょう。まず、両辺にhを掛けると、以下のようになります。
続いて、f(x)を左辺に移項しましょう。
左辺と右辺を入れ替えると、以下のようになります。
この式を使えば、右辺のf(x)とhとf'(x)を基に、左辺のf(x+h)の値が求められます。f(0)=1と初期条件を決めておけば、h=0.01、f'(x)=x2を利用して、f(x+h)の値が求められます。これを次のf(x)にして、xの値をhずつ増やしていけば、次々とf(x+h)の値が求められます。以下の表に、この方法で計算した結果を先頭から5つだけ書いておきました。
| x 初期値は0で、0.01ずつ増える |
f(x) … (1) 初期値は1 |
h … (2) 刻み値 |
f'(x) … (3) x2の値 |
f(x)+hf'(x) … (1)+(2)×(3) f(x+h)の値……次のf(x)となる |
|---|---|---|---|---|
| 0 | 1 | 0.01 | 0 | 1 |
| 0.01 | 1 | 0.01 | 0.0001 | 1.000001 |
| 0.02 | 1.000001 | 0.01 | 0.0004 | 1.000005 |
| 0.03 | 1.000005 | 0.01 | 0.0009 | 1.000014 |
| 0.04 | 1.000014 | 0.01 | 0.0016 | 1.000030 |
(5)式を計算していくとこのような結果になる。右端の値がf(x+h)値になる。これらの値をプロットしていけば、微分方程式の解がグラフ化できることが分かる。
以上のことから、(5)式の計算を行い、f(x+h)、つまり、f(x)+hf'(x)の値を次々と求めていけばいいということが分かりますね。
いや、数式だけではどうもイメージが湧かないという方は、図4の図解を参照してみてください。動画での解説も用意してあるので、順を追って確認したい方はそちらもご利用ください。なお、数式と表1だけで十分理解できたという方は、図解は飛ばしてプログラミングに取り組んでいただいてけっこうです。
動画3 オイラー法による数値計算の仕組み
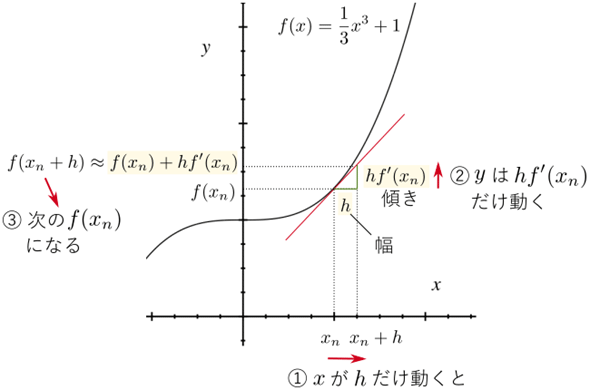
図4 オイラー法による数値計算の仕組み
「幅×傾き=高さ」なので、幅がh、傾きがf'(xn)なら、高さはhf'(xn)となる。つまり、xをxnからhだけ動かすと、yはf(xn)からhf'(xn)だけ動く。hは小さな値なので、f(xn+h)は、f(xn)に「高さ」を足した値、つまり、f(xn)+hf'(xn)で近似できる。f(xn+h)を次のf(xn)として、この操作を繰り返せば、次々とf(xn)の値が求められる。
例えば、x0=0,f(x0)=1といった初期条件を決め、そこを出発点として、図4のような操作を繰り返し、f(xn)の値を次々と求めていくというわけです。いかがでしょう。微分方程式を満たす関数の値が、(数式としては求められませんが、数値として)求められることがイメージできたでしょうか。
ちょっとした例え話ですが、皆さんが図4のような世界に転生し、回りが真っ暗な所で、グラフと接線の接する点に立っているという状況を想像してみてください。大きく動くと足を踏み外して谷底に落ちてしまいますが、ほんのわずか先が見えれば少しだけ先に進めますね。時間はかかりますが、そのようにして手探りで進めば、接線に沿って歩いて行けます。初期条件は、転生したときに最初にいた場所に当たりますね。正確さには欠けますが、そういった身体的なイメージで捉えてもらってもいいかと思います。
では、コードを書いてみましょう(リスト6)。まず、微分方程式を表す関数dyを作っておきます。これは簡単です。
def dy(x):
return x**2
微分方程式をそのまま書くだけなので簡単。returnの後の式を変えれば、さまざまな微分方程式が表せる。
あとは、(5)式の計算です。Pythonの関数にしてもいいのですが、f(x)+hf'(x)の値を求めるだけなのでそのまま書くことにします。xの値はhずつ増やしていけばいいですね(リスト7)。
y = [1] # 初期値
h = 0.01 # 刻み値
for x in np.arange(h, 2, h): # x=0のときy=1と初期条件を決めたのでx=0.01から
y.append(y[-1] + h*dy(x)) # y[-1]は直前に追加したyの(末尾の)値
x = np.arange(0, 2, h)
plt.plot(x, y) # 数値計算でグラフを描く
plt.plot(x, 13*x**3+1) # 解析的に求めた関数でもグラフを描く
plt.show()
オイラー法を使って微分方程式の数値計算を行い、グラフを表示する。append関数の引数として指定した式が(5)式に当たる。初期値だけ特別扱いしたので、繰り返しは0からではなくhから始める。なお、y[-1]のように、インデックスに-1を指定すると、最後の要素(直前に追加した要素)を取り出せる。
実行結果は目標のところに示した図3の右側のようになります。ここに至るまでは長かったですが、コードは思った以上に簡単でしたね。これで目標2がクリアできました。
続けて、微分方程式の数値計算を行うためによく使われるルンゲ・クッタ法も紹介しておきます。
Copyright© Digital Advantage Corp. All Rights Reserved.