Titanicから始めよう:データを可視化して、EDAのまねごとをしてみた:僕たちのKaggle挑戦記
今回はseabornライブラリを使用して、Titanicデータセットの各列が生死とどのような関係にあるかを(少しだけ)確認してみました。それだけで、スコアはアップ!
前回は、Kaggleのコンペティションに初参加ということで、皆さんの多くが手始めに触るであろうTitanicコンペティションに自分も参加して、取りあえずデータをDNN(Deep Neural Network)に突っ込んでみました。その後、コードの再利用を念頭に置いたプログラムの構造化というちょっとズレた方向に進んだり、k-fold交差検証をしたりしてみました。
今回はちょっと方向性をまた変えて、探索的データ分析(Explanatory Data Analysis、EDA)の初歩の初歩を体験してみることにしました。seabornというデータ視覚化ライブラリを使用して、Titanicのデータを少々分析して、その結果から、テストデータのSurvived列の値を推測するという感じです。
前回に最後に触れた「PyTorchのrandom_split関数があれば、scikit-learnのKFoldクラスを使わずとも、K-fold交差検証を行うコードを書けるんじゃないか」という話についても最後に簡単に触れようかなぁ。結果だけいえばできるんですが、まあだからナニ? という話にしかなりませんでした(笑)。[かわさき]
PyTorchで交差検証するときも、scikit-learnのKFoldクラスを使うのが一般的なのですかね。Google検索したらそのサンプルコードばかりヒットしたので。[一色]
本稿の最後に示すget_kfold_datasets2関数のコードに出てくるように、(random_split関数などを使って)データセットを複数のSubsetクラスのインスタンスに分割して、それらをConcatDatasetクラスでまとめるという方法もあるみたいです。
まずは今回のスコアの変遷について、まとめておきます。以下のスコアは前回に作成したDNNのようなモデルを使わずに、EDAから得られたデータ特性を基に「○○という条件の下では××の生死はこうなる」ということをそのままベタに予測して得られたものです。
| 条件 | スコア |
|---|---|
| 女性は全員生存/男性は全員死亡 | 0.76555 |
| 女性は全員生存/男性で旅客運賃のレンジが一番上の人は生存 | 0.76555 |
| 女性は全員生存/男性で年齢のレンジが最小または最大の人は生存 | 0.76794 |
| 旅客クラスが3、出港地が'S'の女性は死亡 | 0.77990 |
スコアは正解率なので1.0に近いほど良いです。
探索的データ分析とは
探索的データ分析を簡単にまとめると「何らかの課題を解決するためにそろえられたデータから、それらがどんな意味を持つのか、本当に必要なデータは何か、課題を解決する上で無視すべきデータ(外れ値)はどれか、データにどんな相関が見られるか」などの情報を見いだすことといえます。
Titanicコンペであれば、以下のようなデータがそろえられています。
- PassengerId:コンペ用に割り当てられた乗客ID。独自に割り当てられたものなので生死とは直接は関係ない
- Survival:生死情報(0:死亡、1:生存)。学習する際には教師データとして使われ、EDAを行う際には各種データがこの値とどんな関係にあるかを調べていく
- Pclass:旅客クラス。1が1等、2が2等、3が3等(1が高級で、3が下級)
- Name:乗客の名前。たぶん、生死とは直接は関係ない
- Sex:性別('male'か'female')
- Age:年齢(浮動小数点数値)
- Sibsp:Titanic号に同時に乗船している兄弟や配偶者の数
- Parch:Titanic号に同時に乗船している親や子どもの数
- Ticket:チケット番号。これもたぶん、生死とは直接は関係ない
- Fare:旅客運賃
- Cabin:部屋番号。これも生死とは直接は関係ないかもしれない
- Embarked:乗船した港('S'、'C'、'Q')
Kaggleではこうした情報が事前にまとめられていることもあれば、そうではないこともあるようです。Titanicコンペであれば、コンペページの[Data]タブにこうした情報がまとめられています。
以下では、このデータセットをざっくりと眺めてみることにしましょう。
各列の相関とヒートマップの表示
ここではpandasを使ってTitanicのデータセット(CSVファイル)を読み込んでいます。その後、上で「直接は関係ない」と述べた列を削除しています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df0 = pd.read_csv('../input/titanic/train.csv')
droprows = ['PassengerId', 'Name', 'Ticket', 'Cabin']
df0 = df0.drop(droprows, axis=1)
この後に何をすればよいかと考えましたが、まずは各列が生死情報とどの程度の相関を持っているかを計算してみることにしました。というと難しそうですが、実際にはpandasのデータフレームが持つcorrメソッドを呼び出すだけです。
df1 = df0.replace('male', 0).replace('female', 1)
df1 = df1.replace('S', 0).replace('C', 1).replace('Q', 2)
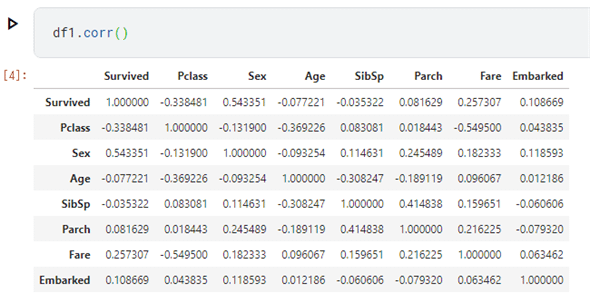
df1.corr()
注意したいのは、corrメソッドは数値型の値だけを対象とすることと、欠損値があればその値は無視されることです。上のコードで、'male'や'female'あるいは'S'や'C'などの値を数値に置き換えているのはこのためです。また、ここでは欠損値については無視しています。
欠損値については、それをDNNに入力するようなときには何らかの形で対応する必要がありますが、今回はそこまでたどり着いていないので、無視したままとしましょう。
これを実行した結果が以下です。
各列の相関関係はこれを見ても分かりますが、より分かりやすくするにはseabornのheatmap関数を使うとよいようです。
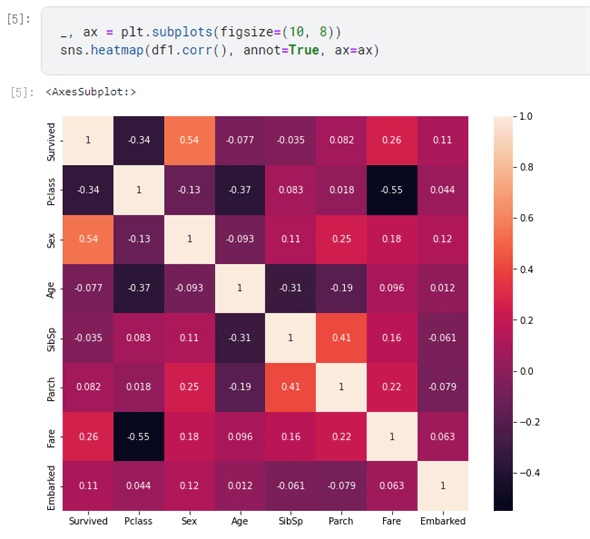
_, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(df1.corr(), annot=True, ax=ax)
1行目は表示領域の指定で、2行目が実際にヒートマップを表示するコードとなっています(annot=Trueを指定すると、上の画像に表示されていた数値群がヒートマップにも表示されます)。
相関関係が色を使って分かりやすく表示されました。右側のバーを見ると分かる通り、相関関係相関関係は黒(負の相関)〜赤紫(無相関)〜クリーム色(正の相関)のようになっています。そして、生死情報に関連する項目を知りたいのですから、注目すべきは一番上の行(Survived行)でしょう。パッと見には、オレンジ色で表示されているSex列と、明るめの赤で表示されているFare列の相関が強そうです。まずは性別の違いが生死にどう関係しているかを確認してみましょう。
Titanic号からは女性と子どもが優先して脱出したという話を聞いたことがあるので、年齢がそれほど強く出てこないのが意外でした。
おお ! 確かにSex列とFare列は正の相関が高いですね。でもPclass列は負の相関が高いので、こちらも確認した方がよかったかもと思いました。
このように相関を可視化すれば、有効な特徴量が分かりやすいですね。これは必須な作業だと思えました。今度やろう。
性別による生死の違い
ここではseabornのcatplot関数を使って、男女で生死がどう違っているかをプロットしました。
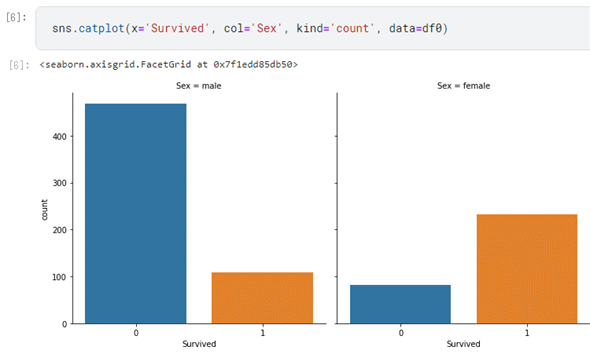
sns.catplot(x='Survived', col='Sex', kind='count', data=df0)
その結果は以下の通りです。
大きく分けて、左側が男性の死者数と生存者数、右側が女性の死者数と生存者数です。一目で女性の生前率の方が高いことが分かりますね。そこで、テストデータに対して、女性が全員生存、男性は全員死亡と予測して、その結果を保存、提出してみました。
dft = pd.read_csv('../input/titanic/test.csv')
dft['Survived'] = dft['Sex'] == 'female'
dft['Survived'] = dft['Survived'].astype(int)
dft[['PassengerId', 'Survived']].to_csv('onlygender_submission.csv', index=False)
この予測のスコアはなんと「0.76555」でした。前回のモデル4(3種類のモデルを使って、K-fold交差検証を行ったもの)のスコアが「0.76794」だったことを考えると、たったこれだけのことでそこまでのスコアが出てしまうというのが……。
むやみやたらとDNNに突っ込んでみる方針がいとも簡単に否定された(笑)。データの分析と前処理はきちんとやらないとダメってことですね。
うんうん。やっぱり探索的データ分析とか特徴量選択とか特徴量エンジニアリングとか機械学習では大切だな、と実感できます。
ところで、この結果をもって「Titanicの機械学習では、性別(Sex)の特徴量を使った方がいい」という理解でいいのかな?
次回にそれは考えることにしましょう。指摘のあったPclassなど、ちゃんと話に上がってきていないものもありますし。この後出てくる連続量の離散化など以外にもまだやることはあるっぽいので(ぐっ)。
旅客運賃
次に旅客運賃の差が、生存率にどのように関連しているかを見てみます。高いお金を払ったお客さんが優先して救助されていそうな気はしますね。ただし、その前に旅客運賃の範囲を調べておく必要があるでしょう。
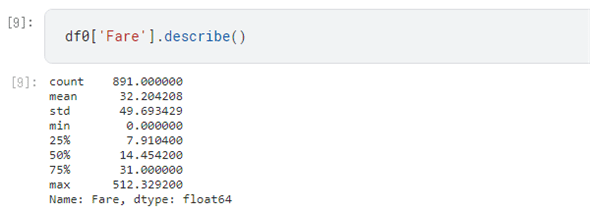
df0['Fare'].describe()
このコードを実行すると、以下のような出力が表示されます。
ここからはデータ数、平均、標準偏差、最小値、最大値などの情報が得られます。ここでは最小値と最大値を知ることを目的でした。また、以下のコードでデータの分布を確認できます。
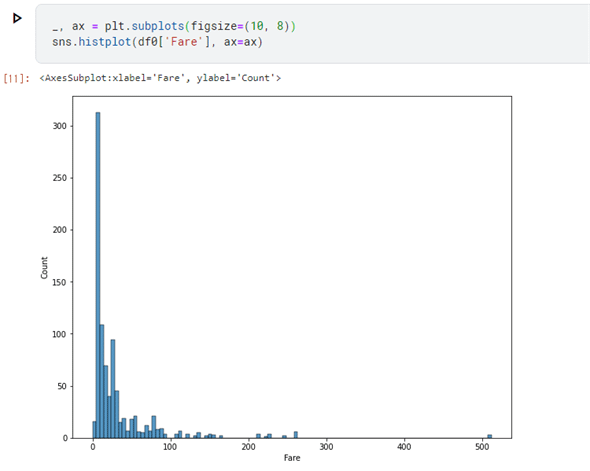
sns.histplot(df0['Fare'])
実行結果は以下の通りです。
運賃は低い方に集中して、高い運賃を支払った人は少ないようです。ところで、この分布が生存率とどの程度関係しているかを調べるには、少し工夫が必要です。運賃は連続する浮動小数点数値なので、それらの値を価格帯ごとにまとめた方がよいでしょう。
ビニング(binning:ビンにグループ化)とか離散化(discretization)とか言われている特徴量エンジニアリングのテクニックですよね。
ここでは、以下のコードでこれを行っています。
df1 = df0.copy()
df1['Fare_range']=np.nan
fare_range = [n * 50 for n in range(11)]
for idx, num in enumerate(fare_range):
df1.loc[df1['Fare'] >= num, 'Fare_range'] = idx
この状態で先ほどと同様に分布を調べると次のような結果になりました。
価格帯ごと(加えて性別ごと)に生死情報をプロットするコードは以下のようになります。
sns.catplot(x='Survived', col='Fare_range', kind='count', data=df1, col_wrap=3)
実行結果は次の通りです。
ここでも女性の生存率が圧倒的に高い結果となってしまいました。たぶん、少し別の尺度を用いないと、常にこれに似た結果になってしまいそうです。強いていうと、上の画像にはありませんが、高い運賃を払っている層では(わずかではありますが)男性の生存者がいることが分かります。そこで、これを反映して、推測をしてみることにしましょう。
dft['Fare_range']=np.nan
fare_range = [n * 50 for n in range(11)]
for idx, num in enumerate(fare_range):
dft.loc[dft['Fare'] >= num, 'Fare_range'] = idx
dft.loc[(dft.Sex == 'male') & (dft.Fare_range == 10)] = 1
dft['Survived'] = dft['Survived'].astype(int)
dft[['PassengerId', 'Survived']].to_csv('sex_fare_submission.csv', index=False)
ですが、テストデータではそうした乗客がいなかったため、スコアは変わらずという結果になってしまいました。
事前にテストデータにそうしたデータが存在するかを確認すべきでした。
そもそも高い運賃を払った人がtrainデータでも数として少ないみたいなので、機械学習時もあまり影響がなさそうな気がしますね。
前掲の図の分布にも左側に大きな偏りがあるので、ビニングの前に正規分布に近くなるような変換を行うと、機械学習するのに有効な特徴量になるのかなと思いました。
どうような方法で年齢を10歳区切りで分割して、そのそれぞれで生死がどうなっているかを確認し、生存率が高そうな(男性の)乗客を調べることもできるでしょう。あるいは、ここでは取り上げなかった別の項目(Pclassなど)と組み合わせることで、新たな知見を得ることもできるでしょう(これらについても少しだけコードがあるので、公開しているノートブックを参照してください)。
前回に筆者は「0.76794」というスコアを出すのにアレコレとやってみたのですが、今回は最終的にほんの少しデータを分析するだけで「0.77990」とあっさりと更新してしまったのです(あらら)。
おまけ:random_split関数を使ってK-fold交差検証するためのコード
前回はtorch.utils.data.random_split関数の第2引数には、分割後のオブジェクトの要素数を3つ以上指定できるので、これを使えば、K-fold交差検証を行うコードをscikit-learnのKFoldクラスを使わなくても書けるのでは、という話をしました。冒頭でも述べたように、これは実際に可能でした。詳細は省略しますが、コードだけを以下に示します。この関数は、データセットと分割数を受け取り、分割したデータセットから訓練データと検証データを組み立て、それらを要素とするタプルを格納するリストを返すものです。
def get_kfold_datasets2(dataset, k):
random.seed(2)
if k < 3:
raise ValueError('k should be larger than 2.')
if not hasattr(dataset, '__len__'):
raise TypeError(f'{dataset} does not have a __len__ attr')
else:
ds_length = len(dataset) # ok since dataset has a __len__ attr
quotient = ds_length // k
remainder = ds_length % k
split_nums = [quotient] * k
for idx in range(remainder):
split_nums[idx] += 1
#simple: split_nums[:remainder] = [quotient+1] * remainder
tmp_datasets = random_split(dataset, split_nums)
datasets = []
for idx in range(k):
train_ds = tmp_datasets.copy()
val_ds = train_ds[idx]
del train_ds[idx]
train_ds = ConcatDataset(train_ds)
datasets.append((train_ds, val_ds))
return datasets
ほんとうはこのコードをネタとして話をする予定でしたが、random_split関数がコード中に埋没して、「確かに分割できるよねぇ」程度の話にしかなりそうもなかったのでこんな扱いになってしまったのでした(泣)。
Copyright© Digital Advantage Corp. All Rights Reserved.