積分法の数値計算をプログラミングしてみよう：数学×Pythonプログラミング入門（4/5 ページ）

積分法に関する数値計算のプログラミングの方法を見ていく。最初に台形公式やシンプソンの公式を使った方法を紹介し、次に乱数を使ったモンテカルロ法による近似方法を見る。

[羽山博，著]

目標4： モンテカルロ法により標準正規分布のサンプリングを行う

　モンテカルロ法は積分（面積）を求めるためだけに使われるわけではなく、サンプリングのためにも使われます。ここでは、標準正規分布に従ってサンプリングを行う例を見てみましょう。

　標準正規分布の確率密度関数は、平均値μが0、標準偏差σが1の正規分布で、以下のような式で表されます。

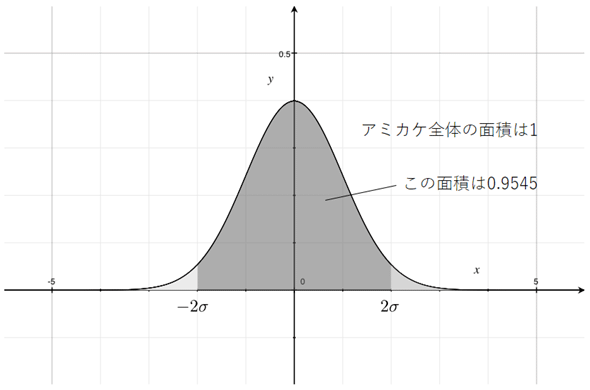
　標準正規分布のグラフを描くと以下のようになります。標準正規分布の定義域は−∞から∞までで、アミカケの部分の面積は1になります。また、−2σ〜2σの範囲の面積（濃いアミカケ部分の面積）は0.9545です。

図6　標準正規分布では全体の面積（確率）が1となる
標準正規分布の定義域は−∞から∞まで。yの最大値はx＝0のときなので、（2）式のxに0を代入して求めた値（0.3989）となる。全体の面積は1。

　というわけで、モンテカルロ法により、アミカケ全体に入る点のx座標値を数多く取り出す（サンプリングする）関数monte_mksampleを作成してください。mksampleの引数は以下のように指定するものとします。

mksample(func, xmin, xmax, ymin, ymax, n)

• func ……　サンプリングを行う対象の関数（ここでは標準正規分布の確率密度関数を指定する）
• xmin ……　xの定義域の下限値
• xmax ……　xの定義域の上限値
• ymin ……　yの値域の下限値
• ymax ……　yの値域の上限値
• n ……　繰り返し数

　関数monte_mksampleの返り値はサンプリングされた点のx座標値のリストとします。このリストの値をヒストグラムにすれば、図6に示したグラフに近い形になります。また、そのリストを使えば−nσ〜nσ,(n＝1,2,3,...)の範囲に入る確率を求めることもできます。目標3で見た方法は四角形の面積の中でどれだけの割合を占めているかを求めましたが、こちらでは、アミカケ全体に入った点の中で、−nσ〜nσの範囲に入っている点の個数の割合を求めます。例えば、−2σ〜2σに入る確率（0.9545...の近似値）を求めてみましょう。

4. モンテカルロ法によるサンプリングをプログラムとして表す

　まず、標準正規分布を関数stdnormとして定義します。（2）式の確認を兼ねて、穴埋め（ア／イ／ウ）にした以下のコードを完成させてください。

import numpy as np

def stdnorm(x):
  return 1ア(2*np.イ) * np.ウ(-(x**22))

リスト19　標準正規分布の確率密度関数を定義する
（2）式で表される標準正規分布の確率密度関数を素直に表現したもの。

（答え）オレンジ色の部分をクリックすると答えが表示されます。

• ア. 　sqrt　
• イ. 　pi　
• ウ. 　exp　

　続いて、関数monte_mksampleを作成します（リスト20）。これは、前ページに掲載したリスト12の関数monteを改造すればできます。異なる点は、乱数の下限値と上限値を指定できるnp.random.uniform関数を使うことと、アミカケの範囲に入る点のx座標を全て記録して返すことです。個数を数える必要はありません。

import numpy as np

def monte_mksample(func, xmin, xmax, ymin, ymax, n):
  np.random.seed(0)
  data = [] # アミカケ部分に入ったxを記録するためのリスト
  for i in range(n):
    x = np.random.uniform(xmin, xmax) # xminからxmaxまでの一様乱数
    y = np.random.uniform(ymin, ymax)
    if y < func(x):
      data.append(x)
  return data

リスト20　任意の関数のサンプリングを行う関数monte_mksampleを定義する
y＝x²を積分する例では、xの範囲が0〜1、yの範囲も0〜1と決まっていたので、0以上1未満の乱数を返すnp.random.random関数をそのまま使ったが、ここでは、np.random.uniform関数を使って、下限値以上、上限値未満の乱数を作る。

　なお、random.uniform関数でも、作成する乱数の個数を指定できます。例えば、np.random.unform(0, 10, 5)とすれば、0以上10未満の浮動小数点数の乱数を5個返してくれます。従って、前ページに掲載したコラムで述べたような繰り返し処理を使わない方法でもコードを書くことができます。しかし、ここでは処理の流れが見えるようにするため、繰り返し処理を使って話を進めます。

　標準正規分布では、xの定義域は−∞〜∞ですが、その範囲の一様乱数を作ることはできないので、xの範囲を-6〜6に限定して実行してみましょう。正規分布では、−6σ〜6σの範囲に99.999999％の点が存在するので、この範囲外は無視しても差し支えないだろうというわけです。

　また、標準正規分布では、yの値域は最小値が0で、最大値がx＝0のときのyの値です。従って、yの範囲は0〜stdnorm(0)とします。

　xとyの定義域を指定して関数monte_mksampleを呼び出しているのがリスト21です。

ymax = stdnorm(0) # x=0のときyは最大となる
data = monte_mksample(stdnorm, -6, 6, 0, ymax, 100000)

リスト21　標準正規分布のサンプリングを行う
−6σ〜6σの範囲で、アミカケの部分に入る点のx座標値が全て求められ、dataに代入される。標準正規分布ではσ＝1なので、下限値として-6を、上限値として6を指定した。

　返り値のdataを基にヒストグラムを作成するコードは以下の通りです。図7はその実行例です。

import matplotlib.pyplot as plt
import numpy as np

# ヒストグラムの作成
plt.hist(data, bins=100, density=True)

# 標準正規分布のグラフを重ねる
xrange = np.arange(-6, 6, 0.01)
y = [stdnorm(x) for x in xrange]
plt.plot(xrange, y)

plt.show()

リスト22　標準正規分布のヒストグラムを作成する
アミカケの範囲に入ったxの個数をヒストグラムにする。hist関数では、引数binsに階級の個数を指定する。また、引数にdensity=Trueを指定すると、縦軸の目盛りが個数ではなく確率になるようにグラフが表示される。

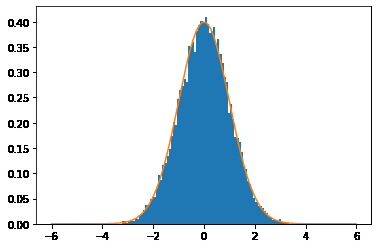
図7　乱数を使って作成したヒストグラムと標準正規分布のグラフ
ブルーの部分がサンプリングされたデータをヒストグラムにしたもの。オレンジの線は標準正規分布の確率密度関数のグラフ。ややギクシャクしているところはあるが、ヒストグラムと元の関数を使って描画したグラフがほぼ重なっていることが分かる。

　続いて、−2σ〜2σに入る確率も求めてみましょう。これは、アミカケの中に入った点のx座標値全体（data）のうち、 −2 ≤ x < 2となる点の個数を全体の個数で割れば求められますね（定義域の範囲の指定方法に合わせて-2以上2未満としました）。繰り返し処理を使って、全ての要素をチェックして個数を数える方法もありますが、ここはNumPyのcount_nonzero関数を使って一気に答えを求めましょう（リスト23）。

import numpy as np

x = np.array(data) # dataをNumPyの配列にしておく
np.count_nonzero((-2 <= x) & (x < 2)) / len(x)
# 出力例：0.9539577269907915

リスト23　標準正規分布の−2σ〜2σに入る確率を求める
NumPyのcount_nonzero関数は前ページに掲載したコラムで紹介したもので、ここでは(-2 <= x) & (x < 2)で求められる配列の要素のうちTrueの個数を数えるのに使っている（この部分は-2 <= x < 2とは書けないことに注意）。なお、−2σ〜2σに入る正確な確率は0.9545...なので、誤差は0.0005程度となっている。

　モンテカルロ法は簡単な方法ですが、関数（例：標準正規分布の確率密度関数）によっては、繰り返しの回数を増やしてもサンプリングされるデータの個数が増えないという問題があります。上の例では、−6σ〜6σというかなり狭い範囲でサンプリングしているにもかかわらず、取り出されるデータの個数は20959個しかありません（len(x)の値です）。ヒストグラムが少しギクシャクした感じになっていたのは階級の数に比べてサンプリングされたデータが少ないからです。

　さらに、−10σ〜10σの範囲でサンプリングすれば12575個、−100σ〜100σの範囲だとたったの1273個しかデータが取り出せません（リスト21でxminとxmaxの値を変えて実行し、リスト23のlen(x)を求めてみればそれらの値が求められます）。10万回の繰り返しで作られたデータのうち、約99％のデータが使われないのはムダが多すぎますね。

　かといって、多くのサンプルを得るために繰り返し数を増やすわけにもいきません。ムダな計算のために時間が掛かりすぎてしまい、実用に供せなくなってしまうからです。そこで、積分に寄与する値を重点的に取り出す方法として、マルコフ連鎖モンテカルロ法などが使われます。やや発展的な内容になりますが、そのアルゴリズムの1つであるメトロポリス法を次ページの練習問題で取り上げることにします。