積分法の数値計算をプログラミングしてみよう:数学×Pythonプログラミング入門(5/5 ページ)
積分法に関する数値計算のプログラミングの方法を見ていく。最初に台形公式やシンプソンの公式を使った方法を紹介し、次に乱数を使ったモンテカルロ法による近似方法を見る。
練習問題
それでは、練習問題に取り組み、ここまで見てきた数値計算の方法を確実に身に付けましょう。練習問題についても、プログラムの作成例と実行例を動画で紹介しています。解答例のコードについては、1行ずつ細かく解説することはしていませんが、大きな流れをつかむためにぜひ参照してみてください。
動画2 積分法の数値計算の練習問題
(1)台形公式とシンプソンの公式で標準正規分布の累積確率を求める
正規分布では、μ − 2σからμ + 2σまでの範囲の累積確率は95.4%となっています(μは平均、σは標準偏差)。台形公式とシンプソンの公式を使って、μ=0、σ=1の標準正規分布のμ − 2σからμ + 2σまでの範囲の累積確率を求めてみてください。刻み値は0.001として計算してみましょう。小数点以下15桁まで正確に求めると0.954499736103642となるので、誤差がどれくらいになるか比較してみてください(これまでのサンプルプログラムを単に実行するだけでできます)。
(2)曲線の長さを求める
曲線y=f(x)の、x=aからx=bまでの長さLは以下の式で求められます。
例えば、y=x2のx=0から1までの曲線の場合、
なので、
となり、この答えは1.4789428575445974...になります。この定積分の値を求めるために台形公式やシンプソンの公式を使ってもいいのですが、ここでは、xとyの微小な値とピタゴラスの定理を使って曲線の長さを求めることにしましょう(方法は後述のヒントを参照)。そのような関数linelengthを作成してください。実行例は以下の通りです。
linelength(parabolic, 0, 1, 0.0001)
# 出力例:1.4789428567991607
parabolicはリスト1で作成したy=x2の値を返す関数。始点を0、終点を1、刻み値を0.0001とした。
(ヒント)
以下の図8で、xの微小な値をΔ x、yの微小な値をΔ yとすれば、三角形の斜辺の長さはピタゴラスの定理により、
となります。この長さを足し合わせていけば、曲線の長さの近似値が求められるはずです。
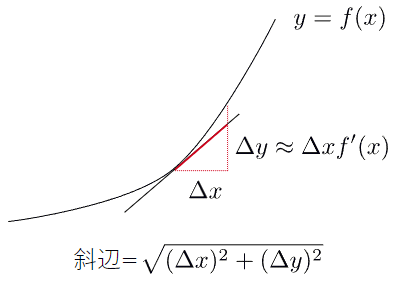
図8 曲線の長さを三角形の斜辺で近似する
Δxに微分係数を掛けると高さΔyが求められる。Δxがごく小さい値であれば、斜辺の長さがほぼ曲線の長さと等しい。斜辺の長さはピタゴラスの定理で求められる。この微小な斜辺の長さを足していけば、曲線の長さが近似できる。
xを0.0001刻みで増やしながら、斜辺の長さを足していき、1.4789428575445974...に近い値が得られれば正解です。Δ yの値は、刻み値×微分係数で求められます。微分係数を求めるには、前回使った関数derivative(リスト25)を利用するといいでしょう(ちょっとしたおさらいですね)。
def derivative(f, x, h):
return (f(x+h) - f(x)) / h
fには関数の参照を指定し、hには刻み値を指定すればよい。この関数が返す値と刻み値の積がΔ yになる。
(3)マルコフ連鎖モンテカルロ法により標準正規分布のサンプリングを行う
マルコフ連鎖とは、直前の状態からのみ、次の状態がある確率で決まるような連鎖のことです。典型的なものとしては、ランダムウォークが有名です。時間tに位置yにいた人が、時間t+1には1/2の確率でy+Δ yまたはy−Δ yに移動するといった例ですね。時間tから時間t+1に移動する確率は、それより以前からの影響は受けないというものです。
マルコフ連鎖モンテカルロ法(以下MCMCと略します)では、マルコフ連鎖を利用して、次々と値を作成していく方法です。それにより、出現確率の高い値(グラフの山の部分に近いxの値)を重点的に採用し、単純なモンテカルロ法よりも少ない繰り返し数で、効率よくデータをサンプリングします。ベイズ統計で事後分布を求める場合、その計算を解析的に行うのは難しくなります。しかし、MCMCを利用すれば簡単に事後分布が得られます。なお、目標4で見た例では、−6σ〜6σの範囲外は無視していましたが、そのような値も「たまに」サンプリングされるようになっています。
ここでは、メトロポリス法と呼ばれるアルゴリズムを紹介するので、それに従ってコードを書いてみてください(MCMCについての詳しい話は『ゼロからできるMCMC』(花田政範・松浦荘著、講談社)などを参照していただくといいでしょう)。アルゴリズムは以下の通りです。
- Δ xの値をランダムに決める
- xt+Δ xまたはxt−Δ xを作成し、xtの次の値の候補x'とする。どちらにするかは等確率とする
を求める(これは次の値としてx'を採用する確率となる)
- 0〜1の間の乱数rを作る
- r ≤ αなら、新しい候補を採用し、xt+1=x'とする
- そうでなければ、今回の値xtをそのまま使い、xt+1=xtとする
- そのようにして得られた値を記録する
- 上記を繰り返す
これだけだとイメージが湧きにくいかもしれませんが、以下の図で考えると分かりやすいでしょう。これについては解説の動画も用意しました。ぜひとも視聴ください。
動画3 MCMC(メトロポリス法)
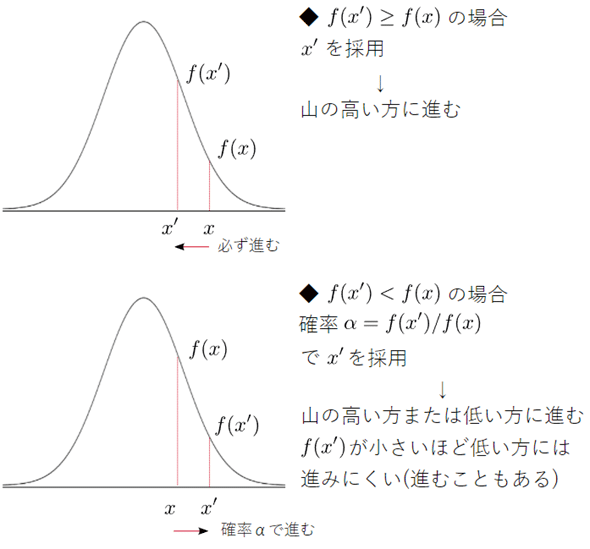
図9 メトロポリス法の考え方
次の候補f(x')の方が大きいときにはαは必ず1になるので、x'が 必ず採用される。つまり、山の高い方に進む。逆に、次の候補f(x')の方が小さいときにはαは1未満になる。その場合は、確率αでx'を採用するので、山の高い方に進むこともあれば、低い方に進むこともある。
図9からも分かるように、標準正規分布の場合であれば、平均値に近い値が多く採用され、平均値から離れた値はより少なく採用されることになります。f(x')が小さいとαも小さくなるので、山の低い方の値が採用される確率も小さくなるというわけです。
というわけで、xtの初期値を0、Δ xを-0.5〜0.5の一様乱数として、作成された値のリストを返す関数metroを作成してください。繰り返し数nは関数metroの引数として与え、metroの返り値を使ってヒストグラムも作成してみましょう(リスト26)。実行例は図10のようになります。
import matplotlib.pyplot as plt
import numpy as np
data = metro(100000) # 関数metroを使って標準正規分布のデータを作成
# ヒストグラムの作成
plt.hist(data, bins=100, density=True)
# 標準正規分布のグラフを重ねる
xrange = np.arange(-6, 6, 0.01)
y = [stdnorm(x) for x in xrange]
plt.plot(xrange, y)
plt.show()
ここでは、10万回の繰り返しにしてみた。関数metroを作成しておけば、このコードを実行することにより図10のグラフが描ける。
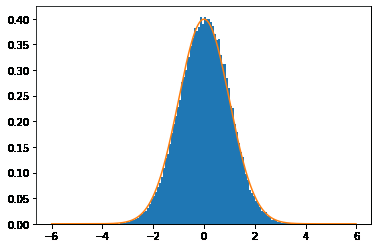
図10 メトロポリス法を使って描いた標準正規分布のグラフ
作成されたデータを基に描画したヒストグラムと対象の関数を使って描画したグラフがほぼ重なっていることが分かる。単純なモンテカルロ法で描いた図7(前ページに掲載)と比べるとかなりスムーズになっている。
なお、この場合は平均値が0であることがあらかじめ分かっているので、初期値を0としましたが、平均値が分からない場合にはランダムな値からスタートすることになります。そのため、結果が安定しない最初の部分(例えば1000個分)はデータを捨てるのが普通です。また、xtの前後には相関(自己相関)があるので、その影響を排除するために何回かに1回、データを記録するのが一般的です。例えば、10回に1回だけデータを記録するなどの方法が取られます。ただし、ここでは、全てのデータを記録するものとします(従ってサンプリングされるデータの個数は、10万回の繰り返しであれば10万個となります。図10のヒストグラムがスムーズなのはそのためです)。
練習問題の解答例
以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではりません。
(1)台形公式とシンプソンの公式で標準正規分布の累積確率を求める
サンプルプログラムの関数integral(1ページ目のリスト2:刻み値を指定する方法)と関数simpson(2ページ目のリスト10)に、標準正規分布を表す関数stdnormの参照と、下限値、上限値、刻み値を与えるだけで求められます。新たに関数を作成する必要はありません。
print(integral(stdnorm, -2, 2, 0.001))
# 出力例:0.9544997181067352
print(simpson(stdnorm, -2, 2, 0.001))
# 出力例:0.9544997361036403
小数点以下15桁まで正確に求めた値は0.954499736103642なので、シンプソンの公式の方が精度が良いことが分かる。
結果は、
- 台形公式: 0.9544997181067352
- シンプソンの公式: 0.9544997361036403
- 正確な値: 0.954499736103642
となり、シンプソンの公式の方がより良い近似値を求められることが分かります。
(2)曲線の長さを求める
微小なΔxの値を刻み値hで表せばリスト2のようなコードが書けます。関数linelengthに与える引数funcには任意の関数が指定できます。
def derivative(f, x, h):
return (f(x+h) - f(x)) / h
def parabolic(x):
return x**2
def linelength(func, xmin, xmax, h):
length = 0
for x in np.arange(xmin, xmax, h):
length += np.sqrt(h**2 + (h * derivative(func, x, h))**2)
return length
hが底辺、h * derivative(func, x, h)が高さなので、ピタゴラスの定理を使って斜辺の長さを求め、それらを全て足し合わせた。
リスト28と前掲のリスト24の実行結果は問題のところに記した通り(1.4789428567991607)です。正確な値(1.4789428575445974...)と、小数点以下8桁まで一致することが分かります。
(3)マルコフ連鎖モンテカルロ法により標準正規分布のサンプリングを行う
これも問題文で記したアルゴリズムをそのままコードとして記述するだけです。次の候補xnextを使った関数の値が、現在の値xを使った関数の値よりも大きければ、alphaは必ず1になります(実際のところ、1以上であればいいのでmin関数を使ってわざわざ1にしなくてもいいのですが)。その場合はxnextを採用します。
xnextを使った関数の値が、現在の値xを使った関数の値よりも小さければ、確率alphaで次の候補を採用します。alphaは、新しい候補を採用するか、現在の値を使うかを表す「閾値」(いきち)であると考えれば分かりやすいと思います。0〜1の乱数rを作って、それがalpha以下であればxnextを採用します(確率alphaでxnextが採用されます)。rがalphaを超えるとxをそのまま次の値として使うというわけです(確率1−alphaでxが採用されます)。これについては、コードの後に図解を入れておきます。
import numpy as np
def stdnorm(x):
return 12*np.pi) * np.exp(-(x**22))
def metro(n):
np.random.seed(0)
x = 0 # 初期値
data = [] # 作成された値
for i in range(n):
xnext = x + np.random.uniform(-0.5, 0.5) # 次の値の候補
alpha = min(1, stdnorm(xnext) / stdnorm(x)) # 次の値の候補を採用する確率α
r = np.random.random()
# rがα以下ならxnextを次の値とする(確率αで次の値となる)
# そうでなければ何もしない(確率1-αで今回の値をそのまま次の値とする)
if r <= alpha:
x = xnext
data.append(x)
return data
stdnorm(xnext)がstdnorm(x)より大きければ、alphaは必ず1となるので、xnextが採用される。alphaが1未満の場合は、確率alphaでxnextが採用される。
リスト29と前掲のリスト26の実行例は問題のところで見た通りです。リスト29では、確率alphaで次の候補を採用する、という部分が少し分かりにくいかもしれないので、以下に図解を掲載しておきます。リスト29と併せて見ておいてください。
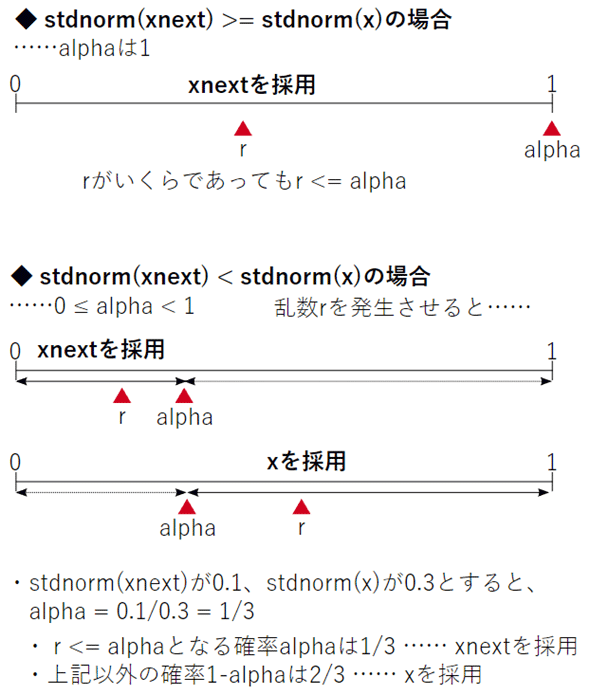
図11 次の候補を採用するかどうかの判定方法
alphaを閾値として、rがalpha以下であればxnextを採用する。この場合、確率alphaでxnextが採用される。そうでなければxを採用する。その確率は1−alphaとなる。stdnorm(xnext)が小さいほどalphaが小さくなるので、xnextが採用される確率は小さくなる。
さらに、作成されたデータを基に、−nσ〜nσ(n=1〜5)の累積確率を求めてみましょう(リスト30)。標準正規分布ではσが1なので、 −n ≤ x < nとなるデータの個数で求められます。リスト29とリスト26がすでに実行されており、作成されたデータがdataに記録されているものとします。
x = np.array(data)
for sigma in range(1, 6):
print(np.count_nonzero((-sigma <= x) & (x < sigma)) / len(x))
# 出力例:
0.6916
0.95867
0.99816
1.0
1.0
この例では、全ての値が−4σ〜4σの範囲内に収まっており、その範囲外のサンプルは作成されていないことが分かる。ちなみに、正確な値は、−1σ〜1σから−5σ〜5σまでの順に0.6826895、0.9544997、0.9973002、0.9999367、0.9999994。
今回は、積分に関する数値計算の方法として、台形公式やシンプソンの公式による近似計算や、乱数を使ったモンテカルロ法による近似計算を学びました。さらに、練習問題では、マルコフ連鎖モンテカルロ法にも少し踏み込んでみました。
次回は少しアルゴリズムに重きをおいて、「再帰をマスターする」をテーマとしたいと思います。再帰に対して多くの人が持つ苦手意識を払拭(ふっしょく)する内容にしたいと思います。動的計画法などについても触れる予定です。
Copyright© Digital Advantage Corp. All Rights Reserved.