［数学×Python］再帰呼び出しをマスターしよう：数学×Pythonプログラミング入門（3/4 ページ）

再帰に対して多くの人が持つであろう苦手意識を払拭（ふっしょく）するために、再帰の基本から、その考え方とプログラミングの方法を見ていく。動的計画法を利用した最小コストの計算法などについても紹介する。

[羽山博，著]

目標3： 動的計画法を利用して最小のコストを求める

　動的計画法とは、再帰的に関数を呼び出し、その結果を表に記録しておくことによって、効率よく計算を行う方法のことを指します。例えば、最短経路を求める問題や、価値が最大になるように品物を袋に入れる問題（いわゆるナップサック問題）などで最適な解を得るために使われます。

　実は、すでに見たメモ化も動的計画法の一つですが、ここでは、簡単な応用例として、コストの小さい値を選んでいく「緩和」という方法を見ていくことにします。

　先ほどの魔王と勇者にまた登場してもらいましょう。魔王は悪の化身だけあって、簡単には階段を上らせてくれません。階段には罠（わな）が仕掛けられていて、階段を上るときに勇者はダメージを受けます。しかし、魔王と闘う前には、できるだけダメージを小さくしておきたいですよね。というわけで、魔王の待つ玉座までたどり着くためのダメージの最小値を求める、というのがここでの目標になります。

　罠は、以下のようになっているものとします（この問題も、目標2と同様、カエルの飛び石の例など、さまざまな形のものがあります）。

• 階段には0〜4のいずれかの整数が記録されている（n段目の値をd_nと表すことにする）
• 0段目にも値が記録されている
• 階段を上るときにダメージを受ける
• ダメージの量は|d_n−d_n−1|または|d_n−d_n−2|となる

　例えば、階段の0段目に1、1段目に3、2段目に2が記録されている場合に、2段目に上がるには、

• 0段目から1段ずつ上がる
  • 0段目から1段目に上がる：|3−1|＝2
  • 1段目から2段目に上がる：|2−3|＝1、なのでダメージは合計3
• 0段目から2段目に上がる：|2−1|＝1なのでダメージは1

となります。同じ段に上がる場合でも、1段ずつ上がった方が有利な場合と、1段飛ばしで上がった方が有利な場合があるというわけです。階段に記録されている値は乱数を使って作成することにします。ただし、結果が確認しやすいように乱数の種を固定しておきましょう。

　では、プログラミングに取り組んでいきます。目標2のプログラムを変更して、ダメージの最小値を返すようにすればできます。

3. 最小のコストで済ませるためのコードを書く

　再帰にも少し慣れてきたと思いますが、漸化式から考えていきましょう。ただし、厳密に数式で表すのではなく、コードを意識した表し方にします。これについても、問題の考え方を中心に動画で解説しているので、ぜひご視聴ください。

動画3　動的計画法（緩和）の問題の考え方

　n段目に記録されている値をd[n]とし、n段目までのダメージの最小値を返す関数をdamage(n)と表すと、以下のように考えられます。n段目に上がるにはn−1段目かn−2段目にいる必要がある、というのはこれまでと同じですね。

　決まった値は次の2つです。

• 0段目にいるときはダメージを受けない（0を返せばよい）
• 1段目に上がるときには、abs(d[1]-d[0])のダメージを受ける

　n段目とn−1段目、n−2段目の関係は以下の通りです。

• 2段目以降はdamage(n-1)+abs(d[n]-d[n-1])とdamage(n-2)+abs(d[n]-d[n-2])の小さい方をdamage(n)の値とする

　つまり「n−1段目までに受けた最小のダメージに、新たに受けるダメージを加えたもの」と「n−2段目までに受けた最小のダメージに、新たに受けるダメージを加えたもの」の小さい方が、より小さいダメージとなるので、その値を採用するというわけです。

　関数damageは再帰的に複数個呼び出されるので、メモ化は必須です。コードはリスト9の通りです。確実に理解するため、漸化式に従って穴埋めをしてみてください。

import random
def damage_m(n):
  def damage(n):
    if n == 0:
      memo[0] = 0
    elif n == 1:
      memo[1] = abs(d[ア] - d[イ])
    elif memo[n] is not ウ:
      pass
    else:
      memo[n] = min(damage(エ) + abs(d[n] - d[エ]), damage(オ) + abs(d[n] - d[オ]))
    return memo[n]

  random.seed(0)
  d = random.choices(range(0, 5), k=n+1)  # 階段に記録されている値
  memo = [None]*(n+1)
  result = damage(n)
  print(d)
  print(memo)
  return result

リスト9　階段を上るときの最小のダメージを求めるコード
関数damage_mでは、randomモジュールのchoices関数を使って0以上5未満の乱数をn＋1個作成する（変数dとする）。次に、n＋1個のメモmemoを用意しておき、関数damageを呼び出す。関数damageはやはり漸化式をそのまま表現したものになっている。ここでは、return文を最後に1つだけ書くようにした。pass文は「何もせずif文を抜ける」という意味。

　コードに難しいところはないと思いますが、関数damageは、関数damage_mの関数内関数であることを確認しておいてください。従って、関数damage_m内で定義されたdやmemoは、関数damageの中でそのまま使えます。

（答え）オレンジ色の部分をクリックすると答えが表示されます。

• ア. 　1　
• イ. 　0　（アとイの順序は逆でも可）
• ウ. 　None　
• エ. 　n-1　
• オ. 　n-2　（エとオの順序は逆でも可）

　では、実行してみましょう（リスト10）。

damage_m(13)
# 出力例：
# [4, 3, 2, 1, 2, 2, 3, 1, 2, 2, 4, 2, 1, 3]  # ダメージの値の一覧
# [0, 1, 2, 3, 2, 2, 3, 3, 4, 4, 6, 4, 5, 5]  # メモの内容(各段の最小ダメージ)
# 5  # 関数damage_mの返り値

リスト10　最小のダメージを求めるコードの実行例
13段の階段を上るときに、罠から受ける最小のダメージは5であることが分かった。実行の様子が分かるように、階段に記録されている値のリストdと、各段に上がるときのダメージのメモmemoも表示するようにした。

　リスト10で出力されたdの値と、memoの値を図にしてみました（図4）。念のため、ダメージの計算方法を再確認しておきましょう。一例として、4段目に上がるときの最小のダメージを求めるための計算を見てみます。

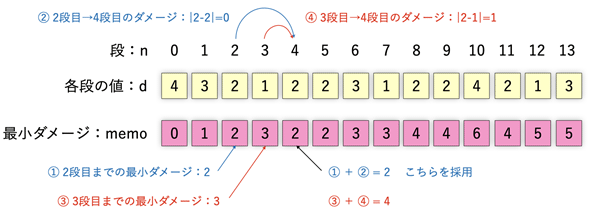
図4　最小のダメージを求める方法
4段目に上がるためには、2段目か3段目にいる必要がある。2段目から上がる場合、（1） 2段目までの最小ダメージは2、（2） 2段目から4段目に上がるときのダメージは|d[4]−d[2]|＝|2−2|＝0なので、この場合のダメージは（1）＋（2）＝2＋0＝2となる。3段目から上がる場合、（3） 3段目までの最小ダメージは3、（2） 3段目から4段目に上がるときのダメージは|d[4]−d[3]|＝|2−1|＝1なので、この場合のダメージは（3）＋（4）＝3＋1＝4となる。従って、4段目に上がるための最小ダメージは2と4の小さい方、つまり2となる。この値がmemo[4]に記録される。

　他の例も穴埋めで考えみてください。例えば、11段目に上がるには、9段目か10段目にいる必要があります。まず、9段目から上がる場合を考えてみましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

• 9段目までの最小ダメージはmemo[9]＝　4　
• 9段目から11段目に上がるときのダメージは
  　|d[11]−d[9]|＝　2　−　2　|＝　0　
• このときのダメージの和は　4　＋　0　＝　4　

　次に10段目から上がる場合です。

• 10段目までの最小ダメージはmemo[10]＝　6　
• 10段目から11段目に上がるときのダメージは
  　|d[11]−d[10]|＝|　2　−　4　|＝　2　
• このときのダメージの和は　6　＋　2　＝　8　

というわけで、memo[11]の値として、小さい方の　4　が採用されます。