［数学×Python］再帰呼び出しをマスターしよう：数学×Pythonプログラミング入門（2/4 ページ）

再帰に対して多くの人が持つであろう苦手意識を払拭（ふっしょく）するために、再帰の基本から、その考え方とプログラミングの方法を見ていく。動的計画法を利用した最小コストの計算法などについても紹介する。

[羽山博，著]

目標2： メモ化により計算量を減らす

　再帰呼び出しを行う関数では、同じ関数を複数呼び出すと計算量が爆発的に増えてしまいます（目標1で見た例では、1つの関数しか呼び出していないので問題ありません）。ちょっと違った例で見てみましょう。

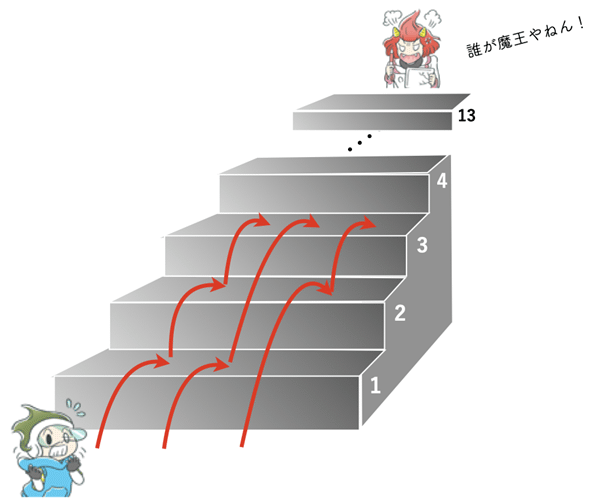
　あなたが魔王の城にたどり着いた勇者だとします（図2）。階段の上の玉座にいる魔王が「我と闘いたくば、この階段を1つずつ、あるいは1つ飛ばしで上る方法は何通りあるかを答えよ」という問いを発してきました。階段は13段あるものとして、この答えを求めるための漸化式とプログラムを書いてみましょう。

図2　階段を上がる方法
階段を1つずつ、あるいは1つ飛ばしで上がる方法。例えば、3段目に上がるには図に示したような3通りの方法がある。階段は全部で13段ある。

　答えを先に言うと377通りなのですが、この例では、再帰を使ったコードを素直に書くと、同じ関数が何度も呼び出され、計算量が大きくなりすぎて使い物になりません（後で見ます）。というわけで、ここでの目標はメモ化という方法を使って計算量を減らすことです。

　メモ化とは、答えがまだ求められていない場合は、関数を呼び出して答えを求め、その値を記録（メモ）しておくことです。次に同じ関数を呼び出そうとしたとき、すでに答えが求められているのであれば、関数を呼び出す代わりに、メモしておいた答えを返すようにするというわけです。まず、メモ化を行わない場合に起こるトラブルから見ていきましょう。

2. メモ化により計算量を減らすコードを書く

　最初に、計算量のことは考えず、素直に漸化式を立ててコードを書いてみます。ここでは階段の上り方の問題にしましたが、同じ考え方の問題として、池の飛び石を1つずつ、あるいは1つ飛ばしでジャンプするカエルの問題など、さまざまな変種があります。漸化式を立てる方法は、

• 初期値などの決まった値がいくらであるかを考える
• n回目の値をn−1回目から求める方法を調べる

でしたね。ここでは、n−1回目だけでなくn−2回目を調べる必要もあります。では、上の方法に従って考えていきましょう。問題の考え方については動画でも解説しているので、ぜひご視聴ください。

動画2　階段を1つずつ、または1つ飛ばしで上がる場合の数

　決まった値は次の2つです。

• 1段目に上がる方法は1通り。1段上がるだけなのでこれしかない
• 2段目に上がる方法は2通り。1段ずつ上がる方法か、2段（1つ飛ばしで）上がる方法のいずれか

　ちょっと悩むのは3段目以降です。ここで、n段目とそれ以前の関係を考えます。n段目に上がるにはn−1段目から上がるか、n−2段目から上がるかのいずれかです。ということは、

• n段目に上がる方法 = （n−1段目に上がる方法の数）+（n−2段目に上がる方法の数）

で求められるはずです。これで漸化式ができます。まとめて書いてみましょう。n段目に上がる方法の数をf(n)とすると、

と表されます。漸化式を立てるには、あくまでもn回目とそれ以前（n−1回目、n−2回目……）の関係のみを考えるのがコツです。具体的に方法を列挙して考えようとするとかえって混乱してしまいます。*3

*3　図2からも分かるように、3段目に上がるための方法を1回で何段上がるかの組み合わせとして列挙すると、{1,1,1},{1,2},{2,1}の3通りになります。4段目に上がる方法は、{1,1,1,1},{1,1,2},{1,2,1},{2,1,1},{2,2}の5通りです。その先を列挙しようとするとちょっと気が遠くなりそうですね。というわけで、3段目に上がるには、その前に1段目にいるか2段目にいる必要があるので、1通り＋2通り＝3通りと考えた方が簡単です。同様に、4段目に上がるにはその前に2段目か3段目にいる必要があるので、2通り＋3通り＝5通りと考えられます。

　では、コードを書いてみましょう。関数名はstairsとします。nが0以下の場合や整数でない場合は考えないことにして、素直に書いてみるとリスト4のようになります。

def stairs(n):
  if n == 1 or n == 2:
    return n
  else:
    return stairs(n-1) + stairs(n-2)

リスト4　階段を上がる方法が何通りあるかを再帰的に求める関数stairsの定義
この例では、n＝1とn＝2の場合に値が決まる。それ以外の場合はn−1段目かn−2段目から上がってくると考えればよい。しかし、このままだと1つのstairs関数から2つのstairs関数を呼び出すことになるので、nが大きくなると計算量が急激に増大する。

　では、実行してみましょう（リスト5）。

stairs(13)
# 377

リスト5　関数stairsを呼び出し、13段目まで上がる方法が何通りあるかを求める
結果は377通りとなる。n＝13程度であればすぐに答えが返ってくる。

　nの値とstairs(n)の値を表にしてみると表2のようになります。この表の値に見覚えはないでしょうか。実は、stairs(n)の値はフィボナッチの数列（の一部分）になっています。

n	1	2	3	4	5	6	7	8	9	10	11	12	13
stairs(n)	1	2	3	5	8	13	21	34	55	89	144	233	377

表2　階段の上り方はフィボナッチの数列で表される
フィボナッチの数列（0,1,1,2,3,5,8,13,...）は、2つ前の値と1つ前の値を足したもの。関数stairsも同じ計算を行っていることに気づくはず。

　関数stairsはnの値が大きくなると急激に計算量が増えます。そのため、Google Colabでは、サーバーに負荷を掛けるので30以上の大きな値を指定して実行するのは絶対にやめるようにしてください。筆者のローカルな環境（iMac2020 27inch、3.3GHz 6コアIntel Corei5、メモリ40GB）では、n＝30で約0.15秒、n＝40で約17秒かかりました。さらに、n＝50ではいくら待っても答えが返ってこないので実行を中断しました。

　理由は簡単です。1つのstairs関数から2つのstairs関数が呼び出され、それぞれがさらに2つのstairs関数を呼び出すので（図3）、おおざっぱに見積もって2ⁿに比例する時間がかかることになるからです。例えば、1秒間に1000億回（10¹¹）回の計算ができるものとすると、

• n=30の場合、2³⁰/10¹¹ ≈ 0.01秒
• n=40の場合、2⁴⁰/10¹¹ ≈ 11.00秒
• n=50の場合、2⁵⁰/10¹¹ ≈ 11259秒=約3.1時間

かかることになります。

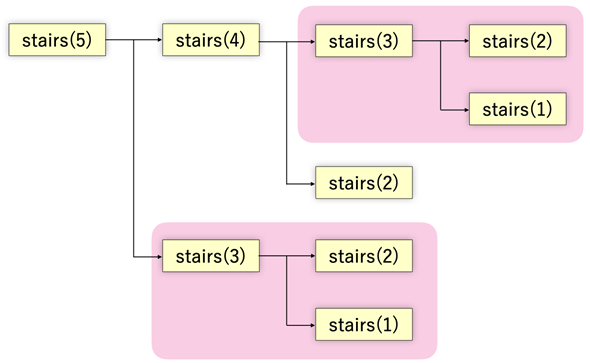
図3　関数stairsは2つの関数stairsを呼び出す
1つの関数から複数の関数を再帰呼び出しすると、同じ関数が何度も呼び出されることが分かる。呼び出し回数は、ざっくりと見積もって2ⁿに比例する。実際には値が決まる場合は関数を呼び出さないので、もう少し小さな値となるが、2ⁿに比べると極めて小さいので、爆発的に計算量が増えることには変わりない。

　図3を見ると、同じ関数が何度も呼び出されていることに気が付きます。例えば、stairs(5)からはstairs(4)とstairs(3)が呼び出されます。stairs(4)からは、またstairs(3)が呼び出されます。それぞれのstairs(3)からはstairs(2)とstairs(1)が呼び出されます。これでは、あまりにもムダが多すぎます。

　そこで、メモ化を使います。答えがまだ求められていない場合は、関数を呼び出して答えを求め、その値を記録しておくということでしたね。すでに答えが求められているのであれば、関数を呼び出さず、メモしておいた答えを返すようにします。そうすれば、何度も同じ関数を呼び出すことがなくなります。コードはリスト6の通りです（もっと簡潔に書く方法もありますが、それについては後述します）。

def stairs_m(n):
  memo = [None]*(n+1)
  return stairs_sub(n, memo)

def stairs_sub(n, memo):
  if n <= 2:
    return n
  elif memo[n] is not None:  # すでに値が求められているのでそれを返す
    return memo[n]
  else:  # まだ値が求められていないので再帰呼び出しを行い、値をメモする
    memo[n] = stairs_sub(n-2, memo) + stairs_sub(n-1, memo)
    return memo[n]

リスト6　メモ化により計算量を減らす
関数stairs_mで、nまでの値を記録しておくために、n＋1個のリストを用意しておき、全ての要素をNoneにしておく。リストの要素がNoneである場合は、答えがまだ求められていないということになる。関数stairs_subでは、memoに値が存在すれば（Noneでなければ）その値を返し、値が存在しなければ、漸化式に従って再帰呼び出しを行う。

　リストの個数をn＋1個にしているのは、nの値とリストのインデックスをそろえるためです。前掲の表2を見ても分かるように、nは1から始まります。そこで、memo[0]は使わないことにして、memo[1]からmemo[n]までに値を記録することにしました。そのためn＋1個の要素を用意しておいたというわけです*4。

*4　*演算子を使うと、同じ値を複数個含むリストを作成できます。この書き方は1次元のリストであれば特に問題は起こりませんが、2次元のリストを作成する場合には注意が必要です。例えば、5行4列のリストを作るために、memo=[[None]*4]*5と書いてしまうと、全ての行が同じ列を参照するようになってしまいます。そのため、例えばmemo[0][1] = 10のような代入を行うとmemo[1][1]やmemo[2][1]などの、1列目の値が全て10になります。2次元のリストを作成する際にはリスト内包表記を使うのが簡単です。リスト内包表記は本連載第5回「Pythonでグラフを描こう ― 棒グラフ／ヒストグラム／散布図／ヒートマップ」でも紹介しました。後の練習問題でも登場します。

　このようにすれば、nの値が大きくなっても計算時間は掛かりません（計算量はnに比例する値となります）。では、n＝100を指定して実行してみましょう（リスト7）。すぐに答えが返ってくるはずです。

stairs_m(100)
# 出力例：573147844013817084101

リスト7　メモ化した関数の実行例
計算量はnに比例するので、大きな値を指定してもすぐに答えが返ってくる。ただし、余りにも大きい値を指定すると、呼び出しの階層が深くなりすぎてスタックがオーバーフローしてしまうので注意。

　なお、リスト6のstairs_sub関数をstairs_m関数の中で定義しておけば、memoを引数として渡す必要がなくなります。リスト8の例では、コードを簡潔にするためにstairs_subの名前をstairsに変更しておきました。

def stairs_m(n):
  def stairs(n):
    if n <= 2:
      return n
    elif memo[n] is not None:
      return memo[n]
    else:
      memo[n] = stairs(n-2) + stairs(n-1)
      return memo[n]

  memo = [None]*(n+1)
  return stairs(n)

リスト8　関数内関数を使ってコードを簡単にする
stairs_m関数で作成されたリストmemoは、stairsでも使えるので、引数として渡す必要がない。

　このように、関数の中で関数を定義することを、そのままのネーミングですが「関数内関数」と呼びます。実行結果はリスト7と同じです。