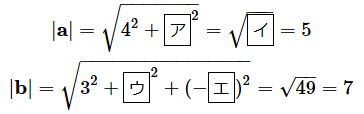Pythonで線形代数！ 〜ベクトル編〜：数学×Pythonプログラミング入門（2/5 ページ）

AI／機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回はベクトルを中心に、その考え方や各種計算のプログラミング方法を初歩から見ていく。

[羽山博，著]

目標2： ベクトルの大きさ

　ベクトルの大きさ（長さ）は、|a|のようにベクトルを|で囲んで表し、以下のように計算されます。

のとき、

　では、a＝(4, 3)やa＝(3, 2, −6)の大きさを求めるコードを書いてみてください。（1）式に従って繰り返し処理を書いて計算しても構いませんが、ここでは、numpy.linag.norm関数を使ってみましょう。引数にベクトルを指定するだけで答えが求められます。

2. ベクトルの大きさを求める

　numpy.linag.norm関数を使ってベクトルの大きさを求めた例はリスト8の通りです。

import numpy as np
import numpy.linalg as LA

a = np.array([4, 3])
b = np.array([3, 2, -6])

print(LA.norm(a))
print(LA.norm(b))
# 出力例：
# 5.0
# 7.0

リスト8　ベクトルの大きさを求めるコードと実行例
numpy.linagモジュールには線形代数の計算のためのさまざまな関数がまとめられている。norm関数では、ベクトルや行列のノルムを求めることができる。ノルムは「大きさ」を表すものと考えてよい（コラムで後述）。

　リスト8で既に答えが求められていますが、計算方法をしっかり確認するために、手計算でもやってみましょう。穴埋めになっているので、aとbの値を（1）式に当てはめて下の式を完成させてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

（答え： ［ア］＝　3　、［イ］＝　25　、［ウ］＝　2　、［エ］＝　6　）

　参考として、繰り返し処理を使って書いた例も見ておきましょう。リスト9の関数L2normのようになります。関数L2normの引数にベクトルを指定すれば答えが求められます。

import numpy as np

def L2norm(vector):
  ssum = 0
  for x in vector:
    ssum += x**2
  return np.sqrt(ssum)

print(L2norm(a))  # リスト8で作成したa=(4, 3)を指定
print(L2norm(b))  # リスト8で作成したb=(3, 2, -6)を指定
# 出力例：
# 5.0
# 7.0

リスト9　ベクトルの大きさを求めるコードと実行例（繰り返し処理を使う）
（1）式の定義通りに関数L2normを書いた例。何次元のベクトルであっても、大きさが計算できる。

　繰り返し処理を使ってコードを書くと、計算の方法を一つ一つ確認できるので、数式の理解が助けられますが、既に数式の意味や計算方法が分かっているなら、目的に合った関数を使った方が効率的です。というわけで、これ以降、便利な関数が用意されている場合には、わざわざ自分で繰り返し処理を書くことは避け、関数を利用することにします（ただし、数式の理解を助けるために、手計算での練習は適宜含めます）。

コラム　ベクトルの大きさにはいろいろな計算方法がある

　ベクトルの大きさは‖x‖のように‖で囲んで表されることもあります。これは、大きさを表す一般的な概念であるノルムを意味します。ノルムとは、

• ‖x‖≥0 で、‖x‖＝0 ⟺ x＝0
• ‖ax‖＝|a|‖x‖ （ただし、|a|はスカラーaの絶対値)
• ‖x‖＋‖y‖≥‖x＋y‖

という条件を満たしているものとして定義されます。つまり、この条件を満たしていれば、どんな計算方法でも「大きさ」と見なせるわけです。

　普通は、（1）式で求められるユークリッド距離（L²ノルム）がよく使われますが、マンハッタン距離（L¹ノルム）などが使われることもあります。マンハッタン距離は|x₁|＋|x₂|＋…＋|x_n|で求められます。どのような方法で決められるノルムであるかは、右下に数字などを書いて表します。例えば、‖x‖₁はxのL¹ノルムを表します。

　numpy.linag.norm関数では、引数ordを省略するか2を指定するとL²ノルムが求められ、1を指定するとL¹ノルムが求められます（リスト10）。

import numpy as np
import numpy.linalg as LA

a = np.array([4, 3])
b = np.array([3, 2, -6])

print(LA.norm(a, ord=1))
print(LA.norm(b, ord=1))
# 出力例：
# 7.0
# 11.0

リスト10　L¹ノルムを求めた例
‖a‖₁＝|4|＋|3|＝7、‖b‖₁＝|3|＋|2|＋|−6|＝11なので、正しい答えが求められていることが分かる。