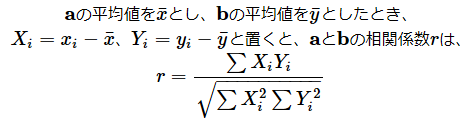Pythonで線形代数！ 〜ベクトル編〜：数学×Pythonプログラミング入門（3/5 ページ）

AI／機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回はベクトルを中心に、その考え方や各種計算のプログラミング方法を初歩から見ていく。

[羽山博，著]

目標3： ベクトルの要素ごとの積と内積

　続いて、ベクトルの要素ごとの積と内積について見てみましょう。

のとき、要素ごとの積と内積は表1のように計算します*3。

表1　ベクトルの要素ごとの積と内積を求める方法
要素ごとの積の計算には*演算子を使い、内積の計算にはinner関数、dot関数または@演算子を使う。ベクトルの内積は、対応する要素の積を全て足したもの。行列の計算ではinner関数の働きと、dot関数や@演算子の働きが異なるので注意が必要だが、ベクトルの場合は全て同じ結果となる（詳細は次回説明する）。

*3　要素ごとの積はアダマール積とも呼ばれます。ここでは⊗という記号で表していますが、°を使うこともあります。なお、×は「外積」と呼ばれる計算の記号として使われます。外積については後述します。

　では、a＝(2,3)、b＝(4,1)とし、要素ごとの積と内積をそれぞれ求めるコードを書いてみてください。

3. ベクトルの要素ごとの積と内積を求める

　利用する演算子がもう分かっているので、コードを書いてしまいましょう。まず、ベクトルの要素ごとの積です。これは*演算子を使います。以下の通りです。

import numpy as np

a = np.array([2, 3])
b = np.array([4, 1])

print(a * b)
# 出力例：
# [8, 3]

リスト11　ベクトルの要素ごとの積を求める
aの最初の要素である2とbの最初の要素である4を掛け、aの次の要素である3とbの最初の要素である1を掛けたベクトルが求められる。

　要素ごとの積を求めると、同じ位置の要素同士を掛け合わせたベクトルが返されます。簡単ですね。

　続いて、内積です。こちらも演算子が分かっているので、内積がどのようなものだったかを忘れてしまっていても、コードは書けます。内積の意味については後で補足することにします。

print(np.inner(a, b))  # リスト11で作成したaとb
print(np.dot(a, b))
print(a @ b)
# 出力例：
# 11
# 11
# 11

リスト12　ベクトルの内積を求める
ベクトルの内積を求めるには、numpyモジュールのinner関数やdot関数に2つのベクトルを指定するか、@演算子を使って計算するかすればよい。ベクトルの場合、いずれも同じ結果になる。

　ところで、目標のところに記した数式をよく見ると、要素ごとの積を全て足した結果が内積になっていることが分かります。従って、print(sum(a * b))またはprint((a * b).sum())でも内積が求められます。しかし、この方法は、ベクトルであればうまくいくのですが、次回取り組む行列ではうまくいきません。ベクトルの場合は、numpyモジュールのinner関数、dot関数または@演算子を使えば簡単に内積が求められるので、これらの関数や演算子を使うといいでしょう。

　では、内積についてのおさらいです。まずは計算方法からです。リスト12で既に答えが求められていますが、手計算で確認しておきましょう。穴埋めになっているので、aとbの値を表1の式に当てはめて下の式を完成させてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

（答え： ［ア］＝　4　、［イ］＝　3　、［ウ］＝　8　、［エ］＝　3　）

　続いて、内積の定義などについて見ていきます。これについては、解説動画で図形的な理解も含めてゆっくりと解説しているので、数式を追いかけるのが苦手な方は、動画をぜひご視聴ください。

動画2　ベクトルの内積

　まずは定義からです。aとbのなす角度をθとしたとき、aとbの内積a ⋅ bは以下のように定義できます。

　|a|は、aの大きさを表します。従って、a ≠ 0かつb ≠ 0の場合には、

となります。また、a⋅b＝0の場合、cosθ＝0となるので、aとbが直交することが分かります。

　内積は、目標の表1にも示したように、成分（要素）ごとの計算によって、

と定義することもできます。また、（1）式で見たように、

なので、（2）式の右辺に（3）式と（4）式を代入すると、2つのベクトルのcosθは、

で計算できます。この値は、ベクトルのコサイン類似度とも呼ばれます（「AI・機械学習の数学入門： ベクトルの基本と類似度の計算」を参照）。

また、

と表されます。これは上で示したcosθの計算方法と全く同じです。X_iとY_iを元に戻すと、

となります。相関係数とは、各データと平均値との差を要素とする2つのベクトルのなす角度にほかなりません。

　話は少しそれますが、この連載の第2回の練習問題では繰り返し処理の練習のために、共分散を求めたり、それを基に相関係数を求めたりしました。実は、共分散を求める関数や相関係数を求める関数はNumPyに用意されています。例えば、aを気温のデータとし、bをビールの売上本数とし、それらを、

という2つのベクトルで表すなら、リスト13のように計算できます。

import numpy as np

a = np.array([12.1, 15.3, 18.6, 21.7, 26.1, 32.1])
b = np.array([45, 520, 2864, 6874, 25487, 102870])

print(np.cov(a, b, bias=True))
print(np.corrcoef(a, b))
# 出力例：
# [[4.45280556e+01 2.11454233e+05]
#  [2.11454233e+05 1.34718638e+09]]
# [[1.         0.86334758]
#  [0.86334758 1.        ]]

リスト13　共分散や相関係数を簡単に求める
cov関数は分散共分散行列を求める関数。4.45280556e+01がaの分散、1.34718638e+09がbの分散、2.11454233e+05がaとbの共分散となっている。bias=Trueを指定すると標本分散と標本共分散が求められる（biasを省略するかFalseを指定すると不偏分散と不偏共分散が求められる。corrcoefは相関行列を求める関数。0.86334758がaとbの相関係数。