Pythonで線形代数! 〜ベクトル編〜:数学×Pythonプログラミング入門(5/5 ページ)
AI/機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回はベクトルを中心に、その考え方や各種計算のプログラミング方法を初歩から見ていく。
練習問題
では、練習問題に取り組みましょう。ここでは、ベクトルの計算に使う関数の利用と、簡単な応用例を取り上げます。問題の考え方について解説した動画も用意してあります。問題を図形的に理解したい方は、ぜひご視聴ください。
動画3 ベクトルの練習問題
(1)ある点と直線や平面との距離を求める
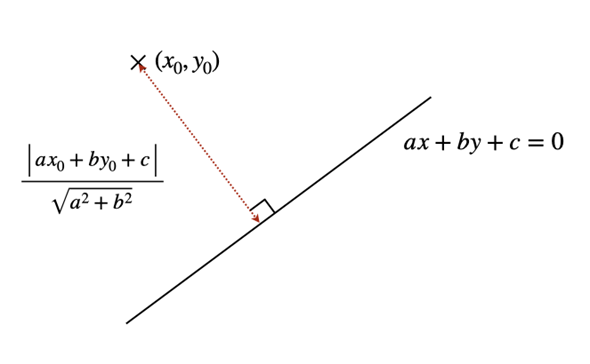
平面上の点(x0, y0)から、直線ax + by + c = 0へ下した垂線の長さは、その点と直線の距離(最短距離)を表します。その長さは、
で求められます(図6)。
また、空間上の点(x0,y0,z0)から、平面ax+by+cz+d=0までの距離も、同様に、
で求められます。
そこで、点の座標を表すベクトルをpという変数名で表し、直線の係数の並びをベクトルと見なしてLという変数で表したときに、距離の計算を行うコードを1行で書いてみてください。
(ヒント1)
平面上の点の座標を(x0, y0)としたとき、これをp=(x0, y0, 1)というベクトルで表してみましょう。直線Lについては、係数の並びをベクトルとして表せばいいので、L=(a, b, c)とします。
(ヒント2)
NumPyの配列でも、リストと同様のスライス機能が使えます。
import numpy as np
import numpy.linalg as LA
p = np.array([1,3,1])
L = np.array([2,1,5])
print( ) # ()の中に距離の計算を行うコードを書く
# 出力例:
# 4.47213595499958
点(1,3)と直線2x+y+5=0との距離は4.47213595499958となる。点の座標を基に、p=(x0, y0, 1)と表せば、簡単な計算だけで点と直線との距離が求められる。()に入るコードを1行で書こう。
ちなみに、ある点と直線(や平面)との距離を求める計算は、判別分析と呼ばれる統計的な手法などで使われます。また、機械学習の一種であるサポートベクターマシンの最も単純な方法は、境界線とそれに最も近い点との距離(マージン)が最大になるように、境界線を定めるというものです。
(2)ニューロンの活動をシミュレートする
以下の図7のように、ニューロンxn−1〜xn+1の信号が、ynに入力されるものとします。このとき、xn−1とxn+1からの信号はynに対して抑制的に働き、xnからの信号はynに対して促進的に働くものとします。例えば、抑制率が0.1の場合、xn−1とxn+1からの信号に-0.1という重みを掛けた値がynに入力されるものとします。xnからの信号に関しては、そのままynに入力されるものとしましょう。その場合、重みは1となります。
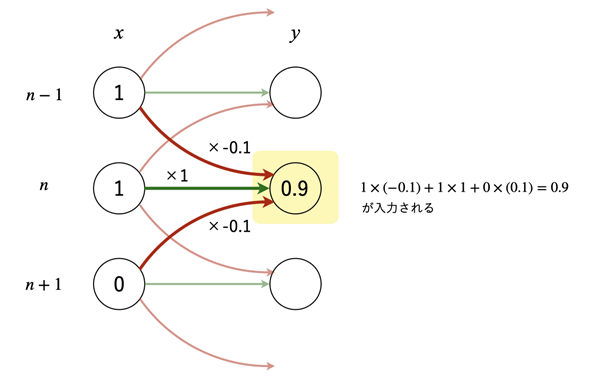
図7 隣り合うニューロンが抑制的に働く場合の入力値を得る
黄色のアミカケをしたニューロンに注目すると、抑制率が0.1の場合、1つ上のニューロンからの信号は抑制的に働くので、1×(−0.1)が入力される。同じ位置のニューロンからの信号は促進的に(そのまま)伝達されるので1×1が入力される。1つ下のニューロンからの信号は抑制的に働くので0×(−0.1)が入力される。合計すると0.9となる。
このとき、x=(x0, x1, ...,xn)に対して、重みw=(w1,w2,w3)を順に適用し、yに入力される値を求める関数inhibitを作成してみてください。なお、プログラムを簡単にするためにy0とynは使わず、返り値としてy1〜yn−1を返すものとします。実行例はリスト17の通りです。返された値を表示するとともに、グレースケール画像として表示し(図8)、値の大小を可視化しておきましょう。
x = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
w = np.array([-0.1, 1, -0.1])
result = inhibit(x, w) # この関数inhibitを作成する
print(result)
plt.imshow([result], cmap='gray')
plt.show()
# 実行例
# [ 0.8 0.8 0.8 0.9 -0.1 0. 0. ]
例えば、y[1] = x[0]*w[0]+x[1]*w[1]+x[2]*w[2]となり、y[2]=x[1]*w[0]+x[2]*w[1]+x[3]*w[2]となる。yのインデックスとxのインデックスの対応を考え、繰り返し処理を使ってinhibit関数を書くとよい。
図8 入力された信号の値をグレースケール画像として表示する
関数inhibitを完成させ、リスト17を実行するとこのような画像が表示される。値を光の強さとすれば、明るい部分(0.8)と黒い部分(0)の境界に、より明るい部分(0.9)とより暗い部分(-0.1)が現れることが分かる。
このようなニューロンの働きを側抑制と呼びます。側抑制はカブトガニの視神経で発見された現象で、輪郭の知覚の生理学的な基礎となっていると言われています(グレースケール画像を見ると明るい色と暗い色の境目である3の部分がより明るく、4の部分がより暗く表示されていることが分かります)。
練習問題の解答例
以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではありません。
(1)ある点と直線や平面との距離を求める
p=(x0, y0, 1)、L=(a, b, c)とするなら、|ax0+by0+c|は、pとLの内積の絶対値であることが分かります。
一方、分母の
の方は、L=(a, b, c)の最後の要素を取り除いたベクトル(a, b)の大きさです。従って、リスト18のようなコードが書けます。
import numpy as np
import numpy.linalg as LA
p = np.array([1,3,1])
L = np.array([2,1,5])
print(abs(p@L)/LA.norm(L[0:-1]))
# 実行例
# 4.47213595499958
@は内積を求めるための演算子。-1というインデックスは最後の要素を意味するので、L[0:-1]は、先頭の要素から、最後の要素の手前まで、という意味になる。
numpy.linalg.norm関数を使わず、print関数をprint(abs(p@L)/np.sqrt(sum(L[0:-1]**2)))と書き、ベクトルの大きさを定義通りに計算してももちろん同じ結果になります。
ある点と平面の距離もリスト18のコードだけで求められます。その場合は、点の座標を基にp=(x0, y0, z0, 1)と表し、L=(a, b, c, d)と表すだけです(平面をLという変数名で表すのは違和感がありますが)。
(2)ニューロンの活動をシミュレートする
入力元のニューロンをx、重みをwというベクトルで表し、重み付けされた値がyというベクトルに入力されるとすると、y[i]に入力される値はx[i-1]*w[i-1]+x[i]*w[i]+x[i+1]*w[i+1]で求められます。これは、xとwの内積にほかなりません。yはxと同じ要素数とし、初期値として0を与えておきます。そして、y[1]〜y[len(y)-2]の値を求めていけば答えが得られます。
import numpy as np
import matplotlib.pyplot as plt
def inhibit(x, w):
y = np.zeros(len(x))
for i in range(1, len(y)-1): # len(y)-1未満まで
y[i] = np.inner(x[i-1:i+2], w)
return y[1:-1]
# ここにリスト17のコードを記述する
numpyモジュールのzeros関数を使えば、ゼロベクトル(全ての要素が0のベクトル)が作れる。内積はdot関数や@演算子で求めてもいいが、ここではinner関数を使った。
AI/機械学習には線形代数の知識を利用したプログラミングが必要不可欠です。今回はそのための基礎としてベクトルの取り扱いについて見てきましたが、計算をより簡潔に表し、コードを簡単にするためには行列の知識とNumPyによる配列の扱いが必須です。
次回は、行列の考え方と基本的な演算の方法、行列の変形(行数と列数の変更、行列の併合/抽出など)について見ていくこととします。
Copyright© Digital Advantage Corp. All Rights Reserved.