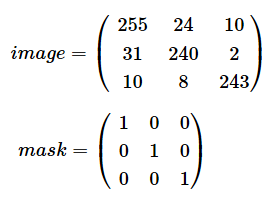Pythonで線形代数！～行列編（基礎・前編）：数学×Pythonプログラミング入門（2/5 ページ）

AI・機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の各種計算や行、列の抽出、形状の変更方法などについて、プログラミングの方法を初歩から見ていく。

[羽山博，著] PC用表示関連情報

LINE

Hatena

前のページへ | 次のページへ

目標2：配列同士の四則演算を行う

　次の目標は、配列同士の四則演算です。目標1で取り扱ったデータを使って以下のような計算を行ってみましょう。

Aの0行0列目に10を加え、1行0列目に20を加え、1行1列目に100を加えた配列を求める

なので、答えは、

になるはずです。

2. 配列同士の四則演算を行うコード

　形の同じ（行と列の要素数が同じ）配列同士であれば、四則演算などの計算は配列の要素ごとに行われます。従って、目標2の計算を行うには、個々の要素に対して個別に計算を行うのではなく、以下のリスト4に示すBのような配列（Aと同じ形の配列）を作っておき、A+Bを求めるのが簡単です。

import numpy as np

A = np.array([[379.7, 350.7, 1154.4],
             [284.6, 269.2, 771.3]])
B = np.array([[10,   0, 0],
              [20, 100, 0]])

print(A + B)
# 出力例：
# [[ 389.7 350.7 1154.4]
# [ 304.6 369.2 771.3]]

リスト4　配列同士の四則演算を行う
A+Bとすると、配列Aの各要素と配列Bの対応する要素を加えて作成された配列が返される。A-Bなら、配列Aの各要素から配列Bの対応する要素を引いて作成された配列が返される。

　いちいち繰り返し処理を使って1つずつ要素を足したりしなくていいので、コードが簡潔に書けますね。

　では、次に進みましょう。……と言いたいところですが、消化不良になる恐れがあるので、確実に理解を進めるために、簡単な練習問題を挟んでおきましょう。

　以下のような配列imageと配列maskについて、それぞれの要素の積を求め、それらの平均値を求めてみてください。要素ごとの積を求めるには*演算子が使えます。また、meanメソッドを使うと配列の要素全ての平均値が求められます。

　すぐ下に作成例がありますが、まずはそれを見ずに取り組んでみてください。なお、maskを左右反転させた配列を使って計算した例についてもコードに含めてあります。

import numpy as np

image = np.array([[255, 24, 10],
[31, 240, 2],
[10, 8, 243]])
mask = np.eye(3) # 3行3列の単位行列を作る

print((image * mask).mean())
print((image * np.fliplr(mask)).mean()) # maskを左右反転
# 出力例：
# 82.0 # この値と次の値の意味は後述
# 28.88888888888889

リスト5　配列同士の要素ごとの積で作成された配列の平均値を求める
maskについては、各要素が0と1からなる3×3の配列として表してもいいが、単位行列を作成するeye関数を使って表した。それぞれの行列を配列として表し、*演算子でつなげば要素ごとの積を求めた配列が返される。その平均値をmeanメソッドで求めればよい。fliplr関数は配列を左右に反転させる関数。

　配列maskは、行位置と列位置が等しい要素（対角要素）が全て1で、他の部分が0となっています。このような配列で表される行列のことを単位行列と呼びます。単位行列を作成するには、eye関数やidentity関数が使えます。引数には行数と列数を表す値を指定します*2。

*2　単位行列は行数と列数が同じなので、引数は1つ指定するだけで構いません。しかし、eye関数では、単位行列を行数と列数が異なる配列にして返したり、行や列をずらした配列にして返したりすることもできます。詳細については、NumPy公式マニュアル「numpy.eye」などを参照してください。

　実は、リスト5の例は、畳み込みニューラルネットワークの畳み込み層を求めるのに使われる計算と似たものになっています。配列maskは「＼」のような斜線と考えられますね。その部分の値だけが取り出されるので、配列imageに「＼」のような斜線が含まれていれば（実際、配列imageには0行0列目、1行1列目、2行2列目に大きな値が含まれています）、結果は大きな値になります。元画像の全てのデータについて同様の計算をすれば、どこに右肩下がりの斜線が含まれているかを検出できるというわけです。

　リスト5にはNumPyのfliplr関数を使ってmaskを左右反転させた配列（こちらは「／」のような斜線に当たる）を使って同じ計算を行った例も含めてあります。こちらは値が小さいので（実際、配列imageの0行2列目と2行0列目の値は小さくなっています）、imageには「／」のような斜線は含まれないと考えられます。

コラム　配列に対してReLU関数を適用する

　次の目標3では、配列とベクトルのブロードキャストや、配列同士のブロードキャストの例を紹介しますが、その前に、これまでに見てきた機能を利用した、ちょっと面白い利用例も紹介しておきましょう。以下のリスト6は、ニューラルネットワークの活性化関数としてよく使われるReLU関数と同じ計算を配列に対して一気に適用する例です。ReLU関数は値が0以下の場合には0を、そうでない場合には値そのものを返す関数です。

import numpy as np

cells = np.array([[-0.5, 0.3],
[0.1, -0.8]])

print(cells * (cells > 0))
# 出力例：
# [[-0. 0.3]
# [ 0.1 -0. ]]

リスト6　配列に対してReLU関数を適用する
cells > 0では、配列cellsの各要素が0より大きければTrueとなり、0以下であればFalseとなる配列が返される（ブロードキャスト機能による）。続いて*演算子により、配列cellsと、そのようにして求めた配列の要素ごとの積を求める。従って、配列cellsの各要素が0より大きければ元の値にTrueが掛けられ、0以下であればFalseが掛けられる。数値と真偽値の計算を行う場合、Trueは1、Falseは0と見なされるので、元の値が0より大きければ元の値、0以下であれば0となるような配列が返される。

　リスト6では、cellsは配列にしてありますが、ベクトルでももちろん同じことができます。浮動小数点数では、負の値と0を掛けると-0.0のように表示されますが、これは0.0と考えてもらって構いません。