Pythonで線形代数！〜行列編（基礎・前編）：数学×Pythonプログラミング入門（3/5 ページ）

AI・機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の各種計算や行、列の抽出、形状の変更方法などについて、プログラミングの方法を初歩から見ていく。

[羽山博，著]

目標3： 配列とベクトル、配列同士のブロードキャスト

　NumPyのブロードキャスト機能により、配列の個々の要素に対する四則演算などができることは既に見た通りですが、ブロードキャスト機能は配列とスカラーだけでなく、形が合えば、配列とベクトル、配列と配列の間でも利用できます。

　では、ここでの目標です。目標1で扱ったデータを使い、以下の計算を行ってみてください。

• 全ての行について、0列目に10、1列目に50を足す
• 全ての列について、1行目に10、2行目に20を足す

なので、答えは、前者が、

になり、後者が、

になるはずです。

　なお、配列同士でブロードキャストが行われる例については、ここでの目標としては挙げませんが、配列とベクトルのブロードキャストの例の後で、説明を加えてあります。

3. 配列とベクトル、配列同士のブロードキャストを行うコード

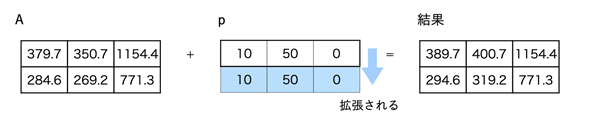
　最初の例から見ていきましょう。これは、配列とベクトルの四則演算になります。3列目には値を足していませんが、0を足すと考えればいいですね。ということで、配列Aの各行に[10, 50, 0]というベクトルを足します。

import numpy as np

A = np.array([[379.7, 350.7, 1154.4],
             [284.6, 269.2,  771.3]])
p = np.array([10, 50, 0])

print(A + p)
# 出力例：
# [[ 389.7  400.7 1154.4]
#  [ 294.6  319.2  771.3]]  # Aの各行に[10, 50, 0]を加えた配列

リスト7　ブロードキャスト機能により配列と行ベクトルの和を求める
配列Aとベクトルpは行数は異なるが列数は同じ。この場合は、ベクトルが行方向（下方向）に拡張され、[[10, 50, 0], [10, 50, 0]]が配列Aに足される。

　リスト7のようにすれば、ブロードキャスト機能により、全ての行にベクトルpの各要素が足されます。どのような計算になるか、図で確認しておきましょう（図1）。以降、図の解説には動画も用意してあるので、ぜひご視聴ください。

動画1　NumPyブロードキャスト機能（配列とベクトルを足す場合）

図1　ブロードキャスト機能により配列と行ベクトルを足す
列数が同じであれば、ベクトルが行方向に（下に）拡張され、各行に足される。

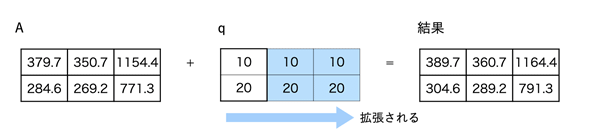
　次の例については以下のリスト8の通りです。こちらも配列とベクトルの四則演算ですが、ベクトルを列ベクトル（n行1列の配列）としています。全ての列にベクトルqの各要素が足されます。

import numpy as np

A = np.array([[379.7, 350.7, 1154.4],
             [284.6, 269.2,  771.3]])
q = np.array([[10],
              [20]])

print(A + q)
# 出力例：
# [[ 389.7  360.7 1164.4]
#  [ 304.6  289.2  791.3]]  # Aの各列に[[10],[20]]を加えた配列

リスト8　ブロードキャスト機能により配列と列ベクトルの和を求める
配列Aとベクトルqは列数は異なるが行数は同じ。この場合は、ベクトルが列方向（右方向）に拡張され、[[10], [20]]が配列Aに足される。

　出力例を見れば、どのような計算が行われているかが分かると思いますが、こちらも図で確認しておきましょう（図2）。ベクトルqは2行1列の配列ですが、列ベクトルと見なせます。

図2　ブロードキャスト機能により行列と列ベクトルを足す
行数が同じであれば、ベクトルが列方向に（右に）拡張され、各行に足される。

　なお、リスト8の例では、q = np.array([10, 20]).reshape((2, 1))としても構いません。reshapeメソッドは行列の形を変えるためのもので、引数に指定した(2, 1)というタプルは、2行1列に変形するという意味です*3。

*3　reshapeメソッドで、行数や列数に-1を指定すると「残りは自動的に計算する」という意味になります。従って、この例であれば(2, -1)と指定することもできます。1行2列の配列を2行に変形するなら、列は1列にしかなり得ないので、-1を指定すれば(2, 1)と見なされる、というわけです。一般に、x行y列の配列を(n, -1)の形に変形すると、(n, x*y/n)の形になります。もちろん、x*y/nは整数でなければいけません。

　さらに、配列同士のブロードキャストについても見てみまみしょう。

　配列同士の四則演算を行う場合、どちらの配列も基本的に同じ形でなければなりません。しかし、一方の配列が他方の配列の中で繰り返される形になっている場合、ブロードキャスト機能により配列を拡張して計算することができます。例えば、配列Aの形が2×3で、配列Bの形が2×3×2×3であれば、配列Aを配列Bに加えることができます。その場合、2×3行列が繰り返し足されることになります。実行例の後で図解を掲載してあるので、コード（リスト9）と図解（図3）を見ながらどのような計算になっているか確認してみてください。

import numpy as np

A = np.arange(2*3).reshape(2,3)
B = np.arange(2*3*2*3).reshape(2,3,2,3)

print(A)
# 出力例：
#  [[0 1 2]
#  [3 4 5]]

print(B)
#  [[[[ 0  1  2]
#    [ 3  4  5]]
#
#   [[ 6  7  8]
#    [ 9 10 11]]
#
#   [[12 13 14]
#    [15 16 17]]]
#
#
#  [[[18 19 20]
#    [21 22 23]]
#
#   [[24 25 26]
#    [27 28 29]]
#
#   [[30 31 32]
#    [33 34 35]]]]

print(A+B)
#  [[[[ 0  2  4]
#    [ 6  8 10]]
#
#   [[ 6  8 10]
#    [12 14 16]]
#
#   [[12 14 16]
#    [18 20 22]]]
#
#
#  [[[18 20 22]
#    [24 26 28]]
#
#   [[24 26 28]
#    [30 32 34]]
#
#   [[30 32 34]
#    [36 38 40]]]]

リスト9　ブロードキャスト機能を利用して配列を繰り返し加える
NumPyのarange関数を使って、0以上6（＝2*3）未満の等差数列を1次元の配列として作り、それをreshapeメソッドで2×3の形に変形し、Aとする。Bは0以上36（＝2*3*2*3）未満の配列をreshapeメソッドで2×3×2×3の形にしたもの。A+Bとすれば、配列Aが繰り返し配列Bに加えられる。

　以下の図解については、穴埋め問題にしておきましょう。ア〜カに入る値は幾らになるでしょう。簡単なルールなので、すぐに分かると思います。リスト9の実行結果を見ずにやった後、リスト8と照らし合わせてみてください。

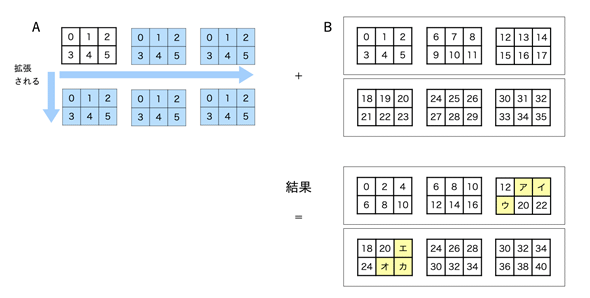
図3　配列同士のブロードキャスト
一方の配列の形が、他方の配列の最後の部分のインデックスの形と同じ行数、列数になっていれば、配列が拡張され、それぞれ足されていく。上の例以外でも、3 × 2 × 3の配列と、2 × 3 × 3 × 2 × 3の配列であれば、ブロードキャスト機能を利用した足し算などができる（太字の部分が同じ形になっていることに注目）。

（答え）
　［ア］＝　14　、［イ］＝　16　、［ウ］＝　18　、
　［エ］＝　22　、［オ］＝　26　、［カ］＝　28　

　配列Bは四次元の配列なので、イメージするのが難しいかもしれませんね。例えば、配列Bの中の31という値は、大きな枠の1つ目、その並びの2つ目の配列、その中の0行目、その中の1列目なので、B[1, 2, 0, 1]となります。後述のコラム「行方向／列方向と軸について」で説明している「軸」を意識すれば、もう少しスッキリすると思います。